Affine combination
Encyclopedia
In mathematics
, an affine combination of vectors x1, ..., xn is a vector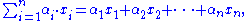
called a linear combination
of x1, ..., xn , in which the sum of the coefficients is 1, thus:
Here the vectors are elements of a given vector space
V over a field
K, and the coefficients
are scalars
in K.
This concept is important, for example, in Euclidean geometry
.
The act of taking an affine combination commutes with any affine transformation
T in the sense that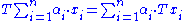
In particular, any affine combination of the fixed point
s of a given affine transformation
is also a fixed point of 
, so the set of fixed points of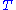 
forms an affine subspace (in 3D: a line or a plane, and the trivial cases, a point or the whole space).
When a stochastic matrix
, A, acts on a column vector, B, the result is a column vector whose entries are affine combinations of B with coefficients from the rows in A.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an affine combination of vectors x1, ..., xn is a vector
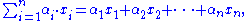
called a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of x1, ..., xn , in which the sum of the coefficients is 1, thus:
Here the vectors are elements of a given vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, and the coefficients
are scalarsScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
in K.
This concept is important, for example, in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
.
The act of taking an affine combination commutes with any affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
T in the sense that
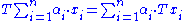
In particular, any affine combination of the fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of a given affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
is also a fixed point of , so the set of fixed points of 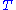forms an affine subspace (in 3D: a line or a plane, and the trivial cases, a point or the whole space).When a stochastic matrix
Stochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
, A, acts on a column vector, B, the result is a column vector whose entries are affine combinations of B with coefficients from the rows in A.
Related combinations
- Convex combinationConvex combinationIn convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
- Conical combinationConical combinationGiven a finite number of vectors x_1, x_2, \dots, x_n\, in a real vector space, a conical combination or a conical sum of these vectors is a vector of the formwhere the real numbers \alpha_i\, satisfy \alpha_i\ge 0...
- Linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...