Scalar (mathematics)
Encyclopedia
In linear algebra
, real number
s are called scalars and relate to vectors in a vector space
through the operation of scalar multiplication
, in which a vector can be multiplied by a number to produce another vector.
More generally, a vector space may be defined by using any field
instead of real numbers, such as complex number
s. Then the scalars of that vector space will be the elements of the associated field.
Also, a scalar product operation (not to be confused with scalar multiplication
) may be defined on a vector space, allowing two vectors to be multiplied to produce a scalar. A vector space equipped with a scalar product is called an inner product space
.
The real component of a quaternion
is also called its scalar part.
The term is also sometimes used informally to mean a vector, matrix
, tensor
, or other usually "compound" value that is actually reduced to a single component. Thus, for example, the product of a 1×n matrix and an n×1 matrix, which is formally a 1×1 matrix, is often said to be a scalar.
The term scalar matrix is used to denote a matrix of the form kI where k is a scalar and I is the identity matrix
.
the first recorded usage of the term was by W. R. Hamilton
in 1846, to refer to the real part of a quaternion
:
is defined as a set of vectors, a set of scalars, and a scalar multiplication
operation that takes a scalar k and a vector v to another vector kv. For example, in a coordinate space
, the scalar multiplication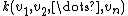
yields 
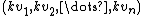. In a (linear) function space
, kƒ is the function x k(ƒ(x)).
The scalars can be taken from any field, including the rational
, algebraic
, real, and complex numbers, as well as finite field
s.
. It follows that every vector space over a scalar field K is isomorphic
to a coordinate vector space where the coordinates are elements of K. For example, every real vector space of dimension
n is isomorphic to n-dimensional real space Rn.
function that assigns to every vector v in V a scalar ||v||. By definition, multiplying v by a scalar k also multiplies its norm by |k|. If ||v|| is interpreted as the length of v, this operation can be described as scaling the length of v by k. A vector space equipped with a norm is called a normed vector space
(or normed linear space).
The norm is usually defined to be an element of V' s scalar field K, which restricts the latter to fields that support the notion of sign. Moreover, if V has dimension 2 or more, K must be closed under square root, as well as the four arithmetic operations; thus the rational numbers Q are excluded, but the surd field is acceptable. For this reason, not every scalar product space is a normed vector space.
(so that, for example, the division of scalars need not be defined), the resulting more general algebraic structure is called a module
.
In this case the "scalars" may be complicated objects. For instance, if R is a ring, the vectors of the product space Rn can be made into a module with the n×n matrices with entries from R as the scalars. Another example comes from manifold theory
, where the space of sections
of the tangent bundle
forms a module over the algebra
of real functions on the manifold.
, a kind of linear transformation
.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s are called scalars and relate to vectors in a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
through the operation of scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
, in which a vector can be multiplied by a number to produce another vector.
More generally, a vector space may be defined by using any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
instead of real numbers, such as complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. Then the scalars of that vector space will be the elements of the associated field.
Also, a scalar product operation (not to be confused with scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
) may be defined on a vector space, allowing two vectors to be multiplied to produce a scalar. A vector space equipped with a scalar product is called an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
.
The real component of a quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
is also called its scalar part.
The term is also sometimes used informally to mean a vector, matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, or other usually "compound" value that is actually reduced to a single component. Thus, for example, the product of a 1×n matrix and an n×1 matrix, which is formally a 1×1 matrix, is often said to be a scalar.
The term scalar matrix is used to denote a matrix of the form kI where k is a scalar and I is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
Etymology
The word scalar derives from the English word "scale" for a range of numbers, which in turn is derived from scala (Latin for "ladder"). According to a citation in the Oxford English DictionaryOxford English Dictionary
The Oxford English Dictionary , published by the Oxford University Press, is the self-styled premier dictionary of the English language. Two fully bound print editions of the OED have been published under its current name, in 1928 and 1989. The first edition was published in twelve volumes , and...
the first recorded usage of the term was by W. R. Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in 1846, to refer to the real part of a quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
:
- The algebraically real part may receive, according to the question in which it occurs, all values contained on the one scale of progression of numbers from negative to positive infinity; we shall call it therefore the scalar part.
Scalars of vector spaces
A vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is defined as a set of vectors, a set of scalars, and a scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
operation that takes a scalar k and a vector v to another vector kv. For example, in a coordinate space
Coordinate space
In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.-Definition:...
, the scalar multiplication
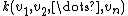yields 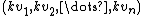. In a (linear) function spaceFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
, kƒ is the function x k(ƒ(x)).
The scalars can be taken from any field, including the rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
, algebraic
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
, real, and complex numbers, as well as finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s.
Scalars as vector components
According to a fundamental theorem of linear algebra, every vector space has a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
. It follows that every vector space over a scalar field K is isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to a coordinate vector space where the coordinates are elements of K. For example, every real vector space of dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
n is isomorphic to n-dimensional real space Rn.
Scalars in normed vector spaces
Alternatively, a vector space V can be equipped with a normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
function that assigns to every vector v in V a scalar ||v||. By definition, multiplying v by a scalar k also multiplies its norm by |k|. If ||v|| is interpreted as the length of v, this operation can be described as scaling the length of v by k. A vector space equipped with a norm is called a normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
(or normed linear space).
The norm is usually defined to be an element of V
Scalars in modules
When the requirement that the set of scalars form a field is relaxed so that it need only form a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
(so that, for example, the division of scalars need not be defined), the resulting more general algebraic structure is called a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
.
In this case the "scalars" may be complicated objects. For instance, if R is a ring, the vectors of the product space Rn can be made into a module with the n×n matrices with entries from R as the scalars. Another example comes from manifold theory
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, where the space of sections
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
forms a module over the algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
of real functions on the manifold.
Scaling transformation
The scalar multiplication of vector spaces and modules is a special case of scalingScaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
, a kind of linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
.
Scalar operations (computer science)
Operations that apply to a single value at a time.- Scalar processorScalar processorScalar processors represent the simplest class of computer processors. A scalar processor processes one datum at a time . , a scalar processor is classified as a SISD processor .In a vector processor, by contrast, a single instruction operates simultaneously on multiple data items...