Tensor
Encyclopedia
Tensors are geometric
objects that describe linear relations between vectors, scalars
, and other tensors. Elementary examples include the dot product
, the cross product
, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of numerical values. The order (also degree or rank) of a tensor is the dimensionality of the array needed to represent it, or equivalently, the number of indices needed to label a component of that array. For example, a linear map can be represented by a matrix, a 2-dimensional array, and therefore is a 2nd-order tensor. A vector can be represented as a 1-dimensional array and is a 1st-order tensor. Scalars are single numbers and are thus zeroth-order tensors.
Tensors are used to represent correspondences between sets of geometrical vectors. For example, the stress tensor T takes a direction v as input and produces the stress T(v) on the surface normal to this vector as output and so expresses a relationship between these two vectors. Because they express a relationship between vectors, tensors themselves must be independent of a particular choice of coordinate system
. Taking a coordinate basis or frame of reference
and applying the tensor to it results in an organized multidimensional array representing the tensor in that basis, or as it looks from that frame of reference. The coordinate independence of a tensor then takes the form of a "covariant" transformation law
that relates the array computed in one coordinate system to that computed in another one. This transformation law is considered to be built in to the notion of a tensor in a geometrical or physical setting, and the precise form of the transformation law determines the type (or valence) of the tensor.
Tensors are important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as elasticity, fluid mechanics, and general relativity. Tensors were first conceived by Tullio Levi-Civita
and Gregorio Ricci-Curbastro
, who continued the earlier work of Bernhard Riemann
and Elwin Bruno Christoffel
and others, as part of the absolute differential calculus. The concept enabled an alternative formulation of the intrinsic differential geometry of a manifold
in the form of the Riemann curvature tensor
.
to describe something different from what is now meant by a tensor.Namely, the norm operation
in a certain type of algebraic system (now known as a Clifford algebra
). The contemporary usage was brought in by Woldemar Voigt
in 1898.
Tensor calculus was developed around 1890 by Gregorio Ricci-Curbastro
(also called just Ricci) under the title absolute differential calculus, and originally presented by Ricci in 1892. It was made accessible to many mathematicians by the publication of Ricci and Tullio Levi-Civita
's 1900 classic text Méthodes de calcul différentiel absolu et leurs applications (Methods of absolute differential calculus and their applications).
In the 20th century, the subject came to be known as tensor analysis, and achieved broader acceptance with the introduction of Einstein
's theory of general relativity
, around 1915. General relativity is formulated completely in the language of tensors. Einstein had learned about them, with great difficulty, from the geometer Marcel Grossmann
. Levi-Civita then initiated a correspondence with Einstein to correct mistakes Einstein had made in his use of tensor analysis. The correspondence lasted 1915–17, and was characterized by mutual respect, with Einstein at one point writing:
Tensors were also found to be useful in other fields such as continuum mechanics
. Some well-known examples of tensors in differential geometry are quadratic form
s such as metric tensor
s, and the Riemann curvature tensor
. The exterior algebra
of Hermann Grassmann
, from the middle of the nineteenth century, is itself a tensor theory, and highly geometric, but it was some time before it was seen, with the theory of differential form
s, as naturally unified with tensor calculus. The work of Élie Cartan
made differential forms one of the basic kinds of tensor fields used in mathematics.
From about the 1920s onwards, it was realised that tensors play a basic role in algebraic topology
(for example in the Künneth theorem
). Correspondingly there are types of tensors at work in many branches of abstract algebra
, particularly in homological algebra
and representation theory
. Multilinear algebra can be developed in greater generality than for scalars coming from a field
, but the theory is then certainly less geometric, and computations more technical and less algorithmic. Tensors are generalized within category theory
by means of the concept of monoidal category
, from the 1960s.
Just like the components of a vector change when we change the basis
of the vector space, the entries of a tensor also change under such a transformation. Each tensor comes equipped with a transformation law that details how the components of the tensor respond to a change of basis. The components of a vector can respond in two distinct ways to a change of basis (see covariance and contravariance of vectors),
where R is a matrix and in the second expression the summation sign was suppressed (a notational convenience introduced by Einstein that will be used throughout this article). The components, vi, of a regular (or column) vector, v, transform with the inverse of the matrix R,
where the hat denotes the components in the new basis. While the components, wi, of a covector or (row vector), w transform with the matrix R itself,
The components of a tensor transform in a similar manner with a transformation matrix for each index. If an index transforms like a vector with the inverse of the basis transformation, it is called contravariant and is traditionally denoted with an upper index, while an index that transforms with the basis transformation itself is called covariant and is denoted with a lower index. The transformation law for a rank m tensor with n contravariant indices and m−n covariant indices is thus given as,
Such a tensor is said to be of order or type .There is a plethora of different terminology for this around. The terms order, type, rank, valence, and degree are in use for the same concept. This article uses the term "order" or "total order" for the total dimension of the array (or its generalisation in other definitions) m in the preceding example, and the term type for the pair giving the number contravariant and covariant indices. A tensor of type will also be referred to as a "" tensor for short.
This discussion motivates the following formal definition:
The definition of a tensor as a multidimensional array satisfying a transformation law traces back to the work of Ricci. Nowadays, this definition is still used in physics and engineering text books.
, but they are often simply referred to as tensors themselves.
In this context the defining transformation law takes a different form. The "basis" for the tensor field is determined by the coordinates of the underlying space, and the defining transformation law is expressed in terms of partial derivative
s of the coordinate functions,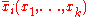
, defining a coordinate transformation,
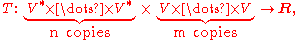
where V is a vector space
and V* is the corresponding dual space
of covectors, which is linear in each of its arguments.
By applying a multilinear map T of type (n,m) to a basis {ej} for V and a canonical cobasis {εi} for V*,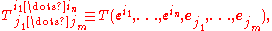
a n+m dimensional array of components can be obtained. A different choice of basis will yield different components. But, because T is linear in all of its arguments, the components satisfy the tensor transformation law used in the multilinear array definition. The multidimensional array of components of T thus form a tensor according to that definition. Moreover, such an array can be realised as the components of some multilinear map T. This motivates viewing multilinear maps as the intrinsic objects underlying tensors.
This approach, defining tensors as multilinear maps, is used in modern differential geometry textbooks and more mathematically inclined physics textbooks.
s of vector spaces, which in turn are defined through a universal property
. A type (n,m) tensor is defined in this context as an element of the tensor product of vector spaces,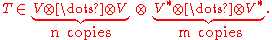
If vi is a basis of V and wj is a basis of W, then the tensor product
has a natural basis 
. The components of a tensor T are the coefficients of the tensor with respect to the basis obtained from a basis {ei} for V and its dual {εj}, i.e.
Using the properties of the tensor product, it can be shown that these components satisfy the transformation law for a type (m,n) tensor. Moreover, the universal property of the tensor product gives a 1-to-1 correspondence
between tensors defined in this way and tensors defined as multilinear maps.
Raising an index on an (n, m)-tensor produces an (n + 1, m - 1)-tensor; this can be visualized as moving diagonally up and to the right on the table. Symmetrically, lowering an index can be visualized as moving diagonally down and to the left on the table. Contracting an (n, m)-tensor produces an (n - 1, m - 1)-tensor; this can be visualized as moving diagonally up and to the left on the table.
. On components, these operations are simply performed component for component. These operations do not change the type of the tensor, however there also exist operations that change the type of the tensors.
takes two tensors, S and T, and produces a new tensor, S ⊗ T, whose order is the sum of the orders of the original tensors. When described as multilinear maps, the tensor product simply multiplies the two tensors, i.e.
which again produces a map that is linear in all its arguments. On components the effect similarly is to multiply the components of the two input tensors, i.e.
If S is of type (k,l) and T is of type (n,m), then the tensor product S ⊗ T has type (k+n,l+m).
is an operation that reduces the total order of a tensor by two. More precisely, it reduces a type (n,m) tensor to a type (n-1,m-1) tensor. In terms of components, the operation is achieved by summing over one contravariant and one covariant index of tensor. For example, a (1,1)-tensor Tij can be contracted to a scalar through
.
Where the summation is again implied. When the (1,1)-tensor is interpreted as a linear map, this operation is known as the trace
.
The contraction is often used in conjunction with the tensor product to contract an index from each tensor.
The contraction can also be understood in terms of the definition of a tensor as an element of a tensor product of copies of the space V with the space V* by first decomposing the tensor into a linear combination of simple tensors, and then applying a factor from V* to a factor from V. For example, a tensor
can be written as a linear combination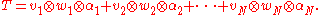
The contraction of T on the first and last slots is then the vector
Conversely, a metric has an inverse which is a (2,0)-tensor. This inverse metric can be contracted with a lower index to produce an upper index. This operation is called raising an index.
or fluid
are described by a tensor. The stress tensor and strain tensor are both second order tensors, and are related in a general linear elastic material by a fourth-order elasticity tensor. In detail, the tensor quantifying stress in a 3-dimensional solid object has components that can be conveniently represented as a 3×3 array. The three faces of a cube-shaped infinitesimal volume segment of the solid are each subject to some given force. The force's vector components are also three in number. Thus, 3×3, or 9 components are required to describe the stress at this cube-shaped infinitesimal segment. Within the bounds of this solid is a whole mass of varying stress quantities, each requiring 9 quantities to describe. Thus, a second order tensor is needed.
If a particular surface element
inside the material is singled out, the material on one side of the surface will apply a force on the other side. In general, this force will not be orthogonal to the surface, but it will depend on the orientation of the surface in a linear manner. This is described by a tensor of type (2,0), in linear elasticity
, or more precisely by a tensor field of type (2,0), since the stresses may vary from point to point.
, with the trifocal tensor
generalizing the fundamental matrix.
The field of nonlinear optics
studies the changes to material polarization density under extreme electric fields. The polarization waves generated are related to the generating electric field
s through the nonlinear susceptibility tensor. If the polarization P is not linearly proportional to the electric field E, the medium is termed nonlinear. To a good approximation (for sufficiently weak fields, assuming no permanent dipole moments are present), P is given by a Taylor series
in E whose coefficients are the nonlinear susceptibilities:
Here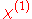
is the linear susceptibility, 
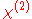gives the Pockels effect
and second harmonic generation
, and
gives the Kerr effect
. This expansion shows the way higher-order tensors arise naturally in the subject matter.
to have a "density". A tensor with density r transforms as an ordinary tensor under coordinate transformations, except that it is also multiplied by the determinant of the Jacobian to the rth power. Invariantly, in the language of multilinear algebra, one can think of tensor densities as multilinear maps taking their values in a density bundle such as the (1-dimensional) space of n-forms (where n is the dimension of the space), as opposed to taking their values in just R. Higher "weights" then just correspond to taking additional tensor products with this space in the range.
In the language of vector bundle
s, the determinant bundle of the tangent bundle
is a line bundle
that can be used to 'twist' other bundles r times. While locally the more general transformation law can indeed be used to recognise these tensors, there is a global question that arises, reflecting that in the transformation law one may write either the Jacobian determinant, or its absolute value. Non-integral powers of the (positive) transition functions of the bundle of densities make sense, so that the weight of a density, in that sense, is not restricted to integer values.
Restricting to changes of coordinates with positive Jacobian determinant is possible on orientable manifolds, because there is a consistent global way to eliminate the minus signs; but otherwise the line bundle of densities and the line bundle of n-forms are distinct. For more on the intrinsic meaning, see density on a manifold
.)
coordinate system, a tensor transforms in a certain way when a rotation is applied. However, there is additional structure to the group of rotations that is not exhibited by the transformation law for tensors: see orientation entanglement
and plate trick
. Mathematically, the rotation group
is not simply connected. Spinor
s are mathematical objects that generalize the transformation law for tensors in a way that is sensitive to this fact.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
objects that describe linear relations between vectors, scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
, and other tensors. Elementary examples include the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of numerical values. The order (also degree or rank) of a tensor is the dimensionality of the array needed to represent it, or equivalently, the number of indices needed to label a component of that array. For example, a linear map can be represented by a matrix, a 2-dimensional array, and therefore is a 2nd-order tensor. A vector can be represented as a 1-dimensional array and is a 1st-order tensor. Scalars are single numbers and are thus zeroth-order tensors.
Tensors are used to represent correspondences between sets of geometrical vectors. For example, the stress tensor T takes a direction v as input and produces the stress T(v) on the surface normal to this vector as output and so expresses a relationship between these two vectors. Because they express a relationship between vectors, tensors themselves must be independent of a particular choice of coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
. Taking a coordinate basis or frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
and applying the tensor to it results in an organized multidimensional array representing the tensor in that basis, or as it looks from that frame of reference. The coordinate independence of a tensor then takes the form of a "covariant" transformation law
Covariant transformation
In physics, a covariant transformation is a rule , that describes how certain physical entities change under a change of coordinate system....
that relates the array computed in one coordinate system to that computed in another one. This transformation law is considered to be built in to the notion of a tensor in a geometrical or physical setting, and the precise form of the transformation law determines the type (or valence) of the tensor.
Tensors are important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as elasticity, fluid mechanics, and general relativity. Tensors were first conceived by Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
and Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro was an Italian mathematician. He was born at Lugo di Romagna. He is most famous as the inventor of the tensor calculus but published important work in many fields....
, who continued the earlier work of Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
and Elwin Bruno Christoffel
Elwin Bruno Christoffel
Elwin Bruno Christoffel was a German mathematician and physicist.-Life:...
and others, as part of the absolute differential calculus. The concept enabled an alternative formulation of the intrinsic differential geometry of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
in the form of the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
.
History
The concepts of later tensor analysis arose from the work of Carl Gauss in differential geometry, and the formulation was much influenced by the theory of algebraic forms and invariants developed in the middle of the nineteenth century. The word "tensor" itself was introduced in 1846 by William Rowan HamiltonWilliam Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
to describe something different from what is now meant by a tensor.Namely, the norm operation
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
in a certain type of algebraic system (now known as a Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
). The contemporary usage was brought in by Woldemar Voigt
Woldemar Voigt
Woldemar Voigt was a German physicist, who taught at the Georg August University of Göttingen. Voigt eventually went on to head the Mathematical Physics Department at Göttingen and was succeeded in 1914 by Peter Debye, who took charge of the theoretical department of the Physical Institute...
in 1898.
Tensor calculus was developed around 1890 by Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro was an Italian mathematician. He was born at Lugo di Romagna. He is most famous as the inventor of the tensor calculus but published important work in many fields....
(also called just Ricci) under the title absolute differential calculus, and originally presented by Ricci in 1892. It was made accessible to many mathematicians by the publication of Ricci and Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
's 1900 classic text Méthodes de calcul différentiel absolu et leurs applications (Methods of absolute differential calculus and their applications).
In the 20th century, the subject came to be known as tensor analysis, and achieved broader acceptance with the introduction of Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, around 1915. General relativity is formulated completely in the language of tensors. Einstein had learned about them, with great difficulty, from the geometer Marcel Grossmann
Marcel Grossmann
Marcel Grossmann was a mathematician of Jewish ancestry, and a friend and classmate of Albert Einstein. He became a Professor of Mathematics at the Federal Polytechnic Institute in Zurich, today the ETH Zurich, specializing in descriptive geometry....
. Levi-Civita then initiated a correspondence with Einstein to correct mistakes Einstein had made in his use of tensor analysis. The correspondence lasted 1915–17, and was characterized by mutual respect, with Einstein at one point writing:
Tensors were also found to be useful in other fields such as continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
. Some well-known examples of tensors in differential geometry are quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s such as metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
s, and the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
. The exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of Hermann Grassmann
Hermann Grassmann
Hermann Günther Grassmann was a German polymath, renowned in his day as a linguist and now also admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher...
, from the middle of the nineteenth century, is itself a tensor theory, and highly geometric, but it was some time before it was seen, with the theory of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s, as naturally unified with tensor calculus. The work of Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
made differential forms one of the basic kinds of tensor fields used in mathematics.
From about the 1920s onwards, it was realised that tensors play a basic role in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
(for example in the Künneth theorem
Künneth theorem
In mathematics, especially in homological algebra and algebraic topology, a Künneth theorem is a statement relating the homology of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology of two topological spaces X and Y and their...
). Correspondingly there are types of tensors at work in many branches of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, particularly in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
. Multilinear algebra can be developed in greater generality than for scalars coming from a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, but the theory is then certainly less geometric, and computations more technical and less algorithmic. Tensors are generalized within category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
by means of the concept of monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
, from the 1960s.
Definition
There are several approaches to defining tensors. Although seemingly different, the approaches just describe the same geometric concept using different languages and at different levels of abstraction.As multidimensional arrays
Just as a scalar is described by a single number, and a vector with respect to a given basis is described by an array, any tensor with respect to a basis is described by a multidimensional array. The numbers in the array are known as the scalar components of the tensor or simply its components. They are denoted by indices giving their position in the array, in sub and superscript, after the name of the tensor. The total number of indices required to uniquely specify each component is equal to the dimension of the array, and is called the order or the rank of the tensor.This article will be using the term order, since the term rank has a different meaning in the related context of matrices. For example, the entries (also called components) of an order 2 tensor T would be denoted Tij, where i and j are indices running from 1 to the dimension of the related vector space.Just like the components of a vector change when we change the basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of the vector space, the entries of a tensor also change under such a transformation. Each tensor comes equipped with a transformation law that details how the components of the tensor respond to a change of basis. The components of a vector can respond in two distinct ways to a change of basis (see covariance and contravariance of vectors),
where R is a matrix and in the second expression the summation sign was suppressed (a notational convenience introduced by Einstein that will be used throughout this article). The components, vi, of a regular (or column) vector, v, transform with the inverse of the matrix R,
where the hat denotes the components in the new basis. While the components, wi, of a covector or (row vector), w transform with the matrix R itself,
The components of a tensor transform in a similar manner with a transformation matrix for each index. If an index transforms like a vector with the inverse of the basis transformation, it is called contravariant and is traditionally denoted with an upper index, while an index that transforms with the basis transformation itself is called covariant and is denoted with a lower index. The transformation law for a rank m tensor with n contravariant indices and m−n covariant indices is thus given as,
Such a tensor is said to be of order or type .There is a plethora of different terminology for this around. The terms order, type, rank, valence, and degree are in use for the same concept. This article uses the term "order" or "total order" for the total dimension of the array (or its generalisation in other definitions) m in the preceding example, and the term type for the pair giving the number contravariant and covariant indices. A tensor of type will also be referred to as a "" tensor for short.
This discussion motivates the following formal definition:
The definition of a tensor as a multidimensional array satisfying a transformation law traces back to the work of Ricci. Nowadays, this definition is still used in physics and engineering text books.
Tensor fields
In many applications, especially in differential geometry and physics, it is natural to consider the components of a tensor to be functions. This was, in fact, the setting of Ricci's original work. In modern mathematical terminology such an object is called a tensor fieldTensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
, but they are often simply referred to as tensors themselves.
In this context the defining transformation law takes a different form. The "basis" for the tensor field is determined by the coordinates of the underlying space, and the defining transformation law is expressed in terms of partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of the coordinate functions,
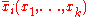, defining a coordinate transformation,As multilinear maps
A downside to the definition of a tensor using the multidimensional array approach is that it is not apparent from the definition that the defined object is indeed basis independent, as is expected from an intrinsically geometric object. Although it is possible to show that transformation laws indeed ensure independence from the basis, sometimes a more intrinsic definition is preferred. One approach is to define a tensor as a multilinear map. In that approach a type (n,m) tensor T is defined as a map,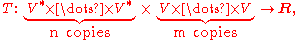where V is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
and V* is the corresponding dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of covectors, which is linear in each of its arguments.
By applying a multilinear map T of type (n,m) to a basis {ej} for V and a canonical cobasis {εi} for V*,
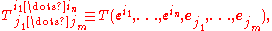
a n+m dimensional array of components can be obtained. A different choice of basis will yield different components. But, because T is linear in all of its arguments, the components satisfy the tensor transformation law used in the multilinear array definition. The multidimensional array of components of T thus form a tensor according to that definition. Moreover, such an array can be realised as the components of some multilinear map T. This motivates viewing multilinear maps as the intrinsic objects underlying tensors.
This approach, defining tensors as multilinear maps, is used in modern differential geometry textbooks and more mathematically inclined physics textbooks.
Using tensor products
For some mathematical applications, a more abstract approach is sometimes useful. This can be achieved by defining tensors in terms of elements of tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of vector spaces, which in turn are defined through a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
. A type (n,m) tensor is defined in this context as an element of the tensor product of vector spaces,
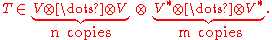
If vi is a basis of V and wj is a basis of W, then the tensor product
has a natural basis . The components of a tensor T are the coefficients of the tensor with respect to the basis obtained from a basis {ei} for V and its dual {εj}, i.e.Using the properties of the tensor product, it can be shown that these components satisfy the transformation law for a type (m,n) tensor. Moreover, the universal property of the tensor product gives a 1-to-1 correspondence
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between tensors defined in this way and tensors defined as multilinear maps.
Examples
This table shows important examples of tensors, including both tensors on vector spaces and tensor fields on manifolds. The tensors are classified according to their type (n, m). For example, a bilinear form is the same thing as a (0, 2)-tensor; an inner product is an example of a (0, 2)-tensor, but not all (0, 2)-tensors are inner products. In the (0, N)-entry of the table, N denotes the dimension of the underlying vector space or manifold.| |n=0 | n=1 | n=2 | ... | |
| m=0 | scalar Scalar (mathematics) In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector.... , e.g. scalar curvature Scalar curvature In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point... |
vector | bivector Bivector In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors... , e.g. inverse metric tensor |
|
| m=1 | covector, linear functional Linear functional In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the... , 1-form |
linear transformation Linear transformation In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0... |
||
| m=2 | bilinear form, e.g. inner product, metric tensor Metric tensor In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean... , Ricci curvature Ricci curvature In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space... , 2-form, symplectic form |
e.g. cross product Cross product In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them... in three dimensions |
e.g. elasticity tensor | |
| m=3 | e.g. 3-form | e.g. Riemann curvature tensor Riemann curvature tensor In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds... |
| | |
| ... | | | |||
| m=N | e.g. N-form i.e. determinant Determinant In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well... , volume form Volume form In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume... |
| | ||
| ... | | |
Raising an index on an (n, m)-tensor produces an (n + 1, m - 1)-tensor; this can be visualized as moving diagonally up and to the right on the table. Symmetrically, lowering an index can be visualized as moving diagonally down and to the left on the table. Contracting an (n, m)-tensor produces an (n - 1, m - 1)-tensor; this can be visualized as moving diagonally up and to the left on the table.
Einstein notation
Einstein notation is a convention for writing tensors that dispenses with writing summation signs by leaving them implicit. It relies on the idea that any repeated index is summed over: if the index i is used twice in a given term of a tensor expression, it means that the values are to be summed over i. Several distinct pairs of indices may be summed this way, but commonly only when each index has the same range, so all the omitted summations are sums from 1 to N for some given N.Abstract index notation
The abstract index notation is a way to write tensors such that the indices are no longer thought of as numerical, but rather are indeterminates. The abstract index notation captures the expressiveness of indices and the basis-independence of index-free notation.Operations
There are a number of basic operations that may be conducted on tensors that again produce a tensor. The linear nature of tensor implies that two tensors of the same type may be added together, and that tensors may be multiplied by a scalar with results analogous to the scaling of a vectorScalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
. On components, these operations are simply performed component for component. These operations do not change the type of the tensor, however there also exist operations that change the type of the tensors.
Tensor product
The tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
takes two tensors, S and T, and produces a new tensor, S ⊗ T, whose order is the sum of the orders of the original tensors. When described as multilinear maps, the tensor product simply multiplies the two tensors, i.e.
which again produces a map that is linear in all its arguments. On components the effect similarly is to multiply the components of the two input tensors, i.e.
If S is of type (k,l) and T is of type (n,m), then the tensor product S ⊗ T has type (k+n,l+m).
Contraction
Tensor contractionTensor contraction
In multilinear algebra, a tensor contraction is an operation on one or more tensors that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor caused by applying the summation...
is an operation that reduces the total order of a tensor by two. More precisely, it reduces a type (n,m) tensor to a type (n-1,m-1) tensor. In terms of components, the operation is achieved by summing over one contravariant and one covariant index of tensor. For example, a (1,1)-tensor Tij can be contracted to a scalar through
.Where the summation is again implied. When the (1,1)-tensor is interpreted as a linear map, this operation is known as the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
.
The contraction is often used in conjunction with the tensor product to contract an index from each tensor.
The contraction can also be understood in terms of the definition of a tensor as an element of a tensor product of copies of the space V with the space V* by first decomposing the tensor into a linear combination of simple tensors, and then applying a factor from V* to a factor from V. For example, a tensor
can be written as a linear combination
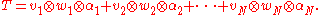
The contraction of T on the first and last slots is then the vector
Raising or lowering an index
When a vector space is equipped with an inner product (or metric as it is often called in this context), there exist operations that convert a contravariant (upper) index into a covariant (lower) index and vice versa. A metric itself is a (symmetric) (0,2)-tensor, it is thus possible to contract an upper index of a tensor with one of lower indices of the metric. This produces a new tensor with the same index structure as the previous, but with lower index in the position of the contracted upper index. This operation is quite graphically known as lowering an index.Conversely, a metric has an inverse which is a (2,0)-tensor. This inverse metric can be contracted with a lower index to produce an upper index. This operation is called raising an index.
Continuum mechanics
Important examples are provided by continuum mechanics. The stresses inside a solid bodySolid body
A solid-body instrument is a string instrument such as a guitar, bass or violin built without its normal sound box and relying on an electric pickup system to directly receive the vibrations of the strings....
or fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
are described by a tensor. The stress tensor and strain tensor are both second order tensors, and are related in a general linear elastic material by a fourth-order elasticity tensor. In detail, the tensor quantifying stress in a 3-dimensional solid object has components that can be conveniently represented as a 3×3 array. The three faces of a cube-shaped infinitesimal volume segment of the solid are each subject to some given force. The force's vector components are also three in number. Thus, 3×3, or 9 components are required to describe the stress at this cube-shaped infinitesimal segment. Within the bounds of this solid is a whole mass of varying stress quantities, each requiring 9 quantities to describe. Thus, a second order tensor is needed.
If a particular surface element
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
inside the material is singled out, the material on one side of the surface will apply a force on the other side. In general, this force will not be orthogonal to the surface, but it will depend on the orientation of the surface in a linear manner. This is described by a tensor of type (2,0), in linear elasticity
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
, or more precisely by a tensor field of type (2,0), since the stresses may vary from point to point.
Other examples from physics
Common applications include- Electromagnetic tensorElectromagnetic tensorThe electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
(or Faraday's tensor) in electromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation... - Finite deformation tensorsFinite deformation tensorsIn continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which both rotations and strains are arbitrarily large, i.e. invalidates the assumptions inherent in infinitesimal strain theory...
for describing deformations and strain tensor for strainStrain (materials science)In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
in continuum mechanicsContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles... - PermittivityPermittivityIn electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
and electric susceptibilityElectric susceptibilityIn electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
are tensors in anisotropic media - Four-tensors in general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
(e.g. stress-energy tensorStress-energy tensorThe stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
), used to represent momentumMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
fluxFluxIn the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
es - Spherical tensor operators are the eigenfunctions of the quantum angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
operator in spherical coordinates - Diffusion tensors, the basis of Diffusion Tensor Imaging, represent rates of diffusion in biologic environments
Applications of tensors of order > 2
The concept of a tensor of order two is often conflated with that of a matrix. Tensors of higher order do however capture ideas important in science and engineering, as has been shown successively in numerous areas as they develop. This happens, for instance, in the field of computer visionComputer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, with the trifocal tensor
Trifocal tensor
In computer vision, the trifocal tensor is a 3×3×3 array of numbers that incorporates all projective geometric relationshipsamong three views...
generalizing the fundamental matrix.
The field of nonlinear optics
Nonlinear optics
Nonlinear optics is the branch of optics that describes the behavior of light in nonlinear media, that is, media in which the dielectric polarization P responds nonlinearly to the electric field E of the light...
studies the changes to material polarization density under extreme electric fields. The polarization waves generated are related to the generating electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
s through the nonlinear susceptibility tensor. If the polarization P is not linearly proportional to the electric field E, the medium is termed nonlinear. To a good approximation (for sufficiently weak fields, assuming no permanent dipole moments are present), P is given by a Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
in E whose coefficients are the nonlinear susceptibilities:
Here
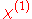is the linear susceptibility, 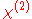gives the Pockels effectPockels effect
The Pockels effect , or Pockels electro-optic effect, produces birefringence in an optical medium induced by a constant or varying electric field. It is distinguished from the Kerr effect by the fact that the birefringence is proportional to the electric field, whereas in the Kerr effect it is...
and second harmonic generation
Second harmonic generation
An optical frequency multiplier is a nonlinear optical device, in which photons interacting with a nonlinear material are effectively "combined" to form new photons with greater energy, and thus higher frequency...
, and
gives the Kerr effectKerr effect
The Kerr effect, also called the quadratic electro-optic effect , is a change in the refractive index of a material in response to an applied electric field. The Kerr effect is distinct from the Pockels effect in that the induced index change is directly proportional to the square of the electric...
. This expansion shows the way higher-order tensors arise naturally in the subject matter.
Tensor densities
It is also possible for a tensor fieldTensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
to have a "density". A tensor with density r transforms as an ordinary tensor under coordinate transformations, except that it is also multiplied by the determinant of the Jacobian to the rth power. Invariantly, in the language of multilinear algebra, one can think of tensor densities as multilinear maps taking their values in a density bundle such as the (1-dimensional) space of n-forms (where n is the dimension of the space), as opposed to taking their values in just R. Higher "weights" then just correspond to taking additional tensor products with this space in the range.
In the language of vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s, the determinant bundle of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
is a line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
that can be used to 'twist' other bundles r times. While locally the more general transformation law can indeed be used to recognise these tensors, there is a global question that arises, reflecting that in the transformation law one may write either the Jacobian determinant, or its absolute value. Non-integral powers of the (positive) transition functions of the bundle of densities make sense, so that the weight of a density, in that sense, is not restricted to integer values.
Restricting to changes of coordinates with positive Jacobian determinant is possible on orientable manifolds, because there is a consistent global way to eliminate the minus signs; but otherwise the line bundle of densities and the line bundle of n-forms are distinct. For more on the intrinsic meaning, see density on a manifold
Density on a manifold
In mathematics, and specifically differential geometry, a density is a spatially varying quantity on a differentiable manifold which can be integrated in an intrinsic manner. Abstractly, a density is a section of a certain trivial line bundle, called the density bundle...
.)
Spinors
Starting with an orthonormalOrthonormality
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal and both of unit length. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length...
coordinate system, a tensor transforms in a certain way when a rotation is applied. However, there is additional structure to the group of rotations that is not exhibited by the transformation law for tensors: see orientation entanglement
Orientation entanglement
In mathematics and physics, the notion of orientation entanglement is sometimes used to develop intuition relating to the geometry of spinors or alternatively as a concrete realization of the failure of the special orthogonal groups to be simply connected....
and plate trick
Plate trick
In mathematics and physics, the plate trick, also known as Feynman's plate trick, Dirac's belt trick, spinor spanner or quaternionic handshake is any of several particular physical demonstrations of the mathematical theorem that SU double-covers SO, or sometimes this fact itself...
. Mathematically, the rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
is not simply connected. Spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s are mathematical objects that generalize the transformation law for tensors in a way that is sensitive to this fact.
Notation
- Voigt notationVoigt notationIn mathematics, Voigt notation or Voigt form in multilinear algebra is a way to represent a symmetric tensor by reducing its order. There are a few variants and associated names for this idea: Mandel notation, Mandel–Voigt notation and Nye notation are others found. Kelvin notation is a revival by...
- Mandel notation
- Penrose graphical notationPenrose graphical notationIn mathematics and physics, Penrose graphical notation or tensor diagram notation is a visual depiction of multilinear functions or tensors proposed by Roger Penrose. A diagram in the notation consists of several shapes linked together by lines, much like tinker toys...
- Raising and lowering indicesRaising and lowering indicesIn mathematics and mathematical physics, given a tensor on a manifold M, in the presence of a nonsingular form on M , one can raise or lower indices: change a type tensor to a tensor or to a tensor...
Foundational
- Fibre bundle
- One-formOne-formIn linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...
- Tensor product of modulesTensor product of modulesIn mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps to be carried out in terms of linear maps...
- Multilinear projection
Applications
- Covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
- Application of tensor theory in engineeringApplication of tensor theory in engineeringTensors are frequently used in engineering to describe measured quantities.-Common applications:* Measuring deformations and strain in continuum mechanics* Representing diffusion as a tensor in Diffusion tensor imaging...
- CurvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
- Diffusion tensor MRI
- Einstein field equationsEinstein field equationsThe Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
- Fluid mechanicsFluid mechanicsFluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
- Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
- Tensor derivative
- Tensor decomposition
- Multilinear subspace learningMultilinear subspace learningMultilinear subspace learning aims to learn a specific small part of a large space of multidimensional objects having a particular desired property. It is a dimensionality reduction approach for finding a low-dimensional representation with certain preferred characteristics of high-dimensional...
- Structure TensorStructure tensorIn mathematics, the structure tensor, also referred to as the second-moment matrix, is a matrix derived from the gradient of a function. It summarizes the predominant directions of the gradient in a specified neighborhood of a point, and the degree to which those directions are coherent...
- Tensor softwareTensor softwareTensor software is a class of mathematical software designed for manipulation and calculation with tensors.-Standalone open-source software:* is a computer algebra system designed specifically for the solution of problems encountered in field theory...
External links
- Introduction to Vectors and Tensors, Vol 1: Linear and Multilinear Algebra by Ray M. Bowen and C. C. Wang.
- Introduction to Vectors and Tensors, Vol 2: Vector and Tensor Analysis by Ray M. Bowen and C. C. Wang.
- An Introduction to Tensors for Students of Physics and Engineering by Joseph C. Kolecki, released by NASANASAThe National Aeronautics and Space Administration is the agency of the United States government that is responsible for the nation's civilian space program and for aeronautics and aerospace research...
- A discussion of the various approaches to teaching tensors, and recommendations of textbooks
- A Quick Introduction to Tensor Analysis by R. A. Sharipov.
- Introduction to Tensors by Joakim Strandberg.