Line bundle
Encyclopedia
In mathematics
, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent
line at each point determines a varying line: the tangent bundle
is a way of organising these. More formally, in algebraic topology
and differential topology
a line bundle is defined as a vector bundle
of rank 1.
There is an evident difference between one-dimensional real line bundles (as just described) and one-dimensional complex
line bundles. In fact the topology of the 1×1 invertible real matrices and complex matrices is entirely different: the first of those is a space homotopy
equivalent to a discrete two-point space
(positive and negative reals contracted down), while the second has the homotopy type of a circle
.
A real line bundle is therefore in the eyes of homotopy theory as good as a fiber bundle
with a two-point fiber - a double covering. This reminds one of the orientable double cover on a differential manifold: indeed that's a special case in which the line bundle is the determinant bundle (top exterior power) of the tangent bundle. The Möbius strip
corresponds to a double cover of the circle (the θ → 2θ mapping) and can be viewed if we wish as having fibre two points, the unit interval
or the real line: the data are equivalent.
In the case of the complex line bundle, we are looking in fact also for circle bundles. There are some celebrated ones, for example the Hopf fibrations of sphere
s to spheres.
. The projectivization P(V) of a vector space V over a field k is defined to be the quotient of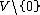
by the action of the multiplicative group k×. Each point of P(V) therefore corresponds to a copy of k×, and these copies of k× can be assembled into a k×-bundle over P(V). k× differs from k only by a single point, and by adjoining that point to each fiber, we get a line bundle on P(V). This line bundle is called the tautological line bundle. This line bundle is sometimes denoted 
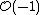since it corresponds to the dual of the Serre twisting sheaf 
.
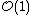Global sections determine maps to projective spaces in the following way: Choosing r + 1 not all zero points in a fiber of L chooses a fiber of the tautological line bundle on Pr, so choosing r + 1 non-simultaneously vanishing global sections of L determines a map from X into projective space Pr. This map sends the fibers of L to the fibers of the dual of the tautological bundle. More specifically, suppose that s0, ..., sr are global sections of L. In a small neighborhood U in X, these sections determine k-valued functions on U whose values depend on the choice of trivialization. However, they are determined up to simultaneous multiplication by a non-zero function, so their ratios are well-defined. That is, over a point x, the values s0(x), ..., sr(x) are not well-defined because a change in trivialization will multiply them each by a non-zero constant λ. But it will multiply them by the same constant λ, so the homogeneous coordinates
[s0(x) : ... : sr(x)] are well-defined as long as the sections s0, ..., sr do not simultaneously vanish at x. Therefore, if the sections never simultaneously vanish, they determine a form [s0 : ... : sr] which gives a map from X to Pr, and the pullback of the dual of the tautological bundle under this map is L. In this way, projective space acquires a universal property
.
The universal way to determine a map to projective space is to map to the projectivization of the vector space of all sections of L. In the topological case, there is a non-vanishing section at every point which can be constructed using a bump function which vanishes outside a small neighborhood of the point. Because of this, the resulting map is defined everywhere. However, the codomain is usually far, far too big to be useful. The opposite is true in the algebraic and holomorphic settings. Here the space of global sections is often finite dimensional, but there may not be any non-vanishing global sections at a given point. In fact, it is possible for a bundle to have no non-zero global sections at all; this is the case for the tautological line bundle.
of a smooth manifold. The resulting determinant bundle is responsible for the phenomenon of tensor densities
, in the sense that for an orientable manifold it has a global section, and its tensor powers with any real exponent may be defined and used to 'twist' any vector bundle by tensor product
.
classifies smooth real line bundles; in particular, the collection of (equivalence classes of) real line bundles are in correspondence with elements of the first cohomology with Z/2Z coefficients; this correspondence is in fact an isomorphism of abelian groups (the group operations being tensor product of line bundles and the usual addition on cohomology). Analogously, the first Chern class
classifies smooth complex line bundles on a space, and the group of line bundles is isomorphic to the second cohomology class with integer coefficients. However, bundles can have equivalent smooth structure
s (and thus the same first Chern class) but different holomorphic structures. The Chern class statements are easily proven using the exponential sequence of sheaves
on the manifold.
One can more generally view the classification problem from a homotopy-theoretic point of view. There is a universal bundle for real line bundles, and a universal bundle for complex line bundles. According to general theory about classifying space
s, the heuristic is to look for contractible spaces on which there are group action
s of the respective groups C2 and S1, that are free actions. Those spaces can serve as the universal principal bundle
s, and the quotients for the actions as the classifying spaces BG. In these cases we can find those explicitly, in the infinite-dimensional analogues of real and complex projective space
.
Therefore the classifying space BC2 is of the homotopy type of RP∞, the real projective space given by an infinite sequence of homogeneous coordinates
. It carries the universal real line bundle; in terms of homotopy theory that means that any real line bundle L on a CW complex
X determines a classifying map from X to RP∞, making L a bundle isomorphic to the pullback of the universal bundle. This classifying map can be used to define the Stiefel-Whitney class of L, in the first cohomology of X with Z/2Z coefficients, from a standard class on RP∞.
In an analogous way, the complex projective space CP carries a universal complex line bundle. In this case classifying maps give rise to the first Chern class
of X, in H2(X) (integral cohomology).
There is a further, analogous theory with quaternion
ic (real dimension four) line bundles. This gives rise to one of the Pontryagin class
es, in real four-dimensional cohomology.
In this way foundational cases for the theory of characteristic class
es depend only on line bundles. According to a general splitting principle
this can determine the rest of the theory (if not explicitly).
There are theories of holomorphic line bundles on complex manifold
s, and invertible sheaves
in algebraic geometry
, that work out a line bundle theory in those areas.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
line at each point determines a varying line: the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
is a way of organising these. More formally, in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
a line bundle is defined as a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
of rank 1.
There is an evident difference between one-dimensional real line bundles (as just described) and one-dimensional complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
line bundles. In fact the topology of the 1×1 invertible real matrices and complex matrices is entirely different: the first of those is a space homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
equivalent to a discrete two-point space
Discrete two-point space
In topology, a branch of mathematics, a discrete two-point space is the simplest example of a totally disconnected discrete space. The points can be denoted by the symbols 0 and 1....
(positive and negative reals contracted down), while the second has the homotopy type of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
.
A real line bundle is therefore in the eyes of homotopy theory as good as a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
with a two-point fiber - a double covering. This reminds one of the orientable double cover on a differential manifold: indeed that's a special case in which the line bundle is the determinant bundle (top exterior power) of the tangent bundle. The Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
corresponds to a double cover of the circle (the θ → 2θ mapping) and can be viewed if we wish as having fibre two points, the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
or the real line: the data are equivalent.
In the case of the complex line bundle, we are looking in fact also for circle bundles. There are some celebrated ones, for example the Hopf fibrations of sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s to spheres.
The tautological bundle on projective space
The most important line bundle is the tautological line bundle on projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. The projectivization P(V) of a vector space V over a field k is defined to be the quotient of
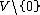by the action of the multiplicative group k×. Each point of P(V) therefore corresponds to a copy of k×, and these copies of k× can be assembled into a k×-bundle over P(V). k× differs from k only by a single point, and by adjoining that point to each fiber, we get a line bundle on P(V). This line bundle is called the tautological line bundle. This line bundle is sometimes denoted 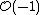since it corresponds to the dual of the Serre twisting sheaf 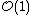.Maps to projective space
Suppose that X is a space and that L is a line bundle on X. A global section of L is a function s : X → L such that if p : L → X is the natural projection, then ps = idX. In a small neighborhood U in X in which L is trivial, the total space of the line bundle is the product of U and the underlying field k, and the section s restricts to a function U → k. However, the values of s depend on the choice of trivialization, and so they are determined only up to multiplication by a nowhere-vanishing function.Global sections determine maps to projective spaces in the following way: Choosing r + 1 not all zero points in a fiber of L chooses a fiber of the tautological line bundle on Pr, so choosing r + 1 non-simultaneously vanishing global sections of L determines a map from X into projective space Pr. This map sends the fibers of L to the fibers of the dual of the tautological bundle. More specifically, suppose that s0, ..., sr are global sections of L. In a small neighborhood U in X, these sections determine k-valued functions on U whose values depend on the choice of trivialization. However, they are determined up to simultaneous multiplication by a non-zero function, so their ratios are well-defined. That is, over a point x, the values s0(x), ..., sr(x) are not well-defined because a change in trivialization will multiply them each by a non-zero constant λ. But it will multiply them by the same constant λ, so the homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
[s0(x) : ... : sr(x)] are well-defined as long as the sections s0, ..., sr do not simultaneously vanish at x. Therefore, if the sections never simultaneously vanish, they determine a form [s0 : ... : sr] which gives a map from X to Pr, and the pullback of the dual of the tautological bundle under this map is L. In this way, projective space acquires a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
.
The universal way to determine a map to projective space is to map to the projectivization of the vector space of all sections of L. In the topological case, there is a non-vanishing section at every point which can be constructed using a bump function which vanishes outside a small neighborhood of the point. Because of this, the resulting map is defined everywhere. However, the codomain is usually far, far too big to be useful. The opposite is true in the algebraic and holomorphic settings. Here the space of global sections is often finite dimensional, but there may not be any non-vanishing global sections at a given point. In fact, it is possible for a bundle to have no non-zero global sections at all; this is the case for the tautological line bundle.
Determinant bundles
In general if V is a vector bundle on a space X, with constant fibre dimension n, the n-th exterior power of V taken fibre-by-fibre is a line bundle, called the determinant line bundle. This construction is in particular applied to the cotangent bundleCotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of a smooth manifold. The resulting determinant bundle is responsible for the phenomenon of tensor densities
Tensor density
In differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
, in the sense that for an orientable manifold it has a global section, and its tensor powers with any real exponent may be defined and used to 'twist' any vector bundle by tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
.
Characteristic classes, universal bundles and classifying spaces
The first Stiefel–Whitney classStiefel–Whitney class
In mathematics, in particular in algebraic topology and differential geometry, the Stiefel–Whitney class is an example of a \mathbb Z_2characteristic class associated to real vector bundles.-General presentation:...
classifies smooth real line bundles; in particular, the collection of (equivalence classes of) real line bundles are in correspondence with elements of the first cohomology with Z/2Z coefficients; this correspondence is in fact an isomorphism of abelian groups (the group operations being tensor product of line bundles and the usual addition on cohomology). Analogously, the first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
classifies smooth complex line bundles on a space, and the group of line bundles is isomorphic to the second cohomology class with integer coefficients. However, bundles can have equivalent smooth structure
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
s (and thus the same first Chern class) but different holomorphic structures. The Chern class statements are easily proven using the exponential sequence of sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on the manifold.
One can more generally view the classification problem from a homotopy-theoretic point of view. There is a universal bundle for real line bundles, and a universal bundle for complex line bundles. According to general theory about classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
s, the heuristic is to look for contractible spaces on which there are group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s of the respective groups C2 and S1, that are free actions. Those spaces can serve as the universal principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s, and the quotients for the actions as the classifying spaces BG. In these cases we can find those explicitly, in the infinite-dimensional analogues of real and complex projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
.
Therefore the classifying space BC2 is of the homotopy type of RP∞, the real projective space given by an infinite sequence of homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
. It carries the universal real line bundle; in terms of homotopy theory that means that any real line bundle L on a CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
X determines a classifying map from X to RP∞, making L a bundle isomorphic to the pullback of the universal bundle. This classifying map can be used to define the Stiefel-Whitney class of L, in the first cohomology of X with Z/2Z coefficients, from a standard class on RP∞.
In an analogous way, the complex projective space CP carries a universal complex line bundle. In this case classifying maps give rise to the first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of X, in H2(X) (integral cohomology).
There is a further, analogous theory with quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
ic (real dimension four) line bundles. This gives rise to one of the Pontryagin class
Pontryagin class
In mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
es, in real four-dimensional cohomology.
In this way foundational cases for the theory of characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es depend only on line bundles. According to a general splitting principle
Splitting principle
In mathematics, the splitting principle is a technique used to reduce questions about vector bundles to the case of line bundles.In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct...
this can determine the rest of the theory (if not explicitly).
There are theories of holomorphic line bundles on complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s, and invertible sheaves
Invertible sheaf
In mathematics, an invertible sheaf is a coherent sheaf S on a ringed space X, for which there is an inverse T with respect to tensor product of OX-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle...
in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, that work out a line bundle theory in those areas.