Circle bundle
Encyclopedia
In mathematics
, an (oriented
) circle bundle is an oriented fiber bundle
where the fiber is the circle
, or, more precisely, a principal U(1)-bundle
. It is homotopically equivalent to a complex line bundle
. In physics
, circle bundles are the natural geometric setting for electromagnetism
. A circle bundle is a special case of a sphere bundle.
s are an important example of 3-manifold
s. A more general class of 3-manifolds is Seifert fiber space
s, which may be viewed as a kind of "singular" circle bundle, or as a circle bundle over a two-dimensional orbifold
.
represented by a 2-form F, with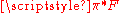
being cohomologous to zero. In particular, there always exists a 1-form A such that
Given a circle bundle P over M and its projection
one has the homomorphism
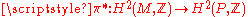
where
is the pullback
. Each homomorphism corresponds to a Dirac monopole; the integer cohomology groups correspond to the quantization of the electric charge
.
es of circle bundles over a manifold M are in one-to-one correspondence with the elements of the second integral cohomology group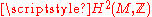
of M. This isomorphism is realized by the Euler class
.
Equivalently, the isomorphism classes correspond to homotopy classes of maps to the infinite-dimensional complex projective space
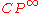, which is the classifying space of U(1). See classifying space for U(n)
.
In homotopy theory terms, the circle and the complex plane without its origin are equivalent. Circle bundles are, by the associated bundle
construction, equivalent to smooth complex line bundle
s because the transition functions of both can be made to live in C*. In this situation, the Euler class of the circle bundle or real two-plane bundle is the same as the first Chern class
of the line bundle.
See also: Wang sequence.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an (oriented
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
) circle bundle is an oriented fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
where the fiber is the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, or, more precisely, a principal U(1)-bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
. It is homotopically equivalent to a complex line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
. In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, circle bundles are the natural geometric setting for electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
. A circle bundle is a special case of a sphere bundle.
As 3-manifolds
Circle bundles over surfaceSurface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s are an important example of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s. A more general class of 3-manifolds is Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s, which may be viewed as a kind of "singular" circle bundle, or as a circle bundle over a two-dimensional orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
.
Relationship to electrodynamics
The Maxwell equations correspond to an electromagnetic fieldElectromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
represented by a 2-form F, with
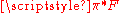being cohomologous to zero. In particular, there always exists a 1-form A such thatGiven a circle bundle P over M and its projection
one has the homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
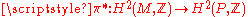
where
is the pullbackPullback
Suppose that φ:M→ N is a smooth map between smooth manifolds M and N; then there is an associated linear map from the space of 1-forms on N to the space of 1-forms on M. This linear map is known as the pullback , and is frequently denoted by φ*...
. Each homomorphism corresponds to a Dirac monopole; the integer cohomology groups correspond to the quantization of the electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
.
Classification
The isomorphism classIsomorphism class
An isomorphism class is a collection of mathematical objects isomorphic to each other.Isomorphism classes are often defined if the exact identity of the elements of the set is considered irrelevant, and the properties of the structure of the mathematical object are studied. Examples of this are...
es of circle bundles over a manifold M are in one-to-one correspondence with the elements of the second integral cohomology group
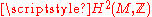of M. This isomorphism is realized by the Euler classEuler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
.
Equivalently, the isomorphism classes correspond to homotopy classes of maps to the infinite-dimensional complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, which is the classifying space of U(1). See classifying space for U(n)Classifying space for U(n)
In mathematics, the classifying space for the unitary group U is a space B together with a universal bundle E such that any hermitian bundle on a paracompact space X is the pull-back of E by a map X → B unique up to homotopy.This space with its universal fibration may be constructed as either# the...
.
In homotopy theory terms, the circle and the complex plane without its origin are equivalent. Circle bundles are, by the associated bundle
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
construction, equivalent to smooth complex line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s because the transition functions of both can be made to live in C*. In this situation, the Euler class of the circle bundle or real two-plane bundle is the same as the first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the line bundle.
See also: Wang sequence.