
Euler class
Encyclopedia
In mathematics
, specifically in algebraic topology
, the Euler class, named after Leonhard Euler
, is a characteristic class
of oriented, real vector bundle
s. Like other characteristic classes, it measures how "twisted" the vector bundle is. In the case of the tangent bundle
of a smooth manifold
, it generalizes the classical notion of Euler characteristic
.
Throughout this article is an oriented, real vector bundle of rank
is an oriented, real vector bundle of rank  .
.
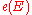 is an element of the integral cohomology
is an element of the integral cohomology
group
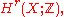
constructed as follows. An orientation
of amounts to a continuous choice of generator of the cohomology
amounts to a continuous choice of generator of the cohomology

of each fiber relative to the complement
relative to the complement 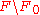 of its zero element
of its zero element 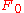 . From Thom isomorphism, this induces an orientation class
. From Thom isomorphism, this induces an orientation class
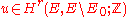
in the cohomology of relative to the complement
relative to the complement 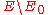 of the zero section
of the zero section 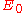 . The inclusions
. The inclusions
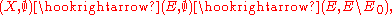
where includes into
includes into  as the zero section, induce maps
as the zero section, induce maps
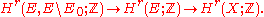
The Euler class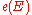 is the image of
is the image of  under the composition of these maps.
under the composition of these maps.
Functoriality: If is another oriented, real vector bundle and
is another oriented, real vector bundle and 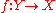 is continuous and covered by an orientation-preserving map
is continuous and covered by an orientation-preserving map  , then
, then 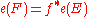 . In particular,
. In particular, 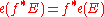 .
.
Whitney
sum formula: If is another oriented, real vector bundle, then the Euler class of the direct sum
is another oriented, real vector bundle, then the Euler class of the direct sum  is given by
is given by
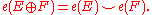
Its distinguishing feature is that it detects the existence of a non-vanishing section:
Normalization: If possesses a nowhere-zero section, then
possesses a nowhere-zero section, then 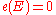 .
.
It also satisfies:
Orientation: If is
is  with the opposite orientation, then
with the opposite orientation, then 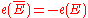 .
.
Note that unlike other characteristic classes, it is concentrated in a single dimension, which depends on the rank of the bundle: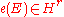 — there are no
— there are no 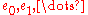 . In particular,
. In particular, 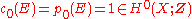 and
and  , but there is no
, but there is no 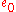 . This reflects the fact that the Euler class is unstable, as discussed below.
. This reflects the fact that the Euler class is unstable, as discussed below.
 a smooth, closed, oriented manifold), the Euler class corresponds to the vanishing of a section of
a smooth, closed, oriented manifold), the Euler class corresponds to the vanishing of a section of  in the following way. Let
in the following way. Let
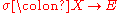
be a generic
smooth section and its zero locus. Then
its zero locus. Then  represents a homology
represents a homology
class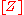 of codimension
of codimension
 in
in  , and
, and 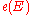 is the Poincaré dual of
is the Poincaré dual of 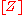 .
.
 is a compact submanifold, then the Euler class of the normal bundle
is a compact submanifold, then the Euler class of the normal bundle
of in
in  is naturally identified with the self-intersection of
is naturally identified with the self-intersection of  in
in  .
.
 in question is the tangent bundle of a compact, oriented,
in question is the tangent bundle of a compact, oriented,  -dimensional manifold, the Euler class is an element of the top cohomology of the manifold, which is naturally identified with the integers by evaluating cohomology classes on the fundamental homology class. Under this identification, the Euler class of the tangent bundle equals the Euler characteristic of the manifold. In the language of characteristic numbers, the Euler characteristic is the characteristic number corresponding to the Euler class.
-dimensional manifold, the Euler class is an element of the top cohomology of the manifold, which is naturally identified with the integers by evaluating cohomology classes on the fundamental homology class. Under this identification, the Euler class of the tangent bundle equals the Euler characteristic of the manifold. In the language of characteristic numbers, the Euler characteristic is the characteristic number corresponding to the Euler class.
Thus the Euler class is a generalization of the Euler characteristic to vector bundles other than tangent bundles. In turn, the Euler class is the archetype for other characteristic classes of vector bundles, in that each "top" characteristic class equals the Euler class, as follows.
Modding out by induces a map
induces a map
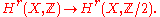
The image of the Euler class under this map is the top Stiefel-Whitney class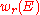 . One can view this Stiefel-Whitney class as "the Euler class, ignoring orientation".
. One can view this Stiefel-Whitney class as "the Euler class, ignoring orientation".
Any complex vector bundle of complex rank
of complex rank 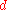 can be regarded as an oriented, real vector bundle
can be regarded as an oriented, real vector bundle  of real rank
of real rank  . The top Chern class
. The top Chern class
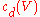 of the complex bundle equals the Euler class
of the complex bundle equals the Euler class 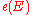 of the real bundle.
of the real bundle.
The Whitney sum is isomorphic to the complexification
is isomorphic to the complexification  , which is a complex bundle of rank
, which is a complex bundle of rank  . Comparing Euler classes, we see that
. Comparing Euler classes, we see that
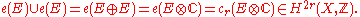
 is even, then this cohomology class
is even, then this cohomology class 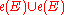 equals the top Pontryagin class
equals the top Pontryagin class
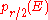 .
.
Under the splitting principle
, this corresponds to the square of the Vandermonde polynomial equaling the discriminant
: the Euler class corresponds to the Vandermonde polynomial, the basic alternating polynomial
, while the top Pontryagin class corresponds to the discriminant, a symmetric polynomial
.
More formally, the Euler class of a direct sum of line bundles is the Vandermonde polynomial (orientation determines the order of the line bundles up to sign), while top Pontryagin class is the discriminant.
. Concretely, this means that if 1 is a trivial bundle, then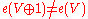 ; stable would mean that these are equal. In fact, adding a trivial bundle gives an obvious section, namely a constant on the trivial component, and 0 on the other, thus
; stable would mean that these are equal. In fact, adding a trivial bundle gives an obvious section, namely a constant on the trivial component, and 0 on the other, thus 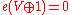 .
.
More abstractly, the cohomology class in the classifying space
 that represents the Euler class of a k-dimensional bundle is an unstable class: it is not the pull-back of a class in
that represents the Euler class of a k-dimensional bundle is an unstable class: it is not the pull-back of a class in 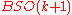 under the inclusion
under the inclusion 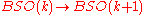 . Intuitively, it is not "consistently defined independently of dimension".
. Intuitively, it is not "consistently defined independently of dimension".
This can be seen intuitively in that the Euler class is a class whose degree depends on the dimension of the bundle (or manifold, if the tangent bundle): it is always of top dimension, while the other classes have a fixed dimension (the first Stiefel-Whitney class is in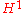 , etc.).
, etc.).
The fact that the Euler class is unstable should not be seen as a "defect": rather, from the point of view of stable homotopy, it means that the Euler class "detects unstable phenomena". For instance, the tangent bundle of spheres is stably trivial but not trivial (the usual inclusion of the sphere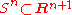 has trivial normal bundle, thus the tangent bundle of the sphere plus a trivial line bundle is the tangent bundle of Euclidean space, rectricted to
has trivial normal bundle, thus the tangent bundle of the sphere plus a trivial line bundle is the tangent bundle of Euclidean space, rectricted to 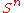 , which is trivial), thus other characteristic classes all vanish for the sphere, but the Euler class does not vanish for even spheres, providing a non-trivial invariant.
, which is trivial), thus other characteristic classes all vanish for the sphere, but the Euler class does not vanish for even spheres, providing a non-trivial invariant.
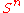 is:
is: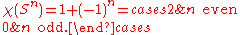
Thus, there is no non-vanishing section of the tangent bundle of even spheres, so the tangent bundle is not trivial, and they do not admit a Lie group structure.
For odd spheres,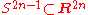 , a nowhere vanishing section is given by
, a nowhere vanishing section is given by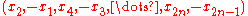
which shows that the Euler class vanishes; this is just n copies of the usual section over the circle.
As the Euler class for an even sphere corresponds to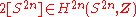 , we can use the fact that the Euler class of a Whitney sum of two bundles is just the cup product of the Euler class of the two bundles to see that there are no non-trivial subbundles of the tangent bundle of an even sphere.
, we can use the fact that the Euler class of a Whitney sum of two bundles is just the cup product of the Euler class of the two bundles to see that there are no non-trivial subbundles of the tangent bundle of an even sphere.
Since the tangent bundle of the sphere is stably trivial but not trivial, all other characteristic classes vanish on it, and the Euler class is the only ordinary cohomology class that detects non-triviality of the tangent bundle of spheres: to prove further results, one must use secondary cohomology operations or K-theory
.
 . It is a trivial line bundle, so it possesses a nowhere-zero section, and so its Euler class is
. It is a trivial line bundle, so it possesses a nowhere-zero section, and so its Euler class is  . It is also isomorphic to the tangent bundle of the circle; the fact that its Euler class is
. It is also isomorphic to the tangent bundle of the circle; the fact that its Euler class is  corresponds to the fact that the Euler characteristic of the circle is
corresponds to the fact that the Euler characteristic of the circle is  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the Euler class, named after Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, is a characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
of oriented, real vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s. Like other characteristic classes, it measures how "twisted" the vector bundle is. In the case of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a smooth manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, it generalizes the classical notion of Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
.
Throughout this article
 is an oriented, real vector bundle of rank
is an oriented, real vector bundle of rank  .
.Formal definition
The Euler class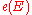 is an element of the integral cohomology
is an element of the integral cohomologyCohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
group
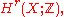
constructed as follows. An orientation
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
of
 amounts to a continuous choice of generator of the cohomology
amounts to a continuous choice of generator of the cohomology
of each fiber
 relative to the complement
relative to the complement 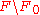 of its zero element
of its zero element 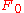 . From Thom isomorphism, this induces an orientation class
. From Thom isomorphism, this induces an orientation class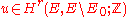
in the cohomology of
 relative to the complement
relative to the complement 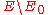 of the zero section
of the zero section 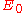 . The inclusions
. The inclusions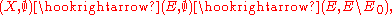
where
 includes into
includes into  as the zero section, induce maps
as the zero section, induce maps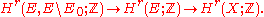
The Euler class
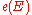 is the image of
is the image of  under the composition of these maps.
under the composition of these maps.Properties
The Euler class satisfies these properties, which are axioms of a characteristic class:Functoriality: If
 is another oriented, real vector bundle and
is another oriented, real vector bundle and 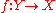 is continuous and covered by an orientation-preserving map
is continuous and covered by an orientation-preserving map  , then
, then 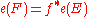 . In particular,
. In particular, 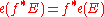 .
.Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
sum formula: If
 is another oriented, real vector bundle, then the Euler class of the direct sum
is another oriented, real vector bundle, then the Euler class of the direct sum  is given by
is given by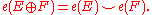
Its distinguishing feature is that it detects the existence of a non-vanishing section:
Normalization: If
 possesses a nowhere-zero section, then
possesses a nowhere-zero section, then 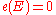 .
.It also satisfies:
Orientation: If
 is
is  with the opposite orientation, then
with the opposite orientation, then 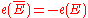 .
.Note that unlike other characteristic classes, it is concentrated in a single dimension, which depends on the rank of the bundle:
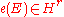 — there are no
— there are no 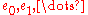 . In particular,
. In particular, 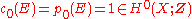 and
and  , but there is no
, but there is no 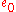 . This reflects the fact that the Euler class is unstable, as discussed below.
. This reflects the fact that the Euler class is unstable, as discussed below.Vanishing of section
Under mild conditions (such as a smooth, closed, oriented manifold), the Euler class corresponds to the vanishing of a section of
a smooth, closed, oriented manifold), the Euler class corresponds to the vanishing of a section of  in the following way. Let
in the following way. Let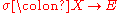
be a generic
Generic property
In mathematics, properties that hold for "typical" examples are called generic properties. For instance, a generic property of a class of functions is one that is true of "almost all" of those functions, as in the statements, "A generic polynomial does not have a root at zero," or "A generic...
smooth section and
 its zero locus. Then
its zero locus. Then  represents a homology
represents a homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
class
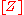 of codimension
of codimensionCodimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
 in
in  , and
, and 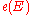 is the Poincaré dual of
is the Poincaré dual of 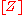 .
.Self-intersection
For example, if is a compact submanifold, then the Euler class of the normal bundle
is a compact submanifold, then the Euler class of the normal bundleNormal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
of
 in
in  is naturally identified with the self-intersection of
is naturally identified with the self-intersection of  in
in  .
.Relations to other invariants
In the special case when the bundle in question is the tangent bundle of a compact, oriented,
in question is the tangent bundle of a compact, oriented,  -dimensional manifold, the Euler class is an element of the top cohomology of the manifold, which is naturally identified with the integers by evaluating cohomology classes on the fundamental homology class. Under this identification, the Euler class of the tangent bundle equals the Euler characteristic of the manifold. In the language of characteristic numbers, the Euler characteristic is the characteristic number corresponding to the Euler class.
-dimensional manifold, the Euler class is an element of the top cohomology of the manifold, which is naturally identified with the integers by evaluating cohomology classes on the fundamental homology class. Under this identification, the Euler class of the tangent bundle equals the Euler characteristic of the manifold. In the language of characteristic numbers, the Euler characteristic is the characteristic number corresponding to the Euler class.Thus the Euler class is a generalization of the Euler characteristic to vector bundles other than tangent bundles. In turn, the Euler class is the archetype for other characteristic classes of vector bundles, in that each "top" characteristic class equals the Euler class, as follows.
Modding out by
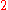 induces a map
induces a map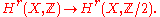
The image of the Euler class under this map is the top Stiefel-Whitney class
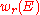 . One can view this Stiefel-Whitney class as "the Euler class, ignoring orientation".
. One can view this Stiefel-Whitney class as "the Euler class, ignoring orientation".Any complex vector bundle
 of complex rank
of complex rank 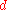 can be regarded as an oriented, real vector bundle
can be regarded as an oriented, real vector bundle  of real rank
of real rank  . The top Chern class
. The top Chern classChern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
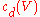 of the complex bundle equals the Euler class
of the complex bundle equals the Euler class 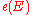 of the real bundle.
of the real bundle.The Whitney sum
 is isomorphic to the complexification
is isomorphic to the complexification  , which is a complex bundle of rank
, which is a complex bundle of rank  . Comparing Euler classes, we see that
. Comparing Euler classes, we see that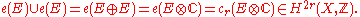
Squares to top Pontryagin class
If the rank is even, then this cohomology class
is even, then this cohomology class 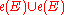 equals the top Pontryagin class
equals the top Pontryagin classPontryagin class
In mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
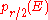 .
.Under the splitting principle
Splitting principle
In mathematics, the splitting principle is a technique used to reduce questions about vector bundles to the case of line bundles.In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct...
, this corresponds to the square of the Vandermonde polynomial equaling the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
: the Euler class corresponds to the Vandermonde polynomial, the basic alternating polynomial
Alternating polynomial
In algebra, an alternating polynomial is a polynomial f such that if one switches any two of the variables, the polynomial changes sign:f = -f....
, while the top Pontryagin class corresponds to the discriminant, a symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
.
More formally, the Euler class of a direct sum of line bundles is the Vandermonde polynomial (orientation determines the order of the line bundles up to sign), while top Pontryagin class is the discriminant.
Unstable
Unlike the other characteristic classes, the Euler class is unstable, in the sense of stable homotopy theoryStable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
. Concretely, this means that if 1 is a trivial bundle, then
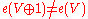 ; stable would mean that these are equal. In fact, adding a trivial bundle gives an obvious section, namely a constant on the trivial component, and 0 on the other, thus
; stable would mean that these are equal. In fact, adding a trivial bundle gives an obvious section, namely a constant on the trivial component, and 0 on the other, thus 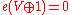 .
.More abstractly, the cohomology class in the classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
 that represents the Euler class of a k-dimensional bundle is an unstable class: it is not the pull-back of a class in
that represents the Euler class of a k-dimensional bundle is an unstable class: it is not the pull-back of a class in 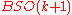 under the inclusion
under the inclusion 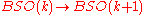 . Intuitively, it is not "consistently defined independently of dimension".
. Intuitively, it is not "consistently defined independently of dimension".This can be seen intuitively in that the Euler class is a class whose degree depends on the dimension of the bundle (or manifold, if the tangent bundle): it is always of top dimension, while the other classes have a fixed dimension (the first Stiefel-Whitney class is in
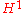 , etc.).
, etc.).The fact that the Euler class is unstable should not be seen as a "defect": rather, from the point of view of stable homotopy, it means that the Euler class "detects unstable phenomena". For instance, the tangent bundle of spheres is stably trivial but not trivial (the usual inclusion of the sphere
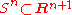 has trivial normal bundle, thus the tangent bundle of the sphere plus a trivial line bundle is the tangent bundle of Euclidean space, rectricted to
has trivial normal bundle, thus the tangent bundle of the sphere plus a trivial line bundle is the tangent bundle of Euclidean space, rectricted to 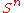 , which is trivial), thus other characteristic classes all vanish for the sphere, but the Euler class does not vanish for even spheres, providing a non-trivial invariant.
, which is trivial), thus other characteristic classes all vanish for the sphere, but the Euler class does not vanish for even spheres, providing a non-trivial invariant.Spheres
The Euler characteristic of the n-sphere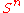 is:
is: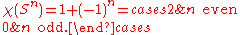
Thus, there is no non-vanishing section of the tangent bundle of even spheres, so the tangent bundle is not trivial, and they do not admit a Lie group structure.
For odd spheres,
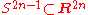 , a nowhere vanishing section is given by
, a nowhere vanishing section is given by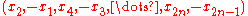
which shows that the Euler class vanishes; this is just n copies of the usual section over the circle.
As the Euler class for an even sphere corresponds to
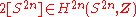 , we can use the fact that the Euler class of a Whitney sum of two bundles is just the cup product of the Euler class of the two bundles to see that there are no non-trivial subbundles of the tangent bundle of an even sphere.
, we can use the fact that the Euler class of a Whitney sum of two bundles is just the cup product of the Euler class of the two bundles to see that there are no non-trivial subbundles of the tangent bundle of an even sphere.Since the tangent bundle of the sphere is stably trivial but not trivial, all other characteristic classes vanish on it, and the Euler class is the only ordinary cohomology class that detects non-triviality of the tangent bundle of spheres: to prove further results, one must use secondary cohomology operations or K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
.
Circle
The cylinder is a line bundle over the circle, by the natural projection . It is a trivial line bundle, so it possesses a nowhere-zero section, and so its Euler class is
. It is a trivial line bundle, so it possesses a nowhere-zero section, and so its Euler class is  . It is also isomorphic to the tangent bundle of the circle; the fact that its Euler class is
. It is also isomorphic to the tangent bundle of the circle; the fact that its Euler class is  corresponds to the fact that the Euler characteristic of the circle is
corresponds to the fact that the Euler characteristic of the circle is  .
.

