In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a vector bundle is a topological

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

 construction that makes precise the idea of a family of vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

s parameterized by another space X (for example X could be a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

, a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

, or an algebraic variety

Algebraic variety

In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...

): to every point x of the space X we associate (or "attach") a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over X.

The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space V such that V(x) = V for all x in X: in this case there is a copy of V for each x in X and these copies fit together to form the vector bundle X × V over X. Such vector bundles are said to be trivial. A more complicated (and prototypical) class of examples are the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

s of smooth (or differentiable) manifolds

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

: to every point of such a manifold we attach the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

 to the manifold at that point. Tangent bundles are not, in general, trivial bundles: for example, the tangent bundle of the (two dimensional) sphere is non-trivial by the hairy ball theorem

Hairy ball theorem

The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...

. In general, a manifold is said to be parallelizable if and only if its tangent bundle is trivial.

Vector bundles are almost always required to be locally trivial, however, which means they are examples of fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

s. Also, the vector spaces are usually required to be over the real or complex numbers, in which case the vector bundle is said to be a real or complex vector bundle (respectively). Complex vector bundles can be viewed as real vector bundles with additional structure. In the following, we focus on real vector bundles in the category of topological spaces

Category of topological spaces

In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...

.

Definition and first consequences

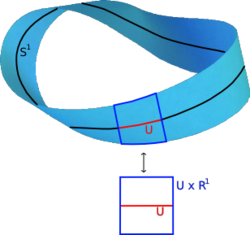
A real vector bundle consists of:

1. topological spaces X (base space) and E (total space)
2. a continuous
   Continuous function
   In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
   
    surjection π : E → X (bundle projection)
3. for every x in X, the structure of a finite-dimensional real
   Real number
   In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
   
    vector space
   Vector space
   A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
   
    on the fiber
   Fiber bundle
   In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
   
    π⁻¹({x})

where the following compatibility condition is satisfied: for every point in X, there is an open neighborhood U, a natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

 k, and a homeomorphism

Homeomorphism

In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...

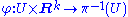
such that for all x ∈ U,

• (π∘φ)(x,v) = x for all vectors v in R^k, and

• the map v φ(x,v) is an isomorphism between the vector spaces R^k and π⁻¹({x}).

The open neighborhood U together with the homeomorphism φ is called a local trivialization of the vector bundle. The local trivialization shows that locally the map π "looks like" the projection of U × R^k on U.

Every fiber π⁻¹({x}) is a finite-dimensional real vector space and hence has a dimension k_x. The local trivializations show that the function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 x k_x is locally constant, and is therefore constant on each connected component

Locally connected space

In topology and other branches of mathematics, a topological space X islocally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.-Background:...

 of X. If k_x is equal to a constant k on all of X, then k is called the rank of the vector bundle, and E is said to be a vector bundle of rank k. Often the definition of a vector bundle includes that the rank is well defined, so that k_x is constant. Vector bundles of rank 1 are called line bundle

Line bundle

In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...

s, while those of rank 2 are less commonly called plane bundles.

The Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

 X × R^k , equipped with the projection X × R^k → X, is called the trivial bundle of rank k over X.

Transition functions

Given a vector bundle E → X of rank k, and a pair of neighborhoods U and V over which the bundle trivializes via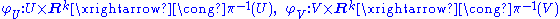
the composite function
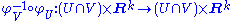
is well-defined on the overlap, and satisfies
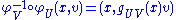
for some GL(k)-valued function
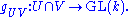
These are called the transition functions (or the coordinate transformations) of the vector bundle.

The set of transition functions forms a Čech cocycle in the sense that
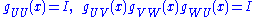
for all U,V,W over which the bundle trivializes. Thus the data (E,X,π,R^k) defines a fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

; the additional data of the g_UV specifies a GL(k) structure group in which the action on the fiber is the standard action of GL(k).

Conversely, given a fiber bundle (E,X,π,R^k) with a GL(k) cocycle acting in the standard way on the fiber R^k, there is associated a vector bundle. This is sometimes taken as the definition of a vector bundle.

Vector bundle morphisms

A morphism

Morphism

In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...

 from the vector bundle π₁ : E₁ → X₁ to the vector bundle π₂ : E₂ → X₂ is given by a pair of continuous maps f : E₁ → E₂ and g : X₁ → X₂ such that

• g ∘ π₁ = π₂ ∘ f

• for every x in X₁, the map π₁⁻¹({x}) → π₂⁻¹({g(x)}) induced by f is a linear map between vector spaces.

Note that g is determined by f (because π₁ is surjective), and f is then said to cover g.

The class of all vector bundles together with bundle morphisms forms a category

Category (mathematics)

In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...

. Restricting to vector bundles for which the spaces are manifolds (and the bundle projections are smooth maps) and smooth bundle morphisms we obtain the category of smooth vector bundles. Vector bundle morphisms are a special case of the notion of a bundle map

Bundle map

In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...

 between fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

s, and are also often called (vector) bundle homomorphisms.

A bundle homomorphism from E₁ to E₂ with an inverse which is also a bundle homomorphism (from E₂ to E₁) is called a (vector) bundle isomorphism, and then E₁ and E₂ are said to be isomorphic vector bundles. An isomorphism of a (rank k) vector bundle E over X with the trivial bundle (of rank k over X) is called a trivialization of E, and E is then said to be trivial (or trivializable). The definition of a vector bundle shows that any vector bundle is locally trivial.

We can also consider the category of all vector bundles over a fixed base space X. As morphisms in this category we take those morphisms of vector bundles whose map on the base space is the identity map

Identity function

In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...

 on X. That is, bundle morphisms for which the following diagram commutes

Commutative diagram

In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...

:
(Note that this category is not abelian

Abelian category

In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...

; the kernel

Kernel (mathematics)

In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...

 of a morphism of vector bundles is in general not a vector bundle in any natural way.)

A vector bundle morphism between vector bundles π₁ : E₁ → X₁ and π₂ : E₂ → X₂ covering a map g from X₁ to X₂ can also be viewed as a vector bundle morphism over X₁ from E₁ to the pullback bundle

Pullback bundle

In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...

 g*E₂.

Sections and locally free sheaves

Given a vector bundle π : E → X and an open subset U of X, we can consider sections of π on U, i.e. continuous functions s : U → E where the composite π∘s is such that for all u in U. Essentially, a section assigns to every point of U a vector from the attached vector space, in a continuous manner.
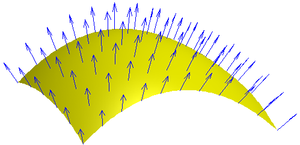
As an example, sections of the tangent bundle of a differential manifold are nothing but vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

s on that manifold.

Let F(U) be the set of all sections on U. F(U) always contains at least one element, namely the zero section: the function s that maps every element x of U to the zero element of the vector space π⁻¹({x}). With the pointwise addition and scalar multiplication of sections, F(U) becomes itself a real vector space. The collection of these vector spaces is a sheaf

Sheaf (mathematics)

In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...

 of vector spaces on X.

If s is an element of F(U) and α : U → R is a continuous map, then αs (pointwise scalar multiplication) is in F(U). We see that F(U) is a module

Module (mathematics)

In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...

 over the ring of continuous real-valued functions on U. Furthermore, if O_X denotes the structure sheaf of continuous real-valued functions on X, then F becomes a sheaf of O_X-modules.

Not every sheaf of O_X-modules arises in this fashion from a vector bundle: only the locally free ones do. (The reason: locally we are looking for sections of a projection U × R^k → U; these are precisely the continuous functions U → R^k, and such a function is an k-tuple of continuous functions U → R.)

Even more: the category of real vector bundles on X is equivalent

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

 to the category of locally free and finitely generated sheaves of O_X-modules.
So we can think of the category of real vector bundles on X as sitting inside the category of sheaves of O_X-modules; this latter category is abelian, so this is where we can compute kernels and cokernels of morphisms of vector bundles.

Note that a rank n vector bundle is trivial if and only if it has n linearly independent global sections.

Operations on vector bundles

Most operations on vector spaces can be extended to vector bundles by performing the vector space operation fiberwise.

For example, if E is a vector bundle over X, then the there is a bundle E* over X, called the dual bundle

Dual bundle

In mathematics, the dual bundle of a vector bundle π : E → X is a vector bundle π* : E* → X whose fibers are the dual spaces to the fibers of E...

, whose fiber at x∈X is the dual vector space (E_x)*. Formally E* can be defined as the set of pairs (x,φ), where x∈X and φ∈(E_x)*. The dual bundle is locally trivial because the dual space

Transpose

In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...

 of the inverse of a local trivialization of E is a local trivialization of E*: the key point here is that the operation of taking the dual vector space is functorial.

There are many functorial operations which can be performed on pairs of vector spaces (over the same field), and these extend straightforwardly to pairs of vector bundles E, F on X (over the given field). A few examples follow.

• The Whitney sum (named for Hassler Whitney
  Hassler Whitney
  Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
  
  ) or direct sum bundle of E and F is a vector bundle over X whose fiber over x is the direct sum
  Direct sum of modules
  In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
  
    of the vector spaces E_x and F_x.

• The tensor product bundle  is defined in a similar way, using fiberwise tensor product
  Tensor product
  In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
  
   of vector spaces.

• The Hom-bundle Hom(E,F) is a vector bundle whose fiber at x is the space of linear maps from E_x to F_x (which is often denoted Hom(E_x,F_x) or L(E_x,F_x)). The Hom-bundle is so-called (and useful) because there is a bijection between vector bundle homomorphisms from E to F over X and sections of Hom(E,F) over X.

• The dual vector bundle
  Dual bundle
  In mathematics, the dual bundle of a vector bundle π : E → X is a vector bundle π* : E* → X whose fibers are the dual spaces to the fibers of E...
  
   E^∗ is the Hom bundle Hom(E,R×X) of bundle homomorphisms of E and the trivial bundle R×X. There is a canonical vector bundle isomorphism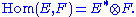

Each of these operations is a particular example of a general feature of bundles: that many operations that can be performed on the category of vector spaces can also be performed on the category of vector bundles in a functor

Functor

In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....

ial manner. This is made precise in the language of smooth functor

Smooth functor

In differential topology, a branch of mathematics, a smooth functor is a type of functor defined on finite-dimensional real vector spaces. Intuitively, a smooth functor is smooth in the sense that it sends smoothly parameterized families of vector spaces to smoothly parameterized families of...

s. An operation of a different nature is the pullback bundle

Pullback bundle

In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...

 construction. Given a vector bundle E → Y and a continuous map f : X → Y one can "pull back" E to a vector bundle f*E over X. The fiber over a point x ∈ X is essentially just the fiber over f(x) ∈ Y. Hence, Whitney summing can be defined as the pullback bundle of the diagonal map from X to X x X where the bundle over X x X is E x F.

Additional structures and generalizations

Vector bundles are often given more structure. For instance, vector bundles may be equipped with a vector bundle metric

Metric (vector bundle)

In differential geometry, the notion of a metric tensor can be extended to an arbitrary vector bundle. Specifically, if M is a topological manifold and E → M a vector bundle on M, then a metric on E is a bundle map g : E ×M E → M × R from the fiber product of E with itself...

. Usually this metric is required to be positive definite, in which case each fibre of E becomes a Euclidean space. A vector bundle with a complex structure corresponds to a complex vector bundle, which may also be obtained by replacing real vector spaces in the definition with complex ones and requiring that all mappings be complex-linear in the fibers. More generally, one can typically understand the additional structure imposed on a vector bundle in terms of the resulting reduction of the structure group of a bundle. Vector bundles over more general topological fields may also be used.

If instead of a finite-dimensional vector space, if the fiber F is taken to be a Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

 then a Banach bundle

Banach bundle

In mathematics, a Banach bundle is a vector bundle each of whose fibres is a Banach space, i.e. a complete normed vector space, possibly of infinite dimension.-Definition of a Banach bundle:...

 is obtained. Specifically, one must require that the local trivializions are Banach space isomorphisms (rather than just linear isomorphisms) on each of the fibers and that, furthermore, the transitions
are continuous mappings of Banach manifold

Banach manifold

In mathematics, a Banach manifold is a manifold modeled on Banach spaces. Thus it is a topological space in which each point has a neighbourhood homeomorphic to an open set in a Banach space...

s. In the corresponding theory for C^p bundles, all mappings are required to be C^p.

Vector bundles are special fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

s, those whose fibers are vector spaces and whose cocycle respects the vector space structure. More general fiber bundles can be constructed in which the fiber may have other structures; for example sphere bundles are fibered by spheres.

Smooth vector bundles

A vector bundle (E,p,M) is smooth, if E and M are smooth manifolds

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

, p : E → M is a smooth map, and the local trivializations are diffeomorphism

Diffeomorphism

In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...

s. Depending on the required degree of smoothness, there are different corresponding notions of C^p bundles, infinitely differentiable C^∞-bundles and real analytic C^ω-bundles. In this section we will concentrate on C^∞-bundles. The most important example of a C^∞-vector bundle is the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

 (TM,π_TM,M) of a C^∞-manifold M.

The C^∞-vector bundles (E,p,M) have a very important property not shared by more general C^∞-fibre bundles. Namely, the tangent space T_v(E_x) at any v∈E_x can be naturally identified with the fibre E_x itself. This identification is obtained through the vertical lift
vl_v:E_x→T_v(E_x), defined as
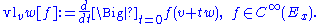
The vertical lift can also be seen as a natural C^∞-vector bundle isomorphism p*E→VE, where
(p*E,p*p,E) is the pull-back bundle of (E,p,M) over E through p:E→M, and
VE:=Ker(p_*)⊂TE
is the vertical tangent bundle, a natural vector subbundle of the tangent bundle (TE,π_TE,E) of the total space E.

The slit vector bundle E/0, obtained from (E,p,M) by removing the zero section 0⊂E, carries a natural vector field V_v := vl_vv, known as the canonical vector field.
More formally, V is a smooth section of (TE,π_TE,E), and it can also be defined as the infinitesimal generator of the Lie-group action

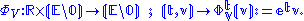
For any smooth vector bundle (E,p,M) the total space TE of its tangent bundle (TE,π_TE,E) has a natural secondary vector bundle structure

Secondary vector bundle structure

In mathematics, particularly differential topology, the secondary vector bundle structurerefers to the natural vector bundle structure on the total space TE of the tangent bundle of a smooth vector bundle , induced by the push-forward p*:TE→TM of the original projection map p:E→M.In the...

 (TE,p_*,TM), where p_* is the push-forward of the canonical projection p:E→M. The vector bundle operations in this secondary vector bundle structure are the push-forwards +_*:T(E×E)→TE and λ_*:TE→TE of the original addition +:E×E→E and scalar multiplication λ:E→E.

K-theory

The K-theory group

K(X)

of a manifold is defined as the abelian group generated by isomorphism classes [E] of (complex) vector bundles modulo the relation that whenever we have an exact sequence

Exact sequence

An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...

0 → A → B → C → 0

then

[B]=[A]+[C]

in topological K-theory

Topological K-theory

In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...

. KO-theory is a version of this construction which considers real vector bundles. K-theory with compact supports can also be defined, as well as higher K-theory groups.

The famous periodicity theorem of Raoul Bott

Raoul Bott

Raoul Bott, FRS was a Hungarian mathematician known for numerous basic contributions to geometry in its broad sense...

 asserts that the K-theory of any space X is isomorphic to that of the Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

X × S²,

where S² denotes the 2-sphere.

In algebraic geometry

Algebraic geometry

Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...

, one considers the K-theory groups consisting of coherent sheaves

Coherent sheaf

In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...

 on a scheme

Scheme (mathematics)

In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...

 X, as well as the K-theory groups of vector bundles on the scheme with the above equivalence relation. The two constructs are the same provided that the underlying scheme is smooth.

General notions

• Grassmannian
  Grassmannian
  In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
  
  : classifying spaces for vector bundle, among which Projective space
  Projective space
  In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
  
  s for line bundle
  Line bundle
  In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
  
  s
• Characteristic class
  Characteristic class
  In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
  
  
• Splitting principle
  Splitting principle
  In mathematics, the splitting principle is a technique used to reduce questions about vector bundles to the case of line bundles.In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct...
  
  

Topology and differential geometry

• Fiber bundle
  Fiber bundle
  In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
  
  : the general topological notion, among which Covering spaces
• Connection (vector bundle)
  Connection (vector bundle)
  In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
  
  : the notion needed to differentiate sections of vector bundles.
• Sheaf (mathematics)
  Sheaf (mathematics)
  In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
  
  
• Topological K-theory
  Topological K-theory
  In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
  
  

Algebraic and analytic geometry

• Coherent sheaf
  Coherent sheaf
  In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
  
  , in particular Picard group
• Holomorphic vector bundle
  Holomorphic vector bundle
  In mathematics, a holomorphic vector bundle is a complex vector bundle over a complex manifold X such that the total space E is a complex manifold and the projection map \pi:E\to X is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the...
  
  

External links

• Why is it useful to study vector bundles ? on MathOverflow
• Why is it useful to classify the vector bundles of a space ?