Bundle map
Encyclopedia
In mathematics
, a bundle map (or bundle morphism) is a morphism
in the category
of fiber bundle
s. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space
. There are also several variations on the basic theme, depending on precisely which category of fiber bundles is under consideration. In the first three sections, we will consider general fiber bundles in the category of topological spaces
. Then in the fourth section, some other examples will be given.
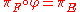. That is, the diagram
should commute
. Equivalently, for any point x in M, φ maps the fiber Ex = πE−1({x}) of E over x to the fiber Fx = πF−1({x}) of F over x.
commutes, that is,
. In other words, φ is fiber-preserving, and f is the induced map on the space of fibers of E: since πE is surjective, f is uniquely determined by φ. For a given f, such a bundle map φ is said to be a bundle map covering f.
Conversely, general bundle maps can be reduced to bundle maps over a fixed base space using the notion of a pullback bundle
. If πF:F→ N is a fiber bundle over N and f:M→ N is a continuous map, then the pullback of F by f is a fiber bundle f*F over M whose fiber over x is given by (f*F)x.= Ff(x). It then follows that a bundle map from E to F covering f is the same thing as a bundle map from E to f*F over M.
First, one can consider fiber bundles in a different category of spaces. This leads, for example, to the notion of a smooth bundle map between smooth fiber bundles over a smooth manifold.
Second, one can consider fiber bundles with extra structure in their fibers, and restrict attention to bundle maps which preserve this structure. This leads, for example, to the notion of a (vector) bundle homomorphism between vector bundle
s, in which the fibers are vector spaces, and a bundle map φ is required to be a linear map on each fiber. In this case, such a bundle map φ (covering f) may also be viewed as a section
of the vector bundle Hom(E,f*F) over M, whose fiber over x is the vector space Hom(Ex,Ff(x)) (also denoted L(Ex,Ff(x))) of linear maps from
Ex to Ff(x).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a bundle map (or bundle morphism) is a morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
. There are also several variations on the basic theme, depending on precisely which category of fiber bundles is under consideration. In the first three sections, we will consider general fiber bundles in the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
. Then in the fourth section, some other examples will be given.
Bundle maps over a common base
Let πE:E→ M and πF:F→ M be fiber bundles over a space M. Then a bundle map from E to F over M is a continuous map φ:E→ F such that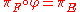. That is, the diagramshould commute
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
. Equivalently, for any point x in M, φ maps the fiber Ex = πE−1({x}) of E over x to the fiber Fx = πF−1({x}) of F over x.
General morphisms of fiber bundles
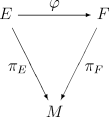
Let πE:E→ M and πF:F→ N be fiber bundles over spaces M and N respectively. Then a continuous map φ:E→ F is called a bundle map from E to F if there is a continuous map f:M→ N such that the diagramcommutes, that is,
. In other words, φ is fiber-preserving, and f is the induced map on the space of fibers of E: since πE is surjective, f is uniquely determined by φ. For a given f, such a bundle map φ is said to be a bundle map covering f.Relation between the two notions
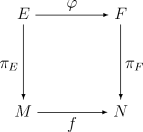
It follows immediately from the definitions that a bundle map over M (in the first sense) is the same thing as a bundle map covering the identity map of M.Conversely, general bundle maps can be reduced to bundle maps over a fixed base space using the notion of a pullback bundle
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
. If πF:F→ N is a fiber bundle over N and f:M→ N is a continuous map, then the pullback of F by f is a fiber bundle f*F over M whose fiber over x is given by (f*F)x.= Ff(x). It then follows that a bundle map from E to F covering f is the same thing as a bundle map from E to f*F over M.
Variants and generalizations
There are two kinds of variation of the general notion of a bundle map.First, one can consider fiber bundles in a different category of spaces. This leads, for example, to the notion of a smooth bundle map between smooth fiber bundles over a smooth manifold.
Second, one can consider fiber bundles with extra structure in their fibers, and restrict attention to bundle maps which preserve this structure. This leads, for example, to the notion of a (vector) bundle homomorphism between vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s, in which the fibers are vector spaces, and a bundle map φ is required to be a linear map on each fiber. In this case, such a bundle map φ (covering f) may also be viewed as a section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of the vector bundle Hom(E,f*F) over M, whose fiber over x is the vector space Hom(Ex,Ff(x)) (also denoted L(Ex,Ff(x))) of linear maps from
Ex to Ff(x).