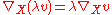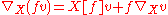Secondary vector bundle structure
Encyclopedia
In mathematics
, particularly differential topology
, the secondary vector bundle structure
refers to the natural vector bundle
structure (TE,p*,TM) on the total space TE of the tangent bundle
of a smooth vector bundle (E,p,M), induced by the push-forward p*:TE→TM of the original projection map p:E→M.
In the special case (E,p,M)=(TM,πTM,M), where TE=TTM is the double tangent bundle
, the secondary vector bundle (TTM,(πTM)*,TM) is isomorphic to the tangent bundle
(TTM,πTTM,TM) of TM through the canonical flip
.
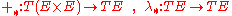
of the original addition and scalar multiplication
as its vector space operations. The triple (TE,p*,TM) becomes a smooth vector bundle with these vector space operations on its fibres.
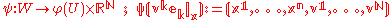
be a coordinate system on E adapted to it. Then
so the fiber of the secondary vector bundle structure at X∈TxM is of the form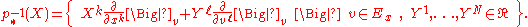
Now it turns out that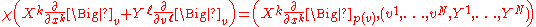
gives a local trivialization χ:TW→TU×R2N for (TE,p*,TM), and the push-forwards of the original vector space operations read in the adapted coordinates as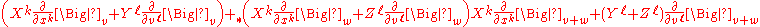
and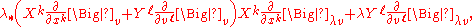
so each fibre (p*)-1(X)⊂TE is a vector space and the triple (TE,p*,TM) is a smooth vector bundle.

on a vector bundle (E,p,M) can be characterized in terms of the connector map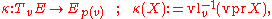
where vlv:E→VvE is the vertical lift
, and vprv:TvE→VvE is the vertical projection
. The mapping
induced by an Ehresmann connection is a covariant derivative
on Γ(E) in the sense that
if and only if the connector map is linear with respect to the secondary vector bundle structure (TE,p*,TM) on TE. Then the connection is called linear. Note that the connector map is automatically linear with respect to the tangent bundle structure (TE,πTE,E).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, the secondary vector bundle structure
refers to the natural vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
structure (TE,p*,TM) on the total space TE of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a smooth vector bundle (E,p,M), induced by the push-forward p*:TE→TM of the original projection map p:E→M.
In the special case (E,p,M)=(TM,πTM,M), where TE=TTM is the double tangent bundle
Double tangent bundle
In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle of the total space TM of the tangent bundle of a smooth manifold M...
, the secondary vector bundle (TTM,(πTM)*,TM) is isomorphic to the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
(TTM,πTTM,TM) of TM through the canonical flip
Double tangent bundle
In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle of the total space TM of the tangent bundle of a smooth manifold M...
.
Construction of the secondary vector bundle structure
Let (E,p,M) be a smooth vector bundle of rank N. Then the preimage (p*)-1(X)⊂TE of any tangent vector X∈TM in the push-forward p*:TE→TM of the canonical projection p:E→M is a smooth submanifold of dimension 2N, and it becomes a vector space with the push-forwards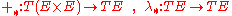
of the original addition and scalar multiplication

as its vector space operations. The triple (TE,p*,TM) becomes a smooth vector bundle with these vector space operations on its fibres.
Proof
Let (U,φ) be a local coordinate system on the base manifold M with φ(x)=(x1,...,xn) and let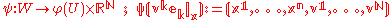
be a coordinate system on E adapted to it. Then

so the fiber of the secondary vector bundle structure at X∈TxM is of the form
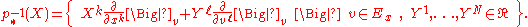
Now it turns out that
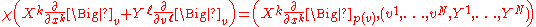
gives a local trivialization χ:TW→TU×R2N for (TE,p*,TM), and the push-forwards of the original vector space operations read in the adapted coordinates as
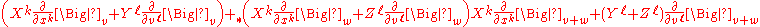
and
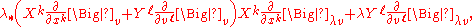
so each fibre (p*)-1(X)⊂TE is a vector space and the triple (TE,p*,TM) is a smooth vector bundle.
Linearity of connections on vector bundles
The general Ehresmann connectionEhresmann connection
In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...

on a vector bundle (E,p,M) can be characterized in terms of the connector map
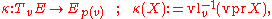
where vlv:E→VvE is the vertical lift
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, and vprv:TvE→VvE is the vertical projection
Ehresmann connection
In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...
. The mapping

induced by an Ehresmann connection is a covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
on Γ(E) in the sense that
if and only if the connector map is linear with respect to the secondary vector bundle structure (TE,p*,TM) on TE. Then the connection is called linear. Note that the connector map is automatically linear with respect to the tangent bundle structure (TE,πTE,E).
See also
- Connection (vector bundle)Connection (vector bundle)In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
- Double tangent bundleDouble tangent bundleIn mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle of the total space TM of the tangent bundle of a smooth manifold M...
- Ehresmann connectionEhresmann connectionIn differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...
- Vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...