Scheme (mathematics)
Encyclopedia
In mathematics
, a scheme is an important concept connecting the fields of algebraic geometry
, commutative algebra
and number theory
. Schemes were introduced by Alexander Grothendieck
so as to broaden the notion of algebraic variety
; some consider schemes to be the basic object of study of modern algebraic geometry. Technically, a scheme is a topological space
together with commutative ring
s for all of its open sets, which arises from gluing together spectra
(spaces of prime ideal
s) of commutative rings along their open subsets.
had often used the somewhat foggy concept of "generic point
" when proving statements about algebraic varieties. What is true for the generic point is true for all points of the variety except a small number of special points. In the 1920s, Emmy Noether
had first suggested a way to clarify the concept: start with the coordinate ring of the variety (the ring of all polynomial functions defined on the variety); the maximal ideal
s of this ring will correspond to ordinary points of the variety (under suitable conditions), and the non-maximal prime ideal
s will correspond to the various generic points, one for each subvariety. By taking all prime ideals, one thus gets the whole collection of ordinary and generic points. Noether did not pursue this approach.
In the 1930s, Wolfgang Krull
turned things around and took a radical step: start with any commutative ring, consider the set of its prime ideals, turn it into a topological space
by introducing the Zariski topology
, and study the algebraic geometry of these quite general objects. Others did not see the point of this generality and Krull abandoned it.
André Weil
was especially interested in algebraic geometry over finite field
s and other rings. In the 1940s he returned to the prime ideal approach; he needed an abstract variety (outside projective space
) for foundational reasons, particularly for the existence in an algebraic setting of the Jacobian variety
. In Weil's main foundational book (1946), generic points are constructed by taking points in a very large algebraically closed field, called a universal domain.
In 1944 Oscar Zariski
had defined an abstract Zariski–Riemann space
from the function field of an algebraic variety
, for the needs of birational geometry
: this is like a direct limit
of ordinary varieties (under 'blowing up'), and the construction, reminiscent of locale theory, used valuation ring
s as points.
In the 1950s, Jean-Pierre Serre
, Claude Chevalley
and Masayoshi Nagata
, motivated largely by the Weil conjectures
relating number theory
and algebraic geometry
, pursued similar approaches with prime ideals as points. According to Pierre Cartier
, the word scheme was first used in the 1956 Chevalley Seminar, in which Chevalley was pursuing Zariski's ideas; and it was André Martineau who suggested to Serre the move to the current spectrum of a ring
in general.
then gave the decisive definition, bringing to a conclusion a generation of experimental suggestions and partial developments. He defined the spectrum
of a commutative ring as the space of prime ideals with Zariski topology, but augments it with a sheaf
of rings: to every Zariski-open set he assigns a commutative ring, thought of as the ring of "polynomial functions" defined on that set. These objects are the "affine schemes"; a general scheme is then obtained by "gluing together" several such affine schemes, in analogy to the fact that general varieties can be obtained by gluing together affine varieties.
The generality of the scheme concept was initially criticized: some schemes are removed from having straightforward geometrical interpretation, which made the concept difficult to grasp. However, admitting arbitrary schemes makes the whole category of schemes better-behaved. Moreover, natural considerations regarding, for example, moduli space
s, lead to schemes which are "non-classical". The occurrence of these schemes that are not varieties (nor built up simply from varieties) in problems that could be posed in classical terms made for the gradual acceptance of the new foundations of the subject.
Subsequent work on algebraic space
s and algebraic stacks by Deligne
, Mumford
, and Michael Artin
, originally in the context of moduli problems, has further enhanced the geometric flexibility of modern algebraic geometry. Grothendieck advocated certain types of ringed toposes as generalisations of schemes, and following his proposals relative schemes over ringed toposes were developed by M. Hakim. Recent ideas about higher algebraic stacks and homotopical or derived algebraic geometry have regard to further expanding the algebraic reach of geometric intuition, bringing algebraic geometry closer in spirit to homotopy theory.
.
In the early days, this was called a prescheme, and a scheme was defined to be a separated prescheme. The term prescheme has fallen out of use, but can still be found in older books, such as Grothendieck's Éléments de géométrie algébrique
and Mumford
's .
if we take as morphisms the morphisms of locally ringed space
s.
Morphisms from schemes to affine schemes are completely understood in terms of ring homomorphisms by the following contravariant adjoint pair: For every scheme X and every commutative ring A we have a natural equivalence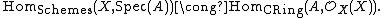
Since Z
is an initial object
in the category of rings
, the category of schemes has Spec(Z) as a final object.
The category of schemes has finite products
, but one has to be careful: the underlying topological space of the product scheme of (X, OX) and (Y, OY) is normally not equal to the product
of the topological spaces X and Y. In fact, the underlying topological space of the product scheme often has more points than the product of the underlying topological spaces. For example, if K is the field with nine elements, then Spec K × Spec K ≈ Spec (K ⊗Z K) ≈ Spec (K ⊗Z/3Z K) ≈ Spec (K × K), a set with two elements, though Spec K has only a single element.
For a scheme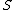
, the category of schemes over 
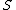has also fibre products, and since it has a final object 
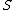, it follows that it has finite limit
s.
, doesn't lose anything.
For detail on the development of scheme theory, which quickly becomes technically demanding, see first glossary of scheme theory
.
are central in commutative algebra
when studying the commutative ring
R, so are the OX-modules central in the study of the scheme X with structure sheaf OX. (See locally ringed space for a definition of OX-modules.) The category of OX-modules is abelian
. Of particular importance are the coherent sheaves
on X, which arise from finitely generated (ordinary) modules on the affine parts of X. The category of coherent sheaves on X is also abelian.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a scheme is an important concept connecting the fields of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. Schemes were introduced by Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
so as to broaden the notion of algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
; some consider schemes to be the basic object of study of modern algebraic geometry. Technically, a scheme is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
together with commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s for all of its open sets, which arises from gluing together spectra
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
(spaces of prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s) of commutative rings along their open subsets.
History and motivation
The algebraic geometers of the Italian schoolItalian school of algebraic geometry
In relation with the history of mathematics, the Italian school of algebraic geometry refers to the work over half a century or more done internationally in birational geometry, particularly on algebraic surfaces. There were in the region of 30 to 40 leading mathematicians who made major...
had often used the somewhat foggy concept of "generic point
Generic point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
" when proving statements about algebraic varieties. What is true for the generic point is true for all points of the variety except a small number of special points. In the 1920s, Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
had first suggested a way to clarify the concept: start with the coordinate ring of the variety (the ring of all polynomial functions defined on the variety); the maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s of this ring will correspond to ordinary points of the variety (under suitable conditions), and the non-maximal prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s will correspond to the various generic points, one for each subvariety. By taking all prime ideals, one thus gets the whole collection of ordinary and generic points. Noether did not pursue this approach.
In the 1930s, Wolfgang Krull
Wolfgang Krull
Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...
turned things around and took a radical step: start with any commutative ring, consider the set of its prime ideals, turn it into a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
by introducing the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
, and study the algebraic geometry of these quite general objects. Others did not see the point of this generality and Krull abandoned it.
André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
was especially interested in algebraic geometry over finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s and other rings. In the 1940s he returned to the prime ideal approach; he needed an abstract variety (outside projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
) for foundational reasons, particularly for the existence in an algebraic setting of the Jacobian variety
Jacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
. In Weil's main foundational book (1946), generic points are constructed by taking points in a very large algebraically closed field, called a universal domain.
In 1944 Oscar Zariski
Oscar Zariski
Oscar Zariski was a Russian mathematician and one of the most influential algebraic geometers of the 20th century.-Education:...
had defined an abstract Zariski–Riemann space
Zariski–Riemann space
In algebraic geometry, a Zariski–Riemann space or Zariski space of a subring k of a field K is a space whose points are valuation rings containing k and properly contained in K...
from the function field of an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, for the needs of birational geometry
Birational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
: this is like a direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of ordinary varieties (under 'blowing up'), and the construction, reminiscent of locale theory, used valuation ring
Valuation ring
In abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
s as points.
In the 1950s, Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
, Claude Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
and Masayoshi Nagata
Masayoshi Nagata
Masayoshi Nagata was a Japanese mathematician, known for his work in the field of commutative algebra....
, motivated largely by the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
relating number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, pursued similar approaches with prime ideals as points. According to Pierre Cartier
Pierre Cartier (mathematician)
Pierre Cartier is a mathematician. An associate of the Bourbaki group and at one time a colleague of Alexander Grothendieck, his interests have ranged over algebraic geometry, representation theory, mathematical physics, and category theory....
, the word scheme was first used in the 1956 Chevalley Seminar, in which Chevalley was pursuing Zariski's ideas; and it was André Martineau who suggested to Serre the move to the current spectrum of a ring
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
in general.
Modern definitions of the objects of algebraic geometry
Alexander GrothendieckAlexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
then gave the decisive definition, bringing to a conclusion a generation of experimental suggestions and partial developments. He defined the spectrum
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
of a commutative ring as the space of prime ideals with Zariski topology, but augments it with a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of rings: to every Zariski-open set he assigns a commutative ring, thought of as the ring of "polynomial functions" defined on that set. These objects are the "affine schemes"; a general scheme is then obtained by "gluing together" several such affine schemes, in analogy to the fact that general varieties can be obtained by gluing together affine varieties.
The generality of the scheme concept was initially criticized: some schemes are removed from having straightforward geometrical interpretation, which made the concept difficult to grasp. However, admitting arbitrary schemes makes the whole category of schemes better-behaved. Moreover, natural considerations regarding, for example, moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
s, lead to schemes which are "non-classical". The occurrence of these schemes that are not varieties (nor built up simply from varieties) in problems that could be posed in classical terms made for the gradual acceptance of the new foundations of the subject.
Subsequent work on algebraic space
Algebraic space
In mathematics, an algebraic space is a generalization of the schemes of algebraic geometry introduced by Michael Artin for use in deformation theory...
s and algebraic stacks by Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
, Mumford
David Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
, and Michael Artin
Michael Artin
Michael Artin is an American mathematician and a professor emeritus in the Massachusetts Institute of Technology mathematics department, known for his contributions to algebraic geometry. and also generally recognized as one of the outstanding professors in his field.Artin was born in Hamburg,...
, originally in the context of moduli problems, has further enhanced the geometric flexibility of modern algebraic geometry. Grothendieck advocated certain types of ringed toposes as generalisations of schemes, and following his proposals relative schemes over ringed toposes were developed by M. Hakim. Recent ideas about higher algebraic stacks and homotopical or derived algebraic geometry have regard to further expanding the algebraic reach of geometric intuition, bringing algebraic geometry closer in spirit to homotopy theory.
Definitions
An affine scheme is a locally ringed space isomorphic to Spec(A) for some commutative ring A. A scheme is a locally ringed space X admitting a covering by open sets Ui, such that the restriction of the structure sheaf OX to each Ui is an affine scheme. Therefore one may think of a scheme as being covered by "coordinate charts" of affine schemes. The above formal definition means exactly that schemes are obtained by glueing together affine schemes for the Zariski topologyZariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
.
In the early days, this was called a prescheme, and a scheme was defined to be a separated prescheme. The term prescheme has fallen out of use, but can still be found in older books, such as Grothendieck's Éléments de géométrie algébrique
Éléments de géométrie algébrique
The Éléments de géométrie algébrique by Alexander Grothendieck , or EGA for short, is a rigorous treatise, in French, on algebraic geometry that was published from 1960 through 1967 by the Institut des Hautes Études Scientifiques...
and Mumford
David Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
's .
The category of schemes
Schemes form a categoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
if we take as morphisms the morphisms of locally ringed space
Ringed space
In mathematics, a ringed space is, intuitively speaking, a space together with a collection of commutative rings, the elements of which are "functions" on each open set of the space...
s.
Morphisms from schemes to affine schemes are completely understood in terms of ring homomorphisms by the following contravariant adjoint pair: For every scheme X and every commutative ring A we have a natural equivalence
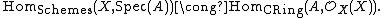
Since Z
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
is an initial object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
in the category of rings
Category of rings
In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms...
, the category of schemes has Spec(Z) as a final object.
The category of schemes has finite products
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
, but one has to be careful: the underlying topological space of the product scheme of (X, OX) and (Y, OY) is normally not equal to the product
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of the topological spaces X and Y. In fact, the underlying topological space of the product scheme often has more points than the product of the underlying topological spaces. For example, if K is the field with nine elements, then Spec K × Spec K ≈ Spec (K ⊗Z K) ≈ Spec (K ⊗Z/3Z K) ≈ Spec (K × K), a set with two elements, though Spec K has only a single element.
For a scheme
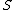, the category of schemes over 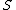has also fibre products, and since it has a final object 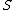, it follows that it has finite limitLimit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
s.
Types of schemes
There are many ways one can qualify a scheme. According to a basic idea of Grothendieck, conditions should be applied to a morphism of schemes. Any scheme S has a unique morphism to Spec(Z), so this attitude, part of the relative point of viewGrothendieck's relative point of view
Grothendieck's relative point of view is a heuristic applied in certain abstract mathematical situations, with a rough meaning of taking for consideration families of 'objects' explicitly depending on parameters, as the basic field of study, rather than a single such object...
, doesn't lose anything.
For detail on the development of scheme theory, which quickly becomes technically demanding, see first glossary of scheme theory
Glossary of scheme theory
This is a glossary of scheme theory. For an introduction to the theory of schemes in algebraic geometry, see affine scheme, projective space, sheaf and scheme. The concern here is to list the fundamental technical definitions and properties of scheme theory...
.
OX modules
Just as the R-modulesModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
are central in commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
when studying the commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R, so are the OX-modules central in the study of the scheme X with structure sheaf OX. (See locally ringed space for a definition of OX-modules.) The category of OX-modules is abelian
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
. Of particular importance are the coherent sheaves
Coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
on X, which arise from finitely generated (ordinary) modules on the affine parts of X. The category of coherent sheaves on X is also abelian.