
Algebraic space
Encyclopedia
In mathematics
, an algebraic space is a generalization of the schemes
of algebraic geometry
introduced by Michael Artin
for use in deformation theory
. Intuitively, an algebraic space is a scheme modulo a "nice" equivalence relation
; the resulting category
of algebraic spaces extends the category of schemes and allows to carry out several natural constructions that are needed for example in deformation theory or in the construction of moduli space
s but are not possible in the smaller category of schemes.
If a third condition
is satisfied, then the algebraic space will be a scheme in the usual sense. Since a general algebraic space does not satisfy this requirement, it allows a single connected component of U to cover X with many "sheets". The point set underlying the algebraic space X is then given by |U| / |R| as a set of equivalence classes.
Let Y be an algebraic space defined by an equivalence relation S ⊂ V × V. The set Hom(Y, X) of morphisms of algebraic spaces is then defined by the condition that it makes the descent sequence

exact (this definition is motivated by a descent theorem of Grothendieck for surjective étale maps of affine schemes). With these definitions, the algebraic spaces form a category
.
Let U be an affine scheme over a field k defined by a system of polynomials g(x), x = (x1, …, xn), let
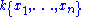
denote the ring
of algebraic function
s in x over k, and let X = {R ⊂ U × U} be an algebraic space.
The appropriate stalks ÕX, x on X are then defined to be the local ring
s of algebraic functions defined by ÕU, u, where u ∈ U is a point lying over x and ÕU, u is the local ring corresponding to u of the ring
of algebraic functions on U.
A point on an algebraic space is said to be smooth if ÕX, x ≅ k{z1, …, zd} for some indeterminate
s z1, …, zd. The dimension of X at x is then just defined to be d.
A morphism f: Y → X of algebraic spaces is said to be étale at y ∈ Y (where x = f(y)) if the induced map on stalks
is an isomorphism.
The structure sheaf OX on the algebraic space X is defined by associating the ring of functions O(V) on V (defined by étale maps from V to the affine line A1 in the sense just defined) to any algebraic space V which is étale over X.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an algebraic space is a generalization of the schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
introduced by Michael Artin
Michael Artin
Michael Artin is an American mathematician and a professor emeritus in the Massachusetts Institute of Technology mathematics department, known for his contributions to algebraic geometry. and also generally recognized as one of the outstanding professors in his field.Artin was born in Hamburg,...
for use in deformation theory
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
. Intuitively, an algebraic space is a scheme modulo a "nice" equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
; the resulting category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of algebraic spaces extends the category of schemes and allows to carry out several natural constructions that are needed for example in deformation theory or in the construction of moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
s but are not possible in the smaller category of schemes.
Definition
An algebraic space X comprises a scheme U and a closed subscheme R ⊂ U × U satisfying the following two conditions:- 1. R is an equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
as a subset of U × U - 2. The projections pi: R → U onto each factor are étale mapÉtale morphismIn algebraic geometry, a field of mathematics, an étale morphism is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem, but because open sets in the Zariski topology are so large, they are not...
s.
If a third condition
- 3. R is the trivial equivalence relation over each connected component of U (i.e. for all x, y belonging to the same connected component of U, we have xRy iff x=y)
is satisfied, then the algebraic space will be a scheme in the usual sense. Since a general algebraic space does not satisfy this requirement, it allows a single connected component of U to cover X with many "sheets". The point set underlying the algebraic space X is then given by |U| / |R| as a set of equivalence classes.
Let Y be an algebraic space defined by an equivalence relation S ⊂ V × V. The set Hom(Y, X) of morphisms of algebraic spaces is then defined by the condition that it makes the descent sequence
Descent (category theory)
In mathematics, the idea of descent has come to stand for a very general idea, extending the intuitive idea of 'gluing' in topology. Since the topologists' glue is actually the use of equivalence relations on topological spaces, the theory starts with some ideas on identification.A sophisticated...

exact (this definition is motivated by a descent theorem of Grothendieck for surjective étale maps of affine schemes). With these definitions, the algebraic spaces form a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
.
Let U be an affine scheme over a field k defined by a system of polynomials g(x), x = (x1, …, xn), let
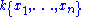
denote the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of algebraic function
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
s in x over k, and let X = {R ⊂ U × U} be an algebraic space.
The appropriate stalks ÕX, x on X are then defined to be the local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
s of algebraic functions defined by ÕU, u, where u ∈ U is a point lying over x and ÕU, u is the local ring corresponding to u of the ring
- k{x1, …, xn} / (g)
of algebraic functions on U.
A point on an algebraic space is said to be smooth if ÕX, x ≅ k{z1, …, zd} for some indeterminate
Indeterminate (variable)
In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...
s z1, …, zd. The dimension of X at x is then just defined to be d.
A morphism f: Y → X of algebraic spaces is said to be étale at y ∈ Y (where x = f(y)) if the induced map on stalks
- ÕX, x → ÕY, y
is an isomorphism.
The structure sheaf OX on the algebraic space X is defined by associating the ring of functions O(V) on V (defined by étale maps from V to the affine line A1 in the sense just defined) to any algebraic space V which is étale over X.
Facts about algebraic spaces
- Algebraic spaces of dimension one (curves) are schemes.
- Non-singular algebraic spaces of dimension two (smooth surfaces) are schemes.
- Group objects in the category of algebraic spaces over a field are schemes.
- Commutative-group objects in the category of algebraic spaces over an arbitrary scheme which are proper, locally finite presentation, flat, and cohomologically flat in dimension 0 are schemes.
- Not every singular algebraic surface is a scheme.
- Not every non-singular 3-dimensional algebraic space is a scheme.
- Every algebraic space contains a dense open affine subscheme, and the complement of such a subscheme always has codimensionCodimensionIn mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
≥ 1. Thus algebraic spaces are in a sense "close" to affine schemes.

