In algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

 (which is a branch of mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

), a prime ideal is a subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

 of a ring

Ring (mathematics)

In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

 which shares many important properties of a prime number

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

 in the ring of integers

Ring of integers

In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...

. The prime ideals for the integers are the sets that contain all the multiples of a given prime number or zero.

Primitive ideal

Primitive ideal

In mathematics, a left primitive ideal in ring theory is the annihilator of a simple left module. A right primitive ideal is defined similarly. Note that left and right primitive ideals are always two-sided ideals....

s are prime, and prime ideals are both primary

Primary ideal

In mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...

 and semiprime.

Prime ideals for commutative rings

An ideal

Ideal (ring theory)

In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....

 P of a commutative ring

Commutative ring

In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....

 R is prime if it has the following two properties:

• If a and b are two elements of R such that their product ab is an element of P, then a is in P or b is in P,
• P is not equal to the whole ring R.

This generalizes the following property of prime numbers: if p is a prime number and if p divides a product ab of two integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s, then p divides a or p divides b. We can therefore say

A positive integer n is a prime number if and only if the ideal nZ is a prime ideal in Z.

Examples

• If R denotes the ring C[X, Y] of polynomial
  Polynomial
  In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
  
  s in two variables with complex
  Complex number
  A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
  
   coefficients, then the ideal generated by the polynomial Y² − X³ − X − 1 is a prime ideal (see elliptic curve
  Elliptic curve
  In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
  
  ).
• In the ring Z[X] of all polynomials with integer coefficients, the ideal generated by 2 and X is a prime ideal. It consists of all those polynomials whose constant coefficient is even.
• In any ring R, a maximal ideal
  Maximal ideal
  In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
  
   is an ideal M that is maximal
  Maximal element
  In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
  
   in the set of all proper ideals of R, i.e. M is contained in
  Subset
  In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
  
   exactly 2 ideals of R, namely M itself and the entire ring R. Every maximal ideal is in fact prime. In a principal ideal domain
  Principal ideal domain
  In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
  
   every nonzero prime ideal is maximal, but this is not true in general.
• If M is a smooth manifold
  Manifold
  In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
  
  , R is the ring of smooth real functions on M, and x is a point in M, then the set of all smooth functions f with f(x) = 0 forms a prime ideal (even a maximal ideal) in R.

Properties

• An ideal I in the ring R is prime if and only if the factor ring R/I is an integral domain. In particular, a commutative ring is an integral domain if and only if {0} is a prime ideal.
• An ideal I is prime if and only if its set-theoretic complement is multiplicatively closed
  Multiplicatively closed set
  In abstract algebra, a subset of a ring is said to be multiplicatively closed if it is closed under multiplication and contains 1 but doesn't contain 0...
  
  .
• Every nonzero ring contains at least one prime ideal (in fact it contains at least one maximal ideal) which is a direct consequence of Krull's theorem
  Krull's theorem
  In mathematics, more specifically in ring theory, Krull's theorem, named after Wolfgang Krull, proves the existence of maximal ideals in any unital ring. The theorem was first stated in 1929 and is equivalent to the axiom of choice.- Krull's theorem :...
  
  .
• The set of all prime ideals (the spectrum of a ring) contains minimal elements (called minimal prime
  Minimal prime (commutative algebra)
  In mathematics, especially in the area of algebra known as commutative algebra, certain prime ideals called minimal prime ideals play an important role in understanding rings and modules...
  
  ). Geometrically, these correspond to irreducible components of the spectrum.
• The preimage of a prime ideal under a ring homomorphism is a prime ideal.
• The sum of two prime ideals is not necessarily prime. For an example, consider the ring 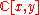with prime ideals and (the ideals generated by and x respectively). Their sum however is not prime: y² − 1 = (y − 1) (y + 1) is in P + Q but its two factors are not. Alternatively, note that the quotient ring has zero divisors so it is not an integral domain and thus cannot be prime.
• In a commutative ring R with at least two elements, if every proper ideal is prime, then the ring is a field. (If the ideal (0) is prime, then the ring R is an integral domain. If q is any non-zero element of R and the ideal 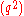is prime, then it contains q and then q is invertible.)
• A nonzero principal ideal is prime if and only if it is generated by a prime element
  Prime element
  In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
  
  . In a UFD, every nonzero prime ideal contains a prime element.

Uses

One use of prime ideals occurs in algebraic geometry

Algebraic geometry

Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...

, where varieties are defined as the zero sets of ideals in polynomial rings. It turns out that the irreducible varieties correspond to prime ideals. In the modern abstract approach, one starts with an arbitrary commutative ring and turns the set of its prime ideals, also called its spectrum

Spectrum of a ring

In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...

, into a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 and can thus define generalizations of varieties called schemes

Scheme (mathematics)

In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...

, which find applications not only in geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, but also in number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

.

The introduction of prime ideals in algebraic number theory

Algebraic number theory

Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...

 was a major step forward: it was realized that the important property of unique factorisation expressed in the fundamental theorem of arithmetic

Fundamental theorem of arithmetic

In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...

 does not hold in every ring of algebraic integer

Algebraic integer

In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...

s, but a substitute was found when Richard Dedekind

Richard Dedekind

Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...

 replaced elements by ideals and prime elements by prime ideals; see Dedekind domain

Dedekind domain

In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...

.

Prime ideals for noncommutative rings

The notion of a prime ideal can be generalized to noncommutative rings by using the commutative definition "ideal-wise". Wolfgang Krull

Wolfgang Krull

Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...

 advanced this idea in 1928. The following content can be found in texts such as and . If R is a (possibly noncommutative) ring and P is an ideal in R other than R itself, we say that P is prime if for any two ideals A and B of R:

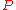• If the product of ideals is contained in , then at least one of and is contained in .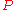

It can be shown that this definition is equivalent to the commutative one in commutative rings. It is readily verified that if an ideal of a noncommutative ring R satisfies the commutative definition of prime, then it also satisfies the noncommutative version. An ideal P satisfying the commutative definition of prime is sometimes called a completely prime ideal to distinguish it from other merely prime ideals in the ring. Completely prime ideals are prime ideals, but the converse is not true. For example, the zero ideal in the ring of n × n matrices over a field is a prime ideal, but it is not completely prime.

This is close to the historical point of view of ideals as ideal number

Ideal number

In number theory an ideal number is an algebraic integer which represents an ideal in the ring of integers of a number field; the idea was developed by Ernst Kummer, and led to Richard Dedekind's definition of ideals for rings...

s, as for the ring Z "A is contained in P" is another way of saying "P divides A", and the unit ideal R represents unity.

Equivalent formulations of the ideal P≠R being prime include the following properties:

• For all a and b in R, (a)(b)⊆P implies a∈P or b∈P.
• For any two right ideals of R, AB⊆P implies A⊆P or B⊆P.
• For any two left ideals of R, AB⊆P implies A⊆P or B⊆P.
• For any elements a and b of R, if aRb⊆P, then a∈P or b∈P.

Prime ideals in commutative rings are characterized by having multiplicatively closed complements in R, and with slight modification, a similar characterization can be formulated for prime ideals in noncommutative rings. A nonempty subset S⊆R is called an m-system if for any a and b in S, there exists r in R such that arb is in S . The following item can then be added to the list of equivalent conditions above:

• The complement R\P is an m-system.

Examples

• Any primitive ideal
  Primitive ideal
  In mathematics, a left primitive ideal in ring theory is the annihilator of a simple left module. A right primitive ideal is defined similarly. Note that left and right primitive ideals are always two-sided ideals....
  
   is prime.

• As with commutative rings, maximal ideals are prime, and also prime ideals contain minimal prime ideals.

• A ring is a prime ring
  Prime ring
  In abstract algebra, a non-trivial ring R is a prime ring if for any two elements a and b of R, arb = 0 for all r in R implies that either a = 0 or b = 0. Prime ring can also refer to the subring of a field determined by its characteristic...
  
   if and only if the zero ideal is a prime ideal, and moreover a ring is a domain if and only if the zero ideal is a completely prime ideal.

• Another fact from commutative theory echoed in noncommutative theory is that if A is a nonzero R module, and P is a maximal element in the poset of annihilator
  Annihilator
  Annihilator may refer to:* Annihilator , a mathematical concept* The annihilator of a vector subspace* Annihilator method, a type of differential operator, used in a particular method for solving differential equations...
  
   ideals of submodules of A, then P is prime.

Important facts

• Prime avoidance lemma: If R is a commutative ring, and A is a subring (possibly without unity), and I₁,...,I_n is a collection of ideals of R with at most two members not prime, then if A is not contained in any I_j, it is also not contained in the union
  Union (set theory)
  In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
  
   of I₁,...,I_n. In particular, A could be an ideal of R.
• If S is any m-system in R, then an lemma essentially due to Krull shows that there exists an ideal of R maximal with respect to being disjoint from S, and moreover the ideal must be prime. In the case {S}={1}, we have Krull's theorem
  Krull's theorem
  In mathematics, more specifically in ring theory, Krull's theorem, named after Wolfgang Krull, proves the existence of maximal ideals in any unital ring. The theorem was first stated in 1929 and is equivalent to the axiom of choice.- Krull's theorem :...
  
  , and this recovers the maximal ideals of R. Another prototypical m-system is the set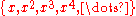 of all positive powers of a non-nilpotent
  Nilpotent
  In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
  
   element.
• For a prime ideal P, the complement R\P has another property beyond being an m-system. If xy is in R\P, then both x and y must be in R\P, since P is an ideal. A set which contains the divisors of its elements is called saturated.
• For a commutative ring R, there is a kind of converse for the previous statement: If S is any nonempty saturated and multiplicatively closed subset of R, the complement R\S is a union of prime ideals of R.
• The union and the intersection of a chain of prime ideals is a prime ideal. With Zorn's Lemma
  Zorn's lemma
  Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
  
  , this implies that the poset of prime ideals (partially ordered by inclusion) has maximal and minimal elements.

Connection to maximality

Prime ideals can frequently be produced as maximal elements of certain collections of ideals. For example:

• An ideal maximal with respect to having empty intersection with a fixed m-sytstem is prime.
• An ideal maximal among annihilator
  Annihilator
  Annihilator may refer to:* Annihilator , a mathematical concept* The annihilator of a vector subspace* Annihilator method, a type of differential operator, used in a particular method for solving differential equations...
  
  s of submodules of a fixed R module M is prime.
• In a commutative ring, an ideal maximal with respect to being non-principal is prime.
• In a commutative ring, an ideal maximal with respect to being not countably generated is prime.

This unusual affinity has been studied further in .