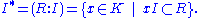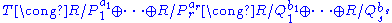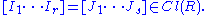Dedekind domain
Encyclopedia
In abstract algebra
, a Dedekind domain or Dedekind ring, named after Richard Dedekind
, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors. There are at least three other characterizations of Dedekind domains which are sometimes taken as the definition: see below.
Note that a field is a commutative ring in which there are no nontrivial proper ideals, so that any field is a Dedekind domain, however in a rather vacuous way. Some authors add the requirement that a Dedekind domain not be a field. Many more authors state theorems for Dedekind domains with the implicit proviso that they may require trivial modifications for the case of fields.
An immediate consequence of the definition is that every principal ideal domain
(PID) is a Dedekind domain. In fact a Dedekind domain is a unique factorization domain
(UFD) iff it is a PID.
. In the attempt to determine which integers are represented by the quadratic form 
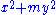, it is natural to factor the quadratic form into 
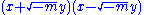, the factorization taking place in the ring of integers of the quadratic field 
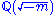. Similarly, for a positive integer 
the polynomial 
(which is relevant for solving the Fermat equation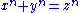 
) can be factored over the ring 
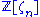, where 
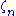is a primitive 
root of unity.
For a few small values of
and 
these rings of algebraic integers are PIDs, and this can be seen as an explanation of the classical successes of Fermat
(
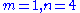) and Euler
(
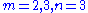). By this time a procedure for determining whether the ring of all algebraic integers
of a given quadratic field
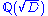is a PID was well known to the quadratic form
theorists. Especially, Gauss
had looked at the case of imaginary quadratic fields: he found exactly nine values of
for which the ring of integers is a PID and conjectured that there are no further values. (Gauss' conjecture was proven more than one hundred years later by Heegner, Baker and Stark.) However, this was understood (only) in the language of equivalence classes of quadratic forms, so that in particular the analogy between quadratic forms and the Fermat equation seems not to have been perceived. In 1847 Gabriel Lamé
announced a solution of Fermat's Last Theorem
for all
-- i.e., that the Fermat equation has no solutions in nonzero integers, but it turned out that his solution hinged on the assumption that the cyclotomic ring 
is a UFD. Ernst Kummer
had shown three years before that this was not the case already for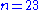
(the full, finite list of values for which 
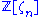is a UFD is now known). At the same time, Kummer developed powerful new methods to prove Fermat's Last Theorem at least for a large class of prime exponents 
using what we now recognize as the fact that the ring 
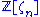is a Dedekind domain. In fact Kummer worked not with ideals but with "ideal numbers", and the modern definition of an ideal was given by Dedekind.
By the 20th century, algebraists and number theorists had come to realize that the condition of being a PID is rather delicate, whereas the condition of being a Dedekind domain is quite robust. For instance the ring of ordinary integers is a PID, but as seen above the ring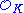
of algebraic integers in a number field 
need not be a PID. In fact, although Gauss also conjectured that there are infinitely many primes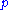 
such that the ring of integers of 
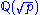is a PID, to this day we do not even know whether there are infinitely many number fields 
(of arbitrary degree) such that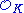 
is a PID! On the other hand, the ring of integers in a number field is always a Dedekind domain.
Another illustration of the delicate/robust dichotomy is the fact that being a Dedekind domain is, among Noetherian domains, a local property -- a Noetherian domain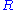
is Dedekind iff for every maximal ideal
of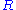 
the localization
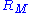is a Dedekind ring. But a local domain
is a Dedekind ring iff it is a PID iff it is a discrete valuation ring
(DVR), so the same local characterization cannot hold for PIDs: rather, one may say that the concept of a Dedekind ring is the globalization of that of a DVR.
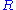which is not a field
, all of the following conditions are equivalent:
(DD1) Every nonzero proper ideal factors into primes.
(DD2)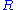
is Noetherian
, and the localization at each maximal ideal is a Discrete Valuation Ring.
(DD3) Every fractional ideal
of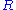
is invertible.
(DD4)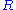
is an integrally closed, Noetherian domain
with Krull dimension
one (i.e., every nonzero prime ideal is maximal).
Thus a Dedekind domain is a domain which satisfies any one, and hence all four, of (DD1) through (DD4). Which of these conditions one takes as the definition is therefore merely a matter of taste. In practice, it is often easiest to verify (DD4).
s and therefore all discrete valuation ring
s are Dedekind domains.
The ring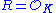
of algebraic integers in a number field K is Noetherian, integrally closed, and of dimension one (to see the last property, observe that for any nonzero ideal I of R, R/I is finite and recall that a finite integral domain is a field), so by (DD4) R is a Dedekind domain. As above, this includes all the examples considered by Kummer and Dedekind and was the motivating case for the general definition, and these remain among the most studied examples.
The other class of Dedekind rings which is arguably of equal importance comes from geometry: let C be a nonsingular geometrically integral affine algebraic curve
over a field k. Then the coordinate ring k[C] of regular functions on C is a Dedekind domain. Indeed, this is essentially an algebraic translation of these geometric terms: the coordinate ring of any affine variety is, by definition, a finitely generated k-algebra, so Noetherian; moreover curve means dimension one and nonsingular implies (and, in dimension one, is equivalent to) normal, which by definition means integrally closed.
Both of these constructions can be viewed as special cases of the following basic result:
Theorem: Let R be a Dedekind domain with fraction field
K. Let L be a finite degree field extension
of K and denote by S the integral closure of R in L. Then S is itself a Dedekind domain.
Applying this theorem when R is itself a PID gives us a way of building Dedekind domains out of PIDs. Taking R = Z this construction tells us precisely that rings of integers of number fields are Dedekind domains. Taking R = k[t] gives us the above case of nonsingular affine curves.
Zariski
and Samuel
were sufficiently taken by this construction to pose as a question whether every Dedekind domain arises in such a fashion, i.e., by starting with a PID and taking the integral closure in a finite degree field extension. A surprisingly simple negative answer was given by L. Claborn.
If the situation is as above but the extension L of K is algebraic of infinite degree, then it is still possible for the integral closure S of R in L to be a Dedekind domain, but it is not guaranteed. For example, take again R = Z, K = Q and now take L to be the field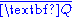
of all algebraic number
s. The integral closure is nothing else than the ring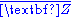
of all algebraic integers. Since the square root of an algebraic integer is again an algebraic integer, it is not possible to factor any nonzero nonunit algebraic integer into a finite product of irreducible elements, which implies that 
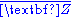is not Noetherian! In general, the integral closure of a Dedekind domain in an infinite algebraic extension is a Prüfer domain
; it turns out that the ring of algebraic integers is slightly more special than this: it is a Bézout domain
.
is a nonzero R-submodule I of K for which there exists a nonzero x in K such that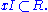
(We remark that this is not exactly the same as the definition given on the page describing fractional ideals: the definition given there is that a fractional ideal is a nonzero finitely generated R-submodule of K. The two definitions are equivalent if and only if R is Noetherian. Otherwise our definition is strictly weaker, being permissive enough to make all nonzero R-submodules of R — i.e., integral ideals — fractional ideals.)
Given two fractional ideals I and J, one defines their product IJ as the set of all finite sums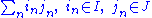
: the product IJ is again a fractional ideal. The set Frac(R) of all fractional ideals endowed with the above product is a commutative semigroup and in fact a monoid: the identity element is the fractional ideal R.
For any fractional ideal I, one may define the fractional ideal
One then tautologically has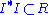
. In fact one has equality if and only if I, as an element of the monoid of Frac(R), is invertible. In other words, if I has any inverse, then the inverse must be 
.
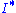A principal fractional ideal is one of the form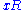
for some nonzero x in K. Note that each principal fractional ideal is invertible, the inverse of 
being simply 
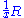. We denote the subgroup of principal fractional ideals by Prin(R).
A domain R is a PID if and only if every fractional ideal is principal. In this case, we have Frac(R) = Prin(R) =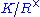
, since two principal fractional ideals 
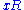and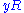 
are equal iff 
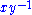is a unit in R.
For a general domain R, it is meaningful to take the quotient of the monoid Frac(R) of all fractional ideals by the submonoid Prin(R) of principal fractional ideals. However this quotient itself is generally only a monoid. In fact it is easy to see that the class of a fractional ideal I in Frac(R)/Prin(R) is invertible if and only if I itself is invertible.
Now we can appreciate (DD3): in a Dedekind domain—and only in a Dedekind domain! -- is every fractional ideal invertible. Thus these are precisely the class of domains for which Frac(R)/Prin(R) forms a group, the ideal class group
Cl(R) of R. This group is trivial if and only if R is a PID, so can be viewed as quantifying the obstruction to a general Dedekind domain being a PID.
We note that for an arbitrary domain one may define the Picard group Pic(R) as the group of invertible fractional ideals Inv(R) modulo the subgroup of principal fractional ideals. For a Dedekind domain this is of course the same as the ideal class group. However, on a more general class of domains—including Noetherian domains and Krull domains -- the ideal class group is constructed in a different way, and there is a canonical homomorphism
which is however generally neither injective nor surjective. This is an affine analogue of the distinction between Cartier divisors and Weil divisors on a singular algebraic variety.
A remarkable theorem of L. Claborn (Claborn 1966) asserts that for any abelian group G whatsoever, there exists a Dedekind domain R whose ideal class group is isomorphic to G. Later, C.R. Leedham-Green
showed that such an R may constructed as the integral closure of a PID in a quadratic field extension (Leedham-Green 1972). In 1976, M. Rosen showed how to realize any countable abelian group as the class group of a Dedekind domain which is a subring of the rational function field of an elliptic curve, and conjectured that such an "elliptic" construction should be possible for a general abelian group (Rosen 1976). Rosen's conjecture was proven in 2008 by P.L. Clark (Clark 2009).
In contrast, one of the basic theorems in algebraic number theory asserts that the class group of the ring of integers of a number field is finite; its cardinality is called the class number and it is an important and rather mysterious invariant, notwithstanding the hard work of many leading mathematicians from Gauss to the present day.
(PID), it is natural to ask for a corresponding theory for finitely generated modules over a Dedekind domain.
Let us briefly recall the structure theory in the case of a finitely generated module
over a PID 
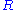. We define the torsion submodule 
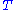to be the set of elements 
of 
such that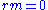 
for some nonzero 
in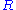 
. Then:
(M1)
can be decomposed into a direct sum
of cyclic
torsion modules, each of the form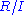
for some nonzero ideal 
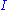of 
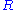. By the Chinese Remainder Theorem, each 
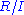can further be decomposed into a direct sum of submodules of the form 
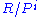, where 
is a power of a prime ideal. This decomposition need not be unique, but any two decompositions
differ only in the order of the factors.
(M2) The torsion submodule is a direct summand: i.e., there exists a complementary submodule
of 
such that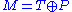 
.
(M3PID)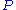
isomorphic to 
for a uniquely determined non-negative integer 
. In particular, 
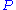a finitely generated free module.
Now let
be a finitely generated module over an arbitrary Dedekind domain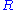 
. Then (M1) and (M2) hold verbatim. However, it follows from (M3PID) that a finitely generated torsionfree module 
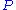over a PID is free. In particular, it asserts that all fractional ideals are principal, a statement which is false whenever 
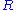is not a PID. In other words, the nontriviality of the class group Cl(R) causes (M3PID) to fail. Remarkably, the additional structure in torsionfree finitely generated modules over an arbitrary Dedekind domain is precisely controlled by the class group, as we now explain. Over an arbitrary Dedekind domain one has
(M3DD)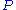
is isomorphic to a direct sum of rank one projective module
s: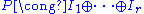
. Moreover, for any rank one projective modules 
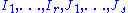, one has
if and only if
and
Rank one projective modules can be identified with fractional ideals, and the last condition can be rephrased as
Thus a finitely generated torsionfree module of rank
can be expressed as 
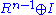, where 
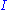is a rank one projective module. The class 
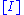of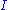 
in Cl(R) is uniquely determined. A consequence of this is:
Theorem: Let R be a Dedekind domain. Then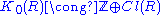
, where K0(R) is the Grothendieck group
of the commutative monoid of finitely generated projective R modules.
These results were established by Ernst Steinitz
in 1912.
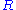which are locally but not globally Dedekind: the localization of 
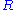at each maximal ideal is a Dedekind ring (equivalently, a DVR
) but
itself is not Dedekind. As mentioned above, such a ring cannot be Noetherian. It seems that the first examples of such rings were constructed by N. Nakano in 1953. In the literature such rings are sometimes called "proper almost Dedekind rings."
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a Dedekind domain or Dedekind ring, named after Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors. There are at least three other characterizations of Dedekind domains which are sometimes taken as the definition: see below.
Note that a field is a commutative ring in which there are no nontrivial proper ideals, so that any field is a Dedekind domain, however in a rather vacuous way. Some authors add the requirement that a Dedekind domain not be a field. Many more authors state theorems for Dedekind domains with the implicit proviso that they may require trivial modifications for the case of fields.
An immediate consequence of the definition is that every principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
(PID) is a Dedekind domain. In fact a Dedekind domain is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
(UFD) iff it is a PID.
The prehistory of Dedekind domains
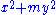In the 19th century it became a common technique to gain insight into integral solutions of polynomial equations (i.e., Diophantine equations) using rings of algebraic numbers of higher degree. For instance, fix a positive integer. In the attempt to determine which integers are represented by the quadratic form , it is natural to factor the quadratic form into 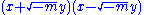, the factorization taking place in the ring of integers of the quadratic field . Similarly, for a positive integer the polynomial (which is relevant for solving the Fermat equation 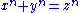) can be factored over the ring 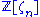, where 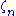is a primitive root of unity.For a few small values of
and these rings of algebraic integers are PIDs, and this can be seen as an explanation of the classical successes of FermatPierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
(
) and EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
(
). By this time a procedure for determining whether the ring of all algebraic integersQuadratic integer
In number theory, quadratic integers are a generalization of the rational integers to quadratic fields. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.- Definition :Quadratic...
of a given quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
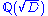is a PID was well known to the quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
theorists. Especially, Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
had looked at the case of imaginary quadratic fields: he found exactly nine values of
for which the ring of integers is a PID and conjectured that there are no further values. (Gauss' conjecture was proven more than one hundred years later by Heegner, Baker and Stark.) However, this was understood (only) in the language of equivalence classes of quadratic forms, so that in particular the analogy between quadratic forms and the Fermat equation seems not to have been perceived. In 1847 Gabriel LaméGabriel Lamé
Gabriel Léon Jean Baptiste Lamé was a French mathematician.-Biography:Lamé was born in Tours, in today's département of Indre-et-Loire....
announced a solution of Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
for all
-- i.e., that the Fermat equation has no solutions in nonzero integers, but it turned out that his solution hinged on the assumption that the cyclotomic ring is a UFD. Ernst KummerErnst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
had shown three years before that this was not the case already for
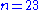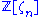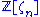(the full, finite list of values for which is a UFD is now known). At the same time, Kummer developed powerful new methods to prove Fermat's Last Theorem at least for a large class of prime exponents using what we now recognize as the fact that the ring is a Dedekind domain. In fact Kummer worked not with ideals but with "ideal numbers", and the modern definition of an ideal was given by Dedekind.By the 20th century, algebraists and number theorists had come to realize that the condition of being a PID is rather delicate, whereas the condition of being a Dedekind domain is quite robust. For instance the ring of ordinary integers is a PID, but as seen above the ring
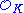of algebraic integers in a number field need not be a PID. In fact, although Gauss also conjectured that there are infinitely many primes 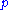such that the ring of integers of 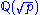is a PID, to this day we do not even know whether there are infinitely many number fields (of arbitrary degree) such that 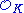is a PID! On the other hand, the ring of integers in a number field is always a Dedekind domain.Another illustration of the delicate/robust dichotomy is the fact that being a Dedekind domain is, among Noetherian domains, a local property -- a Noetherian domain
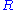is Dedekind iff for every maximal idealMaximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
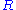of the localizationLocalization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
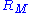is a Dedekind ring. But a local domainLocal ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
is a Dedekind ring iff it is a PID iff it is a discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
(DVR), so the same local characterization cannot hold for PIDs: rather, one may say that the concept of a Dedekind ring is the globalization of that of a DVR.
Alternative definitions
For an integral domain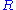 which is not a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, all of the following conditions are equivalent:
(DD1) Every nonzero proper ideal factors into primes.
(DD2)
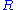is NoetherianNoetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
, and the localization at each maximal ideal is a Discrete Valuation Ring.
(DD3) Every fractional ideal
Fractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
of
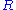is invertible.(DD4)
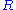is an integrally closed, Noetherian domainNoetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
with Krull dimension
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
one (i.e., every nonzero prime ideal is maximal).
Thus a Dedekind domain is a domain which satisfies any one, and hence all four, of (DD1) through (DD4). Which of these conditions one takes as the definition is therefore merely a matter of taste. In practice, it is often easiest to verify (DD4).
Some examples of Dedekind domains
All principal ideal domainPrincipal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
s and therefore all discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
s are Dedekind domains.
The ring
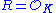of algebraic integers in a number field K is Noetherian, integrally closed, and of dimension one (to see the last property, observe that for any nonzero ideal I of R, R/I is finite and recall that a finite integral domain is a field), so by (DD4) R is a Dedekind domain. As above, this includes all the examples considered by Kummer and Dedekind and was the motivating case for the general definition, and these remain among the most studied examples.The other class of Dedekind rings which is arguably of equal importance comes from geometry: let C be a nonsingular geometrically integral affine algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
over a field k. Then the coordinate ring k[C] of regular functions on C is a Dedekind domain. Indeed, this is essentially an algebraic translation of these geometric terms: the coordinate ring of any affine variety is, by definition, a finitely generated k-algebra, so Noetherian; moreover curve means dimension one and nonsingular implies (and, in dimension one, is equivalent to) normal, which by definition means integrally closed.
Both of these constructions can be viewed as special cases of the following basic result:
Theorem: Let R be a Dedekind domain with fraction field
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
K. Let L be a finite degree field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of K and denote by S the integral closure of R in L. Then S is itself a Dedekind domain.
Applying this theorem when R is itself a PID gives us a way of building Dedekind domains out of PIDs. Taking R = Z this construction tells us precisely that rings of integers of number fields are Dedekind domains. Taking R = k[t] gives us the above case of nonsingular affine curves.
Zariski
Oscar Zariski
Oscar Zariski was a Russian mathematician and one of the most influential algebraic geometers of the 20th century.-Education:...
and Samuel
Pierre Samuel
Pierre Samuel was a French mathematician, known for his work in commutative algebra and its applications to algebraic geometry. The two-volume work Commutative Algebra that he wrote with Oscar Zariski is a classic. Other books of his covered projective geometry and algebraic number theory...
were sufficiently taken by this construction to pose as a question whether every Dedekind domain arises in such a fashion, i.e., by starting with a PID and taking the integral closure in a finite degree field extension. A surprisingly simple negative answer was given by L. Claborn.
If the situation is as above but the extension L of K is algebraic of infinite degree, then it is still possible for the integral closure S of R in L to be a Dedekind domain, but it is not guaranteed. For example, take again R = Z, K = Q and now take L to be the field
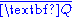of all algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s. The integral closure is nothing else than the ring
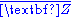of all algebraic integers. Since the square root of an algebraic integer is again an algebraic integer, it is not possible to factor any nonzero nonunit algebraic integer into a finite product of irreducible elements, which implies that 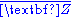is not Noetherian! In general, the integral closure of a Dedekind domain in an infinite algebraic extension is a Prüfer domainPrüfer domain
In mathematics, a Prüfer domain is a type of commutative ring that generalizes Dedekind domains in a non-Noetherian context. These rings possess the nice ideal and module theoretic properties of Dedekind domains, but usually only for finitely generated modules...
; it turns out that the ring of algebraic integers is slightly more special than this: it is a Bézout domain
Bézout domain
In mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
.
Fractional ideals and the class group
Let R be an integral domain with fraction field K. A fractional idealFractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
is a nonzero R-submodule I of K for which there exists a nonzero x in K such that
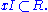
(We remark that this is not exactly the same as the definition given on the page describing fractional ideals: the definition given there is that a fractional ideal is a nonzero finitely generated R-submodule of K. The two definitions are equivalent if and only if R is Noetherian. Otherwise our definition is strictly weaker, being permissive enough to make all nonzero R-submodules of R — i.e., integral ideals — fractional ideals.)
Given two fractional ideals I and J, one defines their product IJ as the set of all finite sums
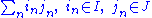: the product IJ is again a fractional ideal. The set Frac(R) of all fractional ideals endowed with the above product is a commutative semigroup and in fact a monoid: the identity element is the fractional ideal R.For any fractional ideal I, one may define the fractional ideal
One then tautologically has
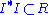. In fact one has equality if and only if I, as an element of the monoid of Frac(R), is invertible. In other words, if I has any inverse, then the inverse must be 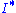.A principal fractional ideal is one of the form
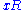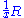for some nonzero x in K. Note that each principal fractional ideal is invertible, the inverse of being simply . We denote the subgroup of principal fractional ideals by Prin(R).A domain R is a PID if and only if every fractional ideal is principal. In this case, we have Frac(R) = Prin(R) =
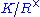, since two principal fractional ideals 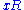and 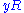are equal iff 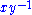is a unit in R.For a general domain R, it is meaningful to take the quotient of the monoid Frac(R) of all fractional ideals by the submonoid Prin(R) of principal fractional ideals. However this quotient itself is generally only a monoid. In fact it is easy to see that the class of a fractional ideal I in Frac(R)/Prin(R) is invertible if and only if I itself is invertible.
Now we can appreciate (DD3): in a Dedekind domain—and only in a Dedekind domain! -- is every fractional ideal invertible. Thus these are precisely the class of domains for which Frac(R)/Prin(R) forms a group, the ideal class group
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
Cl(R) of R. This group is trivial if and only if R is a PID, so can be viewed as quantifying the obstruction to a general Dedekind domain being a PID.
We note that for an arbitrary domain one may define the Picard group Pic(R) as the group of invertible fractional ideals Inv(R) modulo the subgroup of principal fractional ideals. For a Dedekind domain this is of course the same as the ideal class group. However, on a more general class of domains—including Noetherian domains and Krull domains -- the ideal class group is constructed in a different way, and there is a canonical homomorphism
- Pic(R)
Cl(R)
which is however generally neither injective nor surjective. This is an affine analogue of the distinction between Cartier divisors and Weil divisors on a singular algebraic variety.
A remarkable theorem of L. Claborn (Claborn 1966) asserts that for any abelian group G whatsoever, there exists a Dedekind domain R whose ideal class group is isomorphic to G. Later, C.R. Leedham-Green
Charles Leedham-Green
Charles R. Leedham-Green is a retired professor of mathematics at Queen Mary, University of London, known for his work in group theory. He completed his DPhil at the University of Oxford....
showed that such an R may constructed as the integral closure of a PID in a quadratic field extension (Leedham-Green 1972). In 1976, M. Rosen showed how to realize any countable abelian group as the class group of a Dedekind domain which is a subring of the rational function field of an elliptic curve, and conjectured that such an "elliptic" construction should be possible for a general abelian group (Rosen 1976). Rosen's conjecture was proven in 2008 by P.L. Clark (Clark 2009).
In contrast, one of the basic theorems in algebraic number theory asserts that the class group of the ring of integers of a number field is finite; its cardinality is called the class number and it is an important and rather mysterious invariant, notwithstanding the hard work of many leading mathematicians from Gauss to the present day.
Finitely generated modules over a Dedekind domain
In view of the well known and exceedingly useful structure theorem for finitely generated modules over a principal ideal domainStructure theorem for finitely generated modules over a principal ideal domain
In mathematics, in the field of abstract algebra, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in...
(PID), it is natural to ask for a corresponding theory for finitely generated modules over a Dedekind domain.
Let us briefly recall the structure theory in the case of a finitely generated module
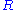over a PID . We define the torsion submodule 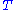to be the set of elements of such that 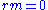for some nonzero in 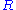. Then:(M1)
can be decomposed into a direct sumDirect sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of cyclic
Cyclic module
In mathematics, more specifically in ring theory, a cyclic module is a module over a ring which is generated by one element. The term is by analogy with cyclic groups, that is groups which are generated by one element.- Definition :...
torsion modules, each of the form
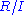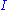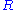for some nonzero ideal of . By the Chinese Remainder Theorem, each 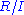can further be decomposed into a direct sum of submodules of the form 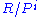, where is a power of a prime ideal. This decomposition need not be unique, but any two decompositions
differ only in the order of the factors.
(M2) The torsion submodule is a direct summand: i.e., there exists a complementary submodule
of such that 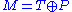.(M3PID)
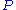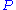isomorphic to for a uniquely determined non-negative integer . In particular, a finitely generated free module.Now let
be a finitely generated module over an arbitrary Dedekind domain 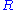. Then (M1) and (M2) hold verbatim. However, it follows from (M3PID) that a finitely generated torsionfree module 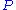over a PID is free. In particular, it asserts that all fractional ideals are principal, a statement which is false whenever 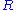is not a PID. In other words, the nontriviality of the class group Cl(R) causes (M3PID) to fail. Remarkably, the additional structure in torsionfree finitely generated modules over an arbitrary Dedekind domain is precisely controlled by the class group, as we now explain. Over an arbitrary Dedekind domain one has(M3DD)
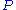is isomorphic to a direct sum of rank one projective moduleProjective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
s:
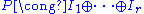. Moreover, for any rank one projective modules 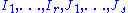, one has
if and only if
and
Rank one projective modules can be identified with fractional ideals, and the last condition can be rephrased as
Thus a finitely generated torsionfree module of rank
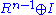can be expressed as , where 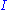is a rank one projective module. The class 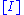of 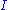in Cl(R) is uniquely determined. A consequence of this is:Theorem: Let R be a Dedekind domain. Then
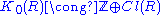, where K0(R) is the Grothendieck groupGrothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
of the commutative monoid of finitely generated projective R modules.
These results were established by Ernst Steinitz
Ernst Steinitz
Ernst Steinitz was a German mathematician.- Biography :Steinitz was born in Laurahütte , Silesia, Germany , the son of Sigismund Steinitz, a Jewish coal merchant, and his wife Auguste Cohen; he had two brothers. He studied at the University of Breslau and the University of Berlin, receiving his Ph.D...
in 1912.
Locally Dedekind rings
There exist integral domains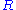 which are locally but not globally Dedekind: the localization of 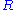at each maximal ideal is a Dedekind ring (equivalently, a DVRDiscrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
) but
itself is not Dedekind. As mentioned above, such a ring cannot be Noetherian. It seems that the first examples of such rings were constructed by N. Nakano in 1953. In the literature such rings are sometimes called "proper almost Dedekind rings."