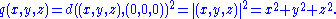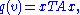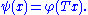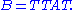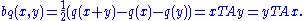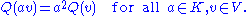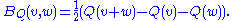Quadratic form
Encyclopedia
In mathematics
, a quadratic form is a homogeneous polynomial
of degree
two in a number of variables. For example,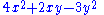
is a quadratic form in the variables x and y.
Quadratic forms occupy a central place in various branches of mathematics, including number theory
, linear algebra
, group theory
(orthogonal group
), differential geometry (Riemannian metric), differential topology
(intersection forms
of four-manifolds), and Lie theory
(the Killing form
).
In the cases of one, two, and three variables they are called unary, binary
, and ternary and have the following explicit form:
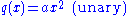
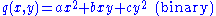
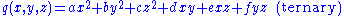 ,
,
where a,…,f are the coefficients. Note that quadratic function
s, such as ax2+bx+c in the one variable case, are not quadratic forms, as they are typically not homogeneous
(unless b and c are both 0).
The theory of quadratic forms and methods used in their study depend in a large measure on the nature of the coefficients, which may be real
or complex
numbers, rational number
s, or integer
s. In linear algebra
, analytic geometry
, and in the majority of applications of quadratic forms, the coefficients are real or complex numbers. In the algebraic theory of quadratic forms, the coefficients are elements of a certain field. In the arithmetic theory of quadratic forms, the coefficients belong to a fixed commutative ring
, frequently the integers Z or the p-adic integers Zp. Binary quadratic forms have been extensively studied in number theory
, in particular, in the theory of quadratic field
s, continued fraction
s, and modular forms. The theory of integral quadratic forms in n variables has important applications to algebraic topology
.
Using homogeneous coordinates
, a non-zero quadratic form in n variables defines an (n−2)-dimensional quadric
in the (n−1)-dimensional projective space
. This is a basic construction in projective geometry
. In this way one may visualize 3-dimensional real quadratic forms as conic sections.
A closely related notion with geometric overtones is a quadratic space, which is a pair (V,q), with V a vector space
over a field k, and q:V → k a quadratic form on V. An example is given by the three-dimensional Euclidean space
and the square of the Euclidean norm expressing the distance
between a point with coordinates (x,y,z) and the origin:
 , where
, where  are integers. This problem is related to the problem of finding Pythagorean triple
are integers. This problem is related to the problem of finding Pythagorean triple
s, which appeared in the second millennium B.C.
In 628, the Indian mathematician Brahmagupta
wrote Brahmasphutasiddhanta
which includes, among many other things, a study of equations of the form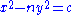 . In particular he considered what is now called Pell's equation
. In particular he considered what is now called Pell's equation
,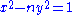 , and found a method for its solution. In Europe this problem was studied by Brouncker
, and found a method for its solution. In Europe this problem was studied by Brouncker
, Euler
and Lagrange
.
In 1801 Gauss
published Disquisitiones Arithmeticae
, a major portion of which was devoted to a complete theory of binary quadratic form
s over the integer
s. Since then, the concept has been generalized, and the connections with quadratic number fields, the modular group
, and other areas of mathematics have been further elucidated.
Conversely, given a quadratic form in n variables, its coefficients can be arranged into an n×n symmetric matrix. One of the most important questions in the theory of quadratic forms is how much can one simplify a quadratic form q by a homogeneous linear change of variables. A fundamental theorem due to Jacobi asserts that q can be brought to a diagonal form
so that the corresponding symmetric matrix is diagonal
, and this is even possible to accomplish with a change of variables given by an orthogonal matrix
– in this case the coefficients λ1, λ2, …, λn are in fact determined uniquely up to a permutation. If the change of variables is given by an invertible matrix, not necessarily orthogonal, then the coefficients λi can be made to be 0,1, and −1. Sylvester's law of inertia
states that the numbers of 1 and −1 are invariants
of the quadratic form, in the sense that any other diagonalization will contain them in the same quantities. The signature of the quadratic form is the triple (n0, n+, n−) where n0 is the number 0s and n± is the number of ±1s. Sylvester's law of inertia shows that this is a well-defined quantity attached to the quadratic form. The case when all λi have the same sign is especially important: in this case the quadratic form is called positive definite (all 1) or negative definite (all −1); if none of the terms are 0 then the form is called ; this includes positive definite, negative definite, and indefinite (a mix of 1 and −1); equivalently, a nondegenerate quadratic form is one whose associated symmetric form is a nondegenerate bilinear form. A real vector space with an indefinite nondegenerate quadratic form of index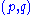 (p 1s, q −1s) is often denoted as
(p 1s, q −1s) is often denoted as 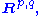 particularly in the physical theory of space-time.
particularly in the physical theory of space-time.
Below we reformulate these results in a different way.
Let q be a quadratic form defined on an n-dimensional real
vector space. Let A be the matrix of the quadratic form q in a given basis. This means that A is a symmetric n×n matrix such that
where x is the column vector of coordinates of v in the chosen basis. Under a change of basis, the column x is multiplied on the left by an n×n invertible matrix S, and the symmetric square matrix A is transformed into another symmetric square matrix B of the same size according to the formula
Any symmetric matrix A can be transformed into a diagonal matrix
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quadratic form is a homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
two in a number of variables. For example,
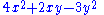
is a quadratic form in the variables x and y.
Quadratic forms occupy a central place in various branches of mathematics, including number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
(orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
), differential geometry (Riemannian metric), differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
(intersection forms
Intersection form (4-manifold)
In mathematics, the intersection form of an oriented compact 4-manifold is a special symmetric bilinear form on the 2nd cohomology group of the 4-manifold...
of four-manifolds), and Lie theory
Lie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
(the Killing form
Killing form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
).
Introduction
Quadratic forms are homogeneous quadratic polynomials in n variables.In the cases of one, two, and three variables they are called unary, binary
Binary quadratic form
In mathematics, a binary quadratic form is a quadratic form in two variables. More concretely, it is a homogeneous polynomial of degree 2 in two variableswhere a, b, c are the coefficients...
, and ternary and have the following explicit form:
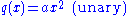
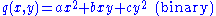
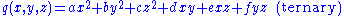 ,
,where a,…,f are the coefficients. Note that quadratic function
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
s, such as ax2+bx+c in the one variable case, are not quadratic forms, as they are typically not homogeneous
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
(unless b and c are both 0).
The theory of quadratic forms and methods used in their study depend in a large measure on the nature of the coefficients, which may be real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers, rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, or integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, and in the majority of applications of quadratic forms, the coefficients are real or complex numbers. In the algebraic theory of quadratic forms, the coefficients are elements of a certain field. In the arithmetic theory of quadratic forms, the coefficients belong to a fixed commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, frequently the integers Z or the p-adic integers Zp. Binary quadratic forms have been extensively studied in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, in particular, in the theory of quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
s, continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s, and modular forms. The theory of integral quadratic forms in n variables has important applications to algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
.
Using homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
, a non-zero quadratic form in n variables defines an (n−2)-dimensional quadric
Quadric (projective geometry)
In projective geometry a quadric is the set of points of a projective space where a certain quadratic form on the homogeneous coordinates becomes zero...
in the (n−1)-dimensional projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. This is a basic construction in projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
. In this way one may visualize 3-dimensional real quadratic forms as conic sections.
A closely related notion with geometric overtones is a quadratic space, which is a pair (V,q), with V a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field k, and q:V → k a quadratic form on V. An example is given by the three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and the square of the Euclidean norm expressing the distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between a point with coordinates (x,y,z) and the origin:
History
The study of particular quadratic forms, in particular the question of whether a given integer can be the value of a quadratic form over the integers, dates back many centuries. One such case is Fermat's theorem on sums of two squares, which determines when an integer may be expressed in the form , where
, where  are integers. This problem is related to the problem of finding Pythagorean triple
are integers. This problem is related to the problem of finding Pythagorean triplePythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
s, which appeared in the second millennium B.C.
In 628, the Indian mathematician Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
wrote Brahmasphutasiddhanta
Brahmasphutasiddhanta
The main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
which includes, among many other things, a study of equations of the form
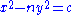 . In particular he considered what is now called Pell's equation
. In particular he considered what is now called Pell's equationPell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
,
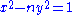 , and found a method for its solution. In Europe this problem was studied by Brouncker
, and found a method for its solution. In Europe this problem was studied by BrounckerWilliam Brouncker, 2nd Viscount Brouncker
William Brouncker, 2nd Viscount Brouncker, PRS was an English mathematician.Brouncker obtained a DM at the University of Oxford in 1647. He was one of the founders and the first President of the Royal Society. In 1662, he became Chancellor to Queen Catherine, then chief of the Saint Catherine's...
, Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
and Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
.
In 1801 Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
published Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
, a major portion of which was devoted to a complete theory of binary quadratic form
Binary quadratic form
In mathematics, a binary quadratic form is a quadratic form in two variables. More concretely, it is a homogeneous polynomial of degree 2 in two variableswhere a, b, c are the coefficients...
s over the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. Since then, the concept has been generalized, and the connections with quadratic number fields, the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
, and other areas of mathematics have been further elucidated.
Real quadratic forms
Any n×n real symmetric matrix A determines a quadratic form qA in n variables by the formulaConversely, given a quadratic form in n variables, its coefficients can be arranged into an n×n symmetric matrix. One of the most important questions in the theory of quadratic forms is how much can one simplify a quadratic form q by a homogeneous linear change of variables. A fundamental theorem due to Jacobi asserts that q can be brought to a diagonal form
so that the corresponding symmetric matrix is diagonal
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
, and this is even possible to accomplish with a change of variables given by an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
– in this case the coefficients λ1, λ2, …, λn are in fact determined uniquely up to a permutation. If the change of variables is given by an invertible matrix, not necessarily orthogonal, then the coefficients λi can be made to be 0,1, and −1. Sylvester's law of inertia
Sylvester's law of inertia
Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of coordinates...
states that the numbers of 1 and −1 are invariants
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
of the quadratic form, in the sense that any other diagonalization will contain them in the same quantities. The signature of the quadratic form is the triple (n0, n+, n−) where n0 is the number 0s and n± is the number of ±1s. Sylvester's law of inertia shows that this is a well-defined quantity attached to the quadratic form. The case when all λi have the same sign is especially important: in this case the quadratic form is called positive definite (all 1) or negative definite (all −1); if none of the terms are 0 then the form is called ; this includes positive definite, negative definite, and indefinite (a mix of 1 and −1); equivalently, a nondegenerate quadratic form is one whose associated symmetric form is a nondegenerate bilinear form. A real vector space with an indefinite nondegenerate quadratic form of index
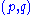 (p 1s, q −1s) is often denoted as
(p 1s, q −1s) is often denoted as 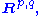 particularly in the physical theory of space-time.
particularly in the physical theory of space-time.Below we reformulate these results in a different way.
Let q be a quadratic form defined on an n-dimensional real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space. Let A be the matrix of the quadratic form q in a given basis. This means that A is a symmetric n×n matrix such that
where x is the column vector of coordinates of v in the chosen basis. Under a change of basis, the column x is multiplied on the left by an n×n invertible matrix S, and the symmetric square matrix A is transformed into another symmetric square matrix B of the same size according to the formula
Any symmetric matrix A can be transformed into a diagonal matrix
-

by a suitable choice of an orthogonal matrix S, and the diagonal entries of B are uniquely determined — this is Jacobi's theorem. If S is allowed to be any invertible matrix then B can be made to have only 0,1, and −1 on the diagonal, and the number of the entries of each type (n0 for 0, n+ for 1, and n− for −1) depends only on A. This is one of the formulations of Sylvester's law of inertia and the numbers n+ and n− are called the positive and negative indices of inertia. Although their definition involved a choice of basis and consideration of the corresponding real symmetric matrix A, Sylvester's law of inertia means that they are invariants of the quadratic form q.
The quadratic form q is positive definite (resp., negative definite) if q(v)>0 (resp., q(v)<0) for every nonzero vector v. When q(v) assumes both positive and negative values, q is an indefinite quadratic form. The theorems of Jacobi and Sylvester show that any positive definite quadratic form in n variables can be brought to the sum of n squares by a suitable invertible linear transformation: geometrically, there is only one positive definite real quadratic form of every dimension. Its isometry groupIsometry groupIn mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
is a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n). This stands in contrast with the case of indefinite forms, when the corresponding group, the indefinite orthogonal group O(p,q), is non-compact. Further, the isometry groups of Q and −Q are the same ( ), but the associated Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
), but the associated Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s (and hence Pin groupPin groupIn mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
s) are different.
Definitions
An n-ary quadratic form over a field K is a homogeneous polynomialHomogeneous polynomialIn mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree 2 in n variables with coefficients in K:
This formula may be rewritten using matrices: let x be the column vector with components x1, …, xn and A = (aij) be the n×n matrix over K whose entries are the coefficients of q. Then
Two n-ary quadratic forms φ and ψ over K are equivalent if there exists a nonsingular linear transformation T ∈GLn(K) such that
Let us assume that the characteristic of K is different from 2.
(The theory of quadratic forms over a field of characteristic 2 has important differences and many definitions and theorems have to be modified.) The coefficient matrix A of q may be replaced by the symmetric matrix 1/2(A + AT) with the same quadratic form, so it may be assumed from the outset that A is symmetric. Moreover, a symmetric matrix A is uniquely determined by the corresponding quadratic form. Under an equivalence T, the symmetric matrix A of φ and the symmetric matrix B of ψ are related as follows:
The associated bilinear form of a quadratic form q is defined by
Thus, bq is a symmetric bilinear formSymmetric bilinear formA symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
over K with matrix A. Conversely, any symmetric bilinear form b defines a quadratic form
and these two processes are the inverses of one another. As a consequence, over a field of characteristic not equal to 2, the theories of symmetric bilinear forms and of quadratic forms in n variables are essentially the same.
Quadratic spaces
A quadratic form q in n variables over K induces a map from the n-dimensional coordinate space Kn into K:
The map Q is a quadratic map, which means that it has the properties:
- The map BQ: V×V → K defined below is bilinear over K:
The pair (V,Q) consisting of a finite-dimensional vector space V over K and a quadratic map from V to K is called a quadratic space and BQ is the associated bilinear form of Q. The notion of a quadratic space is a coordinate-free version of the notion of quadratic form. Sometimes, Q is also called a quadratic form.
Two n-dimensional quadratic spaces (V,Q) and (V ′, Q ′) are isometric if there exists an invertible linear transformation T: V →V ′ (isometry) such that
The isometry classes of n-dimensional quadratic spaces over K correspond to the equivalence classes of n-ary quadratic forms over K.
Further definitions
Two elements v and w of V are called orthogonal if B(v, w)=0. The kernel of a bilinear form B consists of the elements that are orthogonal to each elements of V. Q is non-singular if the kernel of its associated bilinear form is 0. If there exists a non-zero v in V such that Q(v) = 0, the quadratic form Q is isotropicIsotropic quadratic formIn mathematics, a quadratic form over a field F is said to be isotropic if there is a non-zero vector on which it evaluates to zero. Otherwise the quadratic form is anisotropic. More precisely, if q is a quadratic form on a vector space V over F, then a non-zero vector v in V is said to be...
, otherwise it is anisotropic. This terminology also applies to vectors and subspaces of a quadratic space. If the restriction of Q to a subspace U of V is identically zero, U is totally singular.
The orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
of a non-singular quadratic form Q is the group of the linear automorphisms of V that preserve Q, i.e. the group of isometries of (V, Q) into itself.
Equivalence of forms
Every quadratic form q in n variables over a field of characteristic not equal to 2 is equivalent to a diagonal form
Such a diagonal form is often denoted by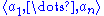 .
.
Classification of all quadratic forms up to equivalence can thus be reduced to the case of diagonal forms.
Geometric Meaning
If we let the equation be with symmetric matrix A, then the geometric meaning is as follows.
with symmetric matrix A, then the geometric meaning is as follows.
If all eigenvalues of A are non-zero, then it is an ellipsoid or a hyperboloid. If all the eigenvalues are positive, then it is an ellipsoid; if all the eigenvalues are negative, it is an image ellipsoid; if some eigenvalues are positive and some are negative, then it is a hyperboloid.
If there exist one or more eigenvalues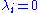 , then if the corresponding
, then if the corresponding  , it is a paraboloidParaboloidIn mathematics, a paraboloid is a quadric surface of special kind. There are two kinds of paraboloids: elliptic and hyperbolic. The elliptic paraboloid is shaped like an oval cup and can have a maximum or minimum point....
, it is a paraboloidParaboloidIn mathematics, a paraboloid is a quadric surface of special kind. There are two kinds of paraboloids: elliptic and hyperbolic. The elliptic paraboloid is shaped like an oval cup and can have a maximum or minimum point....
(either elliptic or hyperbolic); if the corresponding , the dimension i degenerates and does not get into play, and the geometric meaning will be determined by other eigenvalues and other components of b. When it is a paraboloid, whether it is elliptic or hyperbolic is determined by whether all other non-zero eigenvalues are of the same sign: if they are, then it is elliptic; otherwise, it is hyperbolic.
, the dimension i degenerates and does not get into play, and the geometric meaning will be determined by other eigenvalues and other components of b. When it is a paraboloid, whether it is elliptic or hyperbolic is determined by whether all other non-zero eigenvalues are of the same sign: if they are, then it is elliptic; otherwise, it is hyperbolic.
Integral quadratic forms
Quadratic forms over the ring of integers are called integral quadratic forms, whereas the corresponding modules are quadratic lattices (sometimes, simply latticeLattice (group)In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
s). They play an important role in number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
An integral quadratic form has integer coefficients, such as ; equivalently, given a lattice
; equivalently, given a lattice 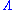 in a vector space
in a vector space  (over a field with characteristic 0, such as
(over a field with characteristic 0, such as  or
or  ), a quadratic form
), a quadratic form  is integral with respect to
is integral with respect to  if and only if it is integer-valued on
if and only if it is integer-valued on  , meaning
, meaning 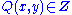 if
if  .
.
This is the current use of the term; in the past it was sometimes used differently, as detailed below.
Historical use
Historically there was some confusion and controversy over whether the notion of integral quadratic form should mean:
twos in: the quadratic form associated to a symmetric matrix with integer coefficients
twos out: a polynomial with integer coefficients (so the associated symmetric matrix may have half-integer coefficients off the diagonal)
This debate was due to the confusion of quadratic forms (represented by polynomials) and symmetric bilinear forms (represented by matrices), and "twos out" is now the accepted convention; "twos in" is instead the theory of integral symmetric bilinear forms (integral symmetric matrices).
In "twos in", binary quadratic forms are of the form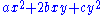 , represented by the symmetric matrix
, represented by the symmetric matrix 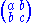 ; this is the convention GaussGaussGauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
; this is the convention GaussGaussGauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
uses in Disquisitiones ArithmeticaeDisquisitiones ArithmeticaeThe Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
.
In "twos out", binary quadratic forms are of the form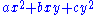 , represented by the symmetric matrix
, represented by the symmetric matrix  .
.
Several points of view mean that twos out has been adopted as the standard convention. Those include:- better understanding of the 2-adic theory of quadratic forms, the 'local' source of the difficulty;
- the latticeLattice (group)In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
point of view, which was generally adopted by the experts in the arithmetic of quadratic forms during the 1950s; - the actual needs for integral quadratic form theory in topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
for intersection theoryIntersection theoryIn mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
; - the Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
aspects.
Universal quadratic forms
A quadratic form representing all of the positive integers is sometimes called universal. Lagrange's four-square theoremLagrange's four-square theoremLagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
shows that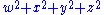 is universal. Ramanujan generalized this to
is universal. Ramanujan generalized this to 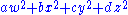 and found 54 {a,b,c,d} such that it can generate all positive integers, namely,
and found 54 {a,b,c,d} such that it can generate all positive integers, namely,
- {1,1,1,d}; d = 1-7
- {1,1,2,d}; d = 2-14
- {1,1,3,d}; d = 3-6
- {1,2,2,d}; d = 2-7
- {1,2,3,d}; d = 3-10
- {1,2,4,d}; d = 4-14
- {1,2,5,d}; d = 6-10
There are also forms that can express nearly all positive integers except one, such as {1,2,5,5} which has 15 as the exception. Recently, the 15 and 290 theorems have completely characterized universal integral quadratic forms: if all coefficients are integers, then it represents all positive integers if and only if it represents all integers up through 290; if it has an integral matrix, it represents all positive integers if and only if it represents all integers up through 15.
See also
- ε-quadratic form
- Quadratic form (statistics)Quadratic form (statistics)If \epsilon is a vector of n random variables, and \Lambda is an n-dimensional symmetric matrix, then the scalar quantity\epsilon^T\Lambda\epsilonis known as a quadratic form in \epsilon.-Expectation:It can be shown that...
- Discriminant#Discriminant of a quadratic form
- Cubic formCubic formIn mathematics, a cubic form is a homogeneous polynomial of degree 3, and a cubic hypersurface is the zero set of a cubic form.In , Boris Delone and Dmitriĭ Faddeev showed that binary cubic forms with integer coefficients can be used to parametrize orders in cubic fields...
- Witt groupWitt groupIn mathematics, a Witt group of a field, named after Ernst Witt, is an abelian group whose elements are represented by symmetric bilinear forms over the field.-Definition:Fix a field k. All vector spaces will be assumed to be finite-dimensional...
- Witt's theoremWitt's theoremWitt theorem, named after Ernst Witt, is a basic result in the algebraic theory of quadratic forms: any isometry between two subspaces of a nonsingular quadratic space over a field k may be extended to an isometry of the whole space. An analogous statement holds also for skew-symmetric, Hermitian...
- Hasse–Minkowski theoremHasse–Minkowski theoremThe Hasse–Minkowski theorem is a fundamental result in number theory which states that two quadratic forms over a number field are equivalent if and only if they are equivalent locally at all places, i.e. equivalent over every completion of the field...
- Orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
-