Orthogonal matrix
Encyclopedia
In linear algebra
, an orthogonal matrix (less commonly called orthonormal matrix), is a square matrix with real
entries whose columns and rows are orthogonal unit vectors (i.e., orthonormal
vectors).
Equivalently, a matrix Q is orthogonal if its transpose
is equal to its inverse: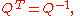
which entails
where I is the identity matrix
.
An orthogonal matrix Q is necessarily square, invertible (with inverse ), unitary , and normal
. As a linear transformation
, an orthogonal matrix preserves the dot product
of vectors, and therefore acts as an isometry
of Euclidean space
, such as a rotation
or reflection
. In other words, it is a unitary transformation
.
The set of n × n orthogonal matrices forms a group
O(n), known as the orthogonal group
. The subgroup
SO(n) consisting of orthogonal matrices with determinant
+1 is called the special orthogonal group, and each of its elements is a special orthogonal matrix. As a linear transformation, every special orthogonal matrix acts as a rotation.
The complex
analogue of an orthogonal matrix is a unitary matrix.
. Although we consider only real matrices here, the definition can be used for matrices with entries from any field
. However, orthogonal matrices arise naturally from dot products
, and for matrices of complex numbers that leads instead to the unitary requirement. Orthogonal matrices preserve the dot product, so, for vectors u, v in an n-dimensional real Euclidean space
To see the inner product connection, consider a vector v in an n-dimensional real Euclidean space
. Written with respect to an orthonormal basis, the squared length of v is vTv. If a linear transformation, in matrix form Qv, preserves vector lengths, then
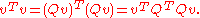
Thus finite-dimensional
linear isometries
—rotations, reflections, and their combinations—produce orthogonal matrices. The converse is also true: orthogonal matrices imply orthogonal transformations. However, linear algebra
includes orthogonal transformations between spaces which may be neither finite-dimensional nor of the same dimension, and these have no orthogonal matrix equivalent.
Orthogonal matrices are important for a number of reasons, both theoretical and practical. The n×n orthogonal matrices form a group
, the orthogonal group
denoted by O(n), which—with its subgroups—is widely used in mathematics and the physical sciences. For example, the point group
of a molecule is a subgroup of O(3). Because floating point versions of orthogonal matrices have advantageous properties, they are key to many algorithms in numerical linear algebra
, such as QR decomposition
. As another example, with appropriate normalization the discrete cosine transform
(used in MP3
compression) is represented by an orthogonal matrix.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, an orthogonal matrix (less commonly called orthonormal matrix), is a square matrix with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
entries whose columns and rows are orthogonal unit vectors (i.e., orthonormal
Orthonormality
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal and both of unit length. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length...
vectors).
Equivalently, a matrix Q is orthogonal if its transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
is equal to its inverse:
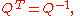
which entails
where I is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
An orthogonal matrix Q is necessarily square, invertible (with inverse ), unitary , and normal
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
. As a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
, an orthogonal matrix preserves the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of vectors, and therefore acts as an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, such as a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
or reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
. In other words, it is a unitary transformation
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
.
The set of n × n orthogonal matrices forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
O(n), known as the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
. The subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
SO(n) consisting of orthogonal matrices with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
+1 is called the special orthogonal group, and each of its elements is a special orthogonal matrix. As a linear transformation, every special orthogonal matrix acts as a rotation.
The complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
analogue of an orthogonal matrix is a unitary matrix.
Overview
An orthogonal matrix is the real specialization of a unitary matrix, and thus always a normal matrixNormal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
. Although we consider only real matrices here, the definition can be used for matrices with entries from any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. However, orthogonal matrices arise naturally from dot products
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, and for matrices of complex numbers that leads instead to the unitary requirement. Orthogonal matrices preserve the dot product, so, for vectors u, v in an n-dimensional real Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
To see the inner product connection, consider a vector v in an n-dimensional real Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Written with respect to an orthonormal basis, the squared length of v is vTv. If a linear transformation, in matrix form Qv, preserves vector lengths, then
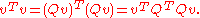
Thus finite-dimensional
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
linear isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
—rotations, reflections, and their combinations—produce orthogonal matrices. The converse is also true: orthogonal matrices imply orthogonal transformations. However, linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
includes orthogonal transformations between spaces which may be neither finite-dimensional nor of the same dimension, and these have no orthogonal matrix equivalent.
Orthogonal matrices are important for a number of reasons, both theoretical and practical. The n×n orthogonal matrices form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
denoted by O(n), which—with its subgroups—is widely used in mathematics and the physical sciences. For example, the point group
Point group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
of a molecule is a subgroup of O(3). Because floating point versions of orthogonal matrices have advantageous properties, they are key to many algorithms in numerical linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, such as QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
. As another example, with appropriate normalization the discrete cosine transform
Discrete cosine transform
A discrete cosine transform expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images A discrete cosine transform...
(used in MP3
MP3
MPEG-1 or MPEG-2 Audio Layer III, more commonly referred to as MP3, is a patented digital audio encoding format using a form of lossy data compression...
compression) is represented by an orthogonal matrix.
Examples
Below are a few examples of small orthogonal matrices and possible interpretations.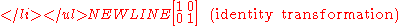
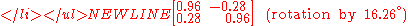
Lower dimensions
The simplest orthogonal matrices are the 1×1 matrices [1] and [−1] which we can interpret as the identity and a reflection of the real line across the origin.
The 2×2 matrices have the form
which orthogonality demands satisfy the three equations
-
In consideration of the first equation, without loss of generality let p = cos θ, q = sin θ; then either t = −q, u = p or t = q, u = −p. We can interpret the first case as a rotation by θ (where θ = 0 is the identity), and the second as a reflection across a line at an angle of θ/2.
The special case of the reflection matrix with θ=90° generates a reflection about the line 45° line y=x and therefore exchanges x and y; it is a permutation matrixPermutation matrixIn mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
, with a single 1 in each column and row (and otherwise 0):
The identity is also a permutation matrix.
A reflection is its own inverse, which implies that a reflection matrix is symmetric (equal to its transpose) as well as orthogonal. The product of two rotation matrices is a rotation matrix, and the product of two reflection matrices is also a rotation matrix.
Higher dimensions
Regardless of the dimension, it is always possible to classify orthogonal matrices as purely rotational or not, but for 3×3 matrices and larger the non-rotational matrices can be more complicated than reflections. For example,
represent an inversion through the origin and
a rotoinversionImproper rotationIn 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
about the z axis.
Rotations also become more complicated; they can no longer be completely characterized by an angle, and may affect more than one planar subspace. While it is common to describe a 3×3 rotation matrix in terms of an axis and angle, the existence of an axis is an accidental property of this dimension that applies in no other.
However, we have elementary building blocks for permutations, reflections, and rotations that apply in general.
Primitives
The most elementary permutation is a transposition, obtained from the identity matrix by exchanging two rows. Any n×n permutation matrix can be constructed as a product of no more than n − 1 transpositions.
A Householder reflection is constructed from a non-null vector v as
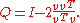
Here the numerator is a symmetric matrix while the denominator is a number, the squared magnitude of v. This is a reflection in the hyperplane perpendicular to v (negating any vector component parallel to v). If v is a unit vector, then Q = I − 2vvT suffices. A Householder reflection is typically used to simultaneously zero the lower part of a column. Any orthogonal matrix of size n×n can be constructed as a product of at most n such reflections.
A Givens rotation acts on a two-dimensional (planar) subspace spanned by two coordinate axes, rotating by a chosen angle. It is typically used to zero a single subdiagonal entry. Any rotation matrix of size n×n can be constructed as a product of at most n(n − 1)/2 such rotations. In the case of 3×3 matrices, three such rotations suffice; and by fixing the sequence we can thus describe all 3×3 rotation matrices (though not uniquely) in terms of the three angles used, often called Euler anglesEuler anglesThe Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
.
A Jacobi rotation has the same form as a Givens rotation, but is used as a similarity transformation chosen to zero both off-diagonal entries of a 2×2 symmetric submatrix.
Matrix properties
A real square matrix is orthogonal if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
its columns form an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of the Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn with the ordinary Euclidean dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, which is the case if and only if its rows form an orthonormal basis of Rn. It might be tempting to suppose a matrix with orthogonal (not orthonormal) columns would be called an orthogonal matrix, but such matrices have no special interest and no special name; they only satisfy MTM = D, with D a diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
.
The determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of any orthogonal matrix is +1 or −1. This follows from basic facts about determinants, as follows:
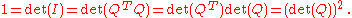
The converse is not true; having a determinant of +1 is no guarantee of orthogonality, even with orthogonal columns, as shown by the following counterexample.
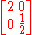
With permutation matrices the determinant matches the signatureEven and odd permutationsIn mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
, being +1 or −1 as the parity of the permutation is even or odd, for the determinant is an alternating function of the rows.
Stronger than the determinant restriction is the fact that an orthogonal matrix can always be diagonalizedDiagonalizable matrixIn linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
over the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s to exhibit a full set of eigenvalues, all of which must have (complex) modulusAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1.
Group properties
The inverse of every orthogonal matrix is again orthogonal, as is the matrix product of two orthogonal matrices. In fact, the set of all n×n orthogonal matrices satisfies all the axioms of a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. It is a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of dimension n(n − 1)/2, called the orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
and denoted by O(n).
The orthogonal matrices whose determinant is +1 form a path-connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of O(n) of indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2, the special orthogonal group SO(n) of rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s. The quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
O(n)/SO(n) is isomorphic to O(1), with the projection map choosing [+1] or [−1] according to the determinant. Orthogonal matrices with determinant −1 do not include the identity, and so do not form a subgroup but only a cosetCosetIn mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
; it is also (separately) connected. Thus each orthogonal group falls into two pieces; and because the projection map splitsExact sequenceAn exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
, O(n) is a semidirect productSemidirect productIn mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of SO(n) by O(1). In practical terms, a comparable statement is that any orthogonal matrix can be produced by taking a rotation matrix and possibly negating one of its columns, as we saw with 2×2 matrices. If n is odd, then the semidirect product is in fact a direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
, and any orthogonal matrix can be produced by taking a rotation matrix and possibly negating all of its columns. This follows from the property of determinants that negating a column negates the determinant, and thus negating an odd (but not even) number of columns negates the determinant.
Now consider (n+1)×(n+1) orthogonal matrices with bottom right entry equal to 1. The remainder of the last column (and last row) must be zeros, and the product of any two such matrices has the same form. The rest of the matrix is an n×n orthogonal matrix; thus O(n) is a subgroup of O(n + 1) (and of all higher groups).
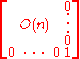
Since an elementary reflection in the form of a Householder matrix can reduce any orthogonal matrix to this constrained form, a series of such reflections can bring any orthogonal matrix to the identity; thus an orthogonal group is a reflection groupReflection groupIn group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
. The last column can be fixed to any unit vector, and each choice gives a different copy of O(n) in O(n+1); in this way O(n+1) is a bundleFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
over the unit sphere Sn with fiber O(n).
Similarly, SO(n) is a subgroup of SO(n+1); and any special orthogonal matrix can be generated by Givens plane rotations using an analogous procedure. The bundle structure persists: SO(n) ↪ SO(n+1) → Sn. A single rotation can produce a zero in the first row of the last column, and series of n−1 rotations will zero all but the last row of the last column of an n×n rotation matrix. Since the planes are fixed, each rotation has only one degree of freedom, its angle. By induction, SO(n) therefore has
degrees of freedom, and so does O(n).
Permutation matrices are simpler still; they form, not a Lie group, but only a finite group, the order n! symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn. By the same kind of argument, Sn is a subgroup of Sn+1. The even permutations produce the subgroup of permutation matrices of determinant +1, the order n!/2 alternating group.
Canonical form
More broadly, the effect of any orthogonal matrix separates into independent actions on orthogonal two-dimensional subspaces. That is, if Q is special orthogonal then one can always find an orthogonal matrix P, a (rotational) change of basis, that brings Q into block diagonal form:
where the matrices R1,...,Rk are 2×2 rotation matrices, and with the remaining entries zero. Exceptionally, a rotation block may be diagonal, ±I. Thus, negating one column if necessary, and noting that a 2×2 reflection diagonalizes to a +1 and −1, any orthogonal matrix can be brought to the form
The matrices R1,...,Rk give conjugate pairs of eigenvalues lying on the unit circle in the complex planeComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
; so this decomposition confirms that all eigenvalues have absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1. If n is odd, there is at least one real eigenvalue, +1 or −1; for a 3×3 rotation, the eigenvector associated with +1 is the rotation axis.
Lie algebra
Suppose the entries of Q are differentiable functions of t, and that t = 0 gives Q = I. Differentiating the orthogonality condition
yields
Evaluation at t = 0 (Q = I) then implies
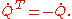
In Lie group terms, this means that the Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of an orthogonal matrix group consists of skew-symmetric matricesSkew-symmetric matrixIn mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
. Going the other direction, the matrix exponentialMatrix exponentialIn mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
of any skew-symmetric matrix is an orthogonal matrix (in fact, special orthogonal).
For example, the three-dimensional object physics calls angular velocityAngular velocityIn physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
is a differential rotation, thus a vector in the Lie algebra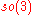
tangent to SO(3). Given ω = (xθ,yθ,zθ), with v = (x,y,z) a unit vector, the correct skew-symmetric matrix form of ω is
The exponential of this is the orthogonal matrix for rotation around axis v by angle θ; setting c = cos θ/2, s = sin θ/2,
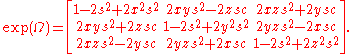
Benefits
Numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
takes advantage of many of the properties of orthogonal matrices for numerical linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, and they arise naturally. For example, it is often desirable to compute an orthonormal basis for a space, or an orthogonal change of bases; both take the form of orthogonal matrices. Having determinant ±1 and all eigenvalues of magnitude 1 is of great benefit for numeric stability. One implication is that the condition numberCondition numberIn the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
is 1 (which is the minimum), so errors are not magnified when multiplying with an orthogonal matrix. Many algorithms use orthogonal matrices like Householder reflections and Givens rotations for this reason. It is also helpful that, not only is an orthogonal matrix invertible, but its inverse is available essentially free, by exchanging indices.
Permutations are essential to the success of many algorithms, including the workhorse Gaussian eliminationGaussian eliminationIn linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
with partial pivoting (where permutations do the pivoting). However, they rarely appear explicitly as matrices; their special form allows more efficient representation, such as a list of n indices.
Likewise, algorithms using Householder and Givens matrices typically use specialized methods of multiplication and storage. For example, a Givens rotation affects only two rows of a matrix it multiplies, changing a full multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
of order n3 to a much more efficient order n. When uses of these reflections and rotations introduce zeros in a matrix, the space vacated is enough to store sufficient data to reproduce the transform, and to do so robustly. (Following , we do not store a rotation angle, which is both expensive and badly behaved.)
Decompositions
A number of important matrix decompositionMatrix decompositionIn the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
s involve orthogonal matrices, including especially:
-
- QR decompositionQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
:
- QR decomposition
-
- Singular value decompositionSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
: M = UΣVT, U and V orthogonal, Σ non-negative diagonal. - Eigendecomposition of a symmetric matrixEigendecomposition of a matrixIn the mathematical discipline of linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors...
(Decomposition according to Spectral theoremSpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
): S = QΛQT, S symmetric, Q orthogonal, Λ diagonal. - Polar decomposition: M = QS, Q orthogonal, S symmetric non-negative definite.
Examples
Consider an overdetermined system of linear equations, as might occur with repeated measurements of a physical phenomenon to compensate for experimental errors. Write Ax = b, where A is m×n, m > n.
A QR decomposition reduces A to upper triangular R. For example, if A is 5×3 then R has the form
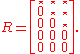
The linear least squaresLinear least squaresIn statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
problem is to find the x that minimizes ‖Ax − b‖, which is equivalent to projecting b to the subspace spanned by the columns of A. (Think of a pigeon flying over a parking lot with the sun straight overhead; its shadow hits the nearest point on the ground.) Assuming the columns of A (and hence R) are independent, the projection solution is found from ATAx = ATb. Now ATA is square (n×n) and invertible, and also equal to RTR. But the lower rows of zeros in R are superfluous in the product, which is thus already in lower-triangular upper-triangular factored form, as in Gaussian eliminationGaussian eliminationIn linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
(Cholesky decompositionCholesky decompositionIn linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
). Here orthogonality is important not only for reducing ATA = (RTQT)QR to RTR, but also for allowing solution without magnifying numerical problems.
In the case of a linear system which is underdetermined, or an otherwise non-invertible matrix, singular value decomposition (SVD) is equally useful. With A factored as UΣVT, a satisfactory solution uses the Moore-Penrose pseudoinversePseudoinverseIn mathematics, and in particular linear algebra, a pseudoinverse of a matrix is a generalization of the inverse matrix. The most widely known type of matrix pseudoinverse is the Moore–Penrose pseudoinverse, which was independently described by E. H. Moore in 1920, Arne Bjerhammar in 1951 and...
, VΣ+UT, where Σ+ merely replaces each non-zero diagonal entry with its reciprocal. Set x to VΣ+UTb.
The case of a square invertible matrix also holds interest. Suppose, for example, that A is a 3×3 rotation matrix which has been computed as the composition of numerous twists and turns. Floating point does not match the mathematical ideal of real numbers, so A has gradually lost its true orthogonality. A Gram-Schmidt process could orthogonalize the columns, but it is not the most reliable, nor the most efficient, nor the most invariant method. The polar decomposition factors a matrix into a pair, one of which is the unique closest orthogonal matrix to the given matrix, or one of the closest if the given matrix is singular. (Closeness can be measured by any matrix norm invariant under an orthogonal change of basis, such as the spectral norm or the Frobenius norm.) For a near-orthogonal matrix, rapid convergence to the orthogonal factor can be achieved by a "Newton's methodNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
" approach due to (1990), repeatedly averaging the matrix with its inverse transpose. has published an accelerated method with a convenient convergence test.
For example, consider a (very!) non-orthogonal matrix for which the simple averaging algorithm takes seven steps
and which acceleration trims to two steps (with γ = 0.353553, 0.565685).
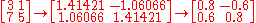
Gram-Schmidt yields an inferior solution, shown by a Frobenius distance of 8.28659 instead of the minimum 8.12404.
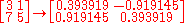
Randomization
Some numerical applications, such as Monte Carlo methodMonte Carlo methodMonte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
s and exploration of high-dimensional data spaces, require generation of uniformly distributedUniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
random orthogonal matrices. In this context, "uniform" is defined in terms of Haar measureHaar measureIn mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
, which essentially requires that the distribution not change if multiplied by any freely chosen orthogonal matrix. Orthogonalizing matrices with independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
uniformly distributed random entries does not result in uniformly distributed orthogonal matrices, but the QR decompositionQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
of independent normally distributed random entries does, as long as the diagonal of R contains only positive entries. replaced this with a more efficient idea that later generalized as the "subgroup algorithm" (in which form it works just as well for permutations and rotations). To generate an (n + 1)×(n + 1) orthogonal matrix, take an n×n one and a uniformly distributed unit vector of dimension n + 1. Construct a Householder reflection from the vector, then apply it to the smaller matrix (embedded in the larger size with a 1 in the bottom corner).
Nearest orthogonal matrix
The problem of finding the orthogonal matrix
nearest a given matrix 
is related to the Orthogonal Procrustes problemOrthogonal Procrustes problemThe orthogonal Procrustes problem is a matrix approximation problem in linear algebra. In its classical form, one is given two matrices A and B and asked to find an orthogonal matrix R which most closely maps A to B...
. There are several different ways to get the unique solution, the simplest of which is taking the singular value decompositionSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
of
and replacing the singular values with ones. Another method expresses the 
explicitly but requires the use of a matrix square root:
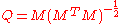
This may be combined with the Babylonian method for extracting the square root of a matrix to give a recurrence which converges to an orthogonal matrix quadratically:
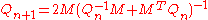
where
. These iterations are stable provided the condition numberCondition numberIn the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
of
is less than three.
Spin and Pin
A subtle technical problem afflicts some uses of orthogonal matrices. Not only are the group components with determinant +1 and −1 not connected to each other, even the +1 component, SO(n), is not simply connectedSimply connected spaceIn topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
(except for SO(1), which is trivial). Thus it is sometimes advantageous, or even necessary, to work with a covering groupCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
of SO(n), the spin group, Spin(n). Likewise, O(n) has covering groups, the pin groupPin groupIn mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
s, Pin(n). For n > 2, Spin(n) is simply connected, and thus the universal covering group for SO(n). By far the most famous example of a spin group is Spin(3), which is nothing but SU(2), or the group of unit quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s.
The Pin and Spin groups are found within Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s, which themselves can be built from orthogonal matrices.
Rectangular matrices
If Q is not a square matrix, then the conditions QTQ = I and QQT = I are not equivalent. The condition QTQ = I says that the columns of Q are orthonormal. This can only happen if Q is an m×n matrix with n ≤ m. Similarly, QQT = I says that the rows of Q are orthonormal, which requires n ≥ m.
There is no standard terminology for these matrices. They are sometimes called "orthonormal matrices", sometimes "orthogonal matrices", and sometimes simply "matrices with orthonormal rows/columns".
See also
- Orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
- Coordinate rotation
- Unitary matrix
- Symplectic matrix
- Skew-symmetric matrixSkew-symmetric matrixIn mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
, a matrix whose transpose is its negative
External links
-