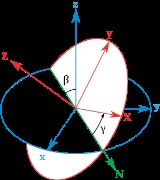
The Euler angles are three angles introduced by Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

 to describe the orientation

Orientation (geometry)

In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....

 of a rigid body

Rigid body

In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...

. To describe such an orientation in 3-dimensional

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

 Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 three parameters are required. They can be given in several ways, Euler angles being one of them; see charts on SO(3)

Charts on SO(3)

In mathematics, the special orthogonal group in three dimensions, otherwise known as the rotation group SO, is a naturally occurring example of a manifold. The various charts on SO set up rival coordinate systems: in this case there cannot be said to be a preferred set of parameters describing a...

 for others.

Euler angles also represent three composed rotations that move a reference frame to a given referred frame. This is equivalent to saying that any orientation can be achieved by composing three elemental rotation

Rotation

A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

s (rotations around a single axis), and also equivalent to saying that any rotation matrix can be decomposed

Matrix decomposition

In the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...

 as a product of three elemental rotation matrices.

Without considering the possibilities of different signs for the angles or moving the reference frame, there are twelve different conventions divided in two groups.