
Matrix decomposition
Encyclopedia
In the mathematical
discipline of linear algebra
, a matrix decomposition is a factorization
of a matrix into some canonical form
. There are many different matrix decompositions; each finds use among a particular class of problems.
, different decompositions are used to implement efficient matrix algorithm
s.
For instance, when solving a system of linear equations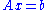 , the matrix A can be decomposed via the LU decomposition
, the matrix A can be decomposed via the LU decomposition
. The LU decomposition factorizes a matrix into a lower triangular matrix L and an upper triangular matrix U. The systems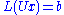 and
and 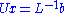 require fewer additions and multiplications to solve, compared with the original system
require fewer additions and multiplications to solve, compared with the original system 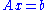 , though one might require significantly more digits in inexact arithmetic such as floating point
, though one might require significantly more digits in inexact arithmetic such as floating point
.
Similarly, the QR decomposition
expresses A as QR with Q a unitary matrix and R an upper triangular matrix. The system Q(Rx) = b is solved by Rx = QTb = c, and the system Rx = c is solved by 'back substitution'. The number of additions and multiplications required is about twice that of using the LU solver, but no more digits are required in inexact arithmetic because the QR decomposition is numerically stable.
LU decomposition
Cholesky decomposition
QR decomposition
Singular value decomposition
and the Jordan–Chevalley decomposition
Schur decomposition
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
discipline of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a matrix decomposition is a factorization
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
of a matrix into some canonical form
Canonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
. There are many different matrix decompositions; each finds use among a particular class of problems.
Example
In numerical analysisNumerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, different decompositions are used to implement efficient matrix algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s.
For instance, when solving a system of linear equations
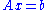 , the matrix A can be decomposed via the LU decomposition
, the matrix A can be decomposed via the LU decompositionLU decomposition
In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
. The LU decomposition factorizes a matrix into a lower triangular matrix L and an upper triangular matrix U. The systems
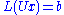 and
and 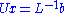 require fewer additions and multiplications to solve, compared with the original system
require fewer additions and multiplications to solve, compared with the original system 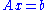 , though one might require significantly more digits in inexact arithmetic such as floating point
, though one might require significantly more digits in inexact arithmetic such as floating pointFloating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
.
Similarly, the QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
expresses A as QR with Q a unitary matrix and R an upper triangular matrix. The system Q(Rx) = b is solved by Rx = QTb = c, and the system Rx = c is solved by 'back substitution'. The number of additions and multiplications required is about twice that of using the LU solver, but no more digits are required in inexact arithmetic because the QR decomposition is numerically stable.
LU decompositionLU decompositionIn linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
- Applicable to: square matrix A
- Decomposition:
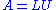 , where L is lower triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
, where L is lower triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
and U is upper triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero... - Related: the LDU decomposition is
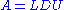 , where L is lower triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
, where L is lower triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
with ones on the diagonal, U is upper triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
with ones on the diagonal, and D is a diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. - Related: the LUP decomposition is
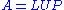 , where L is lower triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
, where L is lower triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
, U is upper triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
, and P is a permutation matrixPermutation matrixIn mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
. - Existence: An LUP decomposition exists for any square matrix A. When P is an identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, the LUP decomposition reduces to the LU decomposition. If the LU decomposition exists, the LDU decomposition does too. - Comments: The LUP and LU decompositions are useful in solving an n-by-n system of linear equations
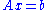 . These decompositions summarize the process of Gaussian eliminationGaussian eliminationIn linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
. These decompositions summarize the process of Gaussian eliminationGaussian eliminationIn linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
in matrix form. Matrix P represents any row interchanges carried out in the process of Gaussian elimination. If Gaussian elimination produces the row echelon formRow echelon formIn linear algebra a matrix is in row echelon form if* All nonzero rows are above any rows of all zeroes, and...
without requiring any row interchanges, then P=I, so an LU decomposition exists.
Cholesky decompositionCholesky decompositionIn linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
- Applicable to: square, symmetric, positive definitePositive-definite matrixIn linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
matrix A - Decomposition:
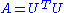 , where U is upper triangular with positive diagonal entries
, where U is upper triangular with positive diagonal entries - Comment: the Cholesky decomposition is a special case of the symmetric LU decomposition, with
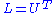 .
. - Comment: the Cholesky decomposition is unique
- Comment: the Cholesky decomposition is also applicable for complex hermitian positive definite matrices
- Comment: An alternative is the LDL decomposition which can avoid extracting square roots.
QR decompositionQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
- Applicable to: m-by-n matrix A
- Decomposition:
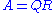 where Q is an orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
where Q is an orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
of size m-by-m, and R is an upper triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
matrix of size m-by-n - Comment: The QR decomposition provides an alternative way of solving the system of equations
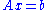 without inverting the matrix A. The fact that Q is orthogonalOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
without inverting the matrix A. The fact that Q is orthogonalOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
means that , so that
, so that 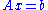 is equivalent to
is equivalent to 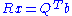 , which is easier to solve since R is triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
, which is easier to solve since R is triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
.
Singular value decompositionSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
- Applicable to: m-by-n matrix A.
- Decomposition:
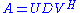 , where D is a nonnegative diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
, where D is a nonnegative diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
, and U and V are unitary matrices, and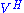 denotes the conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
denotes the conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of V (or simply the transpose, if V contains real numbers only). - Comment: The diagonal elements of D are called the singular values of A.
- Comment: like the eigendecomposition below, the singular value decomposition involves finding basis directions along which matrix multiplication is equivalent to scalar multiplication, but it has greater generality since the matrix under consideration need not be square.
Eigendecomposition
- Also called spectral decomposition
- Applicable to: square matrix A.
- Decomposition:
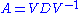 , where D is a diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
, where D is a diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
formed from the eigenvalues of A, and the columns of V are the corresponding eigenvectors of A. - Existence: An n-by-n matrix A always has n eigenvalues, which can be ordered (in more than one way) to form an n-by-n diagonal matrix D and a corresponding matrix of nonzero columns V that satisfies the eigenvalue equation
 . If the n eigenvalues are distinct (that is, none is equal to any of the others), then V is invertible, implying the decomposition
. If the n eigenvalues are distinct (that is, none is equal to any of the others), then V is invertible, implying the decomposition 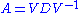 .
. - Comment: The eigendecomposition is useful for understanding the solution of a system of linear ordinary differential equations or linear difference equations. For example, the difference equation
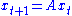 starting from the initial condition
starting from the initial condition 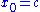 is solved by
is solved by 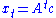 , which is equivalent to
, which is equivalent to 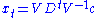 , where V and D are the matrices formed from the eigenvectors and eigenvalues of A. Since D is diagonal, raising it to power
, where V and D are the matrices formed from the eigenvectors and eigenvalues of A. Since D is diagonal, raising it to power 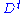 , just involves raising each element on the diagonal to the power t. This is much easier to do and to understand than raising A to power t, since A is usually not diagonal.
, just involves raising each element on the diagonal to the power t. This is much easier to do and to understand than raising A to power t, since A is usually not diagonal.
Jordan decomposition
The Jordan normal formJordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
and the Jordan–Chevalley decomposition
- Applicable to: square matrix A
- Comment: the Jordan normal form generalizes the eigendecomposition to cases where there are repeated eigenvalues and cannot be diagonalized, the Jordan–Chevalley decomposition does this without choosing a basis.
Schur decompositionSchur decompositionIn the mathematical discipline of linear algebra, the Schur decomposition or Schur triangulation, named after Issai Schur, is a matrix decomposition.- Statement :...
- Applicable to: square matrix A
- Comment: there are two versions of this decomposition: the complex Schur decomposition and the real Schur decomposition. A complex matrix always has a complex Schur decomposition. A real matrix admits a real Schur decomposition if and only if all of its eigenvalues are real.
- Decomposition (complex version):
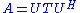 , where U is a unitary matrix,
, where U is a unitary matrix, 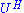 is the conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
is the conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of U, and T is an upper triangular matrix called the complex Schur form which has the eigenvalues of A along its diagonal. - Decomposition (real version):
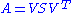 , where A, V, S and
, where A, V, S and 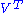 are matrices that contain real numbers only. In this case, V is an orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
are matrices that contain real numbers only. In this case, V is an orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
,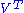 is the transpose of V, and S is a block upper triangularBlock matrixIn the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
is the transpose of V, and S is a block upper triangularBlock matrixIn the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
matrix called the real Schur form. The blocks on the diagonal of S are of size 1×1 (in which case they represent real eigenvalues) or 2×2 (in which case they are derived from complex conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
eigenvalue pairs).
QZ decomposition
- Also called: generalized Schur decomposition
- Applicable to: square matrices A and B
- Comment: there are two versions of this decomposition: complex and real.
- Decomposition (complex version):
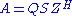 and
and  where Q and Z are unitary matrices, the H superscript represents conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
where Q and Z are unitary matrices, the H superscript represents conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
, and S and T are upper triangular matrices. - Comment: in the complex QZ decomposition, the ratios of the diagonal elements of S to the corresponding diagonal elements of T,
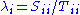 , are the generalized eigenvalues that solve the generalized eigenvalue problem
, are the generalized eigenvalues that solve the generalized eigenvalue problem 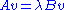 (where
(where 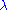 is an unknown scalar and v is an unknown nonzero vector).
is an unknown scalar and v is an unknown nonzero vector). - Decomposition (real version):
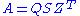 and
and 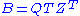 where A, B, Q, Z, S, and T are matrices containing real numbers only. In this case Q and Z are orthogonal matricesOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
where A, B, Q, Z, S, and T are matrices containing real numbers only. In this case Q and Z are orthogonal matricesOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
, the T superscript represents transposition, and S and T are block upper triangularBlock matrixIn the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
matrices. The blocks on the diagonal of S and T are of size 1×1 or 2×2.
Takagi's factorization
- Applicable to: square, complex, symmetric matrix A.
- Decomposition:
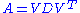 , where D is a real nonnegative diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
, where D is a real nonnegative diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
, and V is unitary.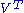 denotes the matrix transpose of V.
denotes the matrix transpose of V. - Comment: the diagonal elements of D are the nonnegative square roots of the eigenvalues of
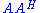 .
. - Comment: V may be complex even if A is real.
External links
- Online Matrix Calculator
- Springer Encyclopaedia of Mathematics » Matrix factorization
- GraphLab GraphLab collaborative filtering library, large scale parallel implementation of matrix decomposition methods (in C++) for multicore.

