
Row echelon form
Encyclopedia
In linear algebra
a matrix
is in row echelon form if
This is an example of 3x4 matrix in row echelon form:

A matrix is in reduced row echelon form (also called row canonical form) if it satisfies the additional condition:
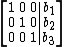
Note that this does not always mean that the left of the matrix will be an identity matrix. For example, the following matrix is also in reduced row-echelon form:
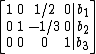
because the constants in the third column do not lead any rows.
, any matrix can be transformed to row echelon form. Since elementary row operations preserve the row space
of the matrix, the row space of the row echelon form is the same as that of the original matrix.
The resulting echelon form is not unique; for example, any multiple of a matrix in echelon form is also in echelon form. However, it has been proven that any matrix can be transformed to exactly one matrix in reduced row echelon form. This means that the nonzero rows of the reduced row echelon form are the unique reduced row echelon generating set for the row space of the original matrix.
is in row echelon form. Similarly, a system of equations is said to be in reduced row echelon form or canonical form if its augmented matrix is in reduced row echelon form.
converts a matrix to (non-reduced) row-echelon form:
function ToRowEchelonForm(Matrix M) is
nr := number of rows in M
nc := number of columns in M
for 0 ≤ r < nr do
allZeros := true
for 0 ≤ c < nc do
if M[r, c] != 0 then
allZeros := false
exit for
end if
end for
if allZeros = true then
In M, swap row r with row nr - 1
nr := nr - 1
end if
end for
p := 0
while p < nr and p < nc do
label nextPivot:
r := 1
while M[p, p] = 0 do
if (p + r) <= nr then
p := p + 1
goto nextPivot
end if
In M, swap row p with row (p + r) <-- bug. nr < p+r at this point
r := r + 1
end while
for 1 ≤ r < (nr - p) do
if M[p + r, p] != 0 then
x := -M[p + r, p] / M[p, p]
for p ≤ c < nc do
M[p + r, c] := M[p , c] * x + M[p + r, c]
end for
end if
end for
p := p + 1
end while
end function
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is in row echelon form if
- All nonzero rows (rows with at least one nonzero element) are above any rows of all zeroes, and
- The leading coefficient (the first nonzero number from the left, also called the pivotPivot elementThe pivot or pivot element is the element of a matrix, an array, or some other kind of finite set, which is selected first by an algorithm , to do certain calculations...
) of a nonzero row is always strictly to the right of the leading coefficient of the row above it.
This is an example of 3x4 matrix in row echelon form:

A matrix is in reduced row echelon form (also called row canonical form) if it satisfies the additional condition:
- Every leading coefficient is 1 and is the only nonzero entry in its column, like in this example:
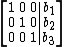
Note that this does not always mean that the left of the matrix will be an identity matrix. For example, the following matrix is also in reduced row-echelon form:
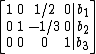
because the constants in the third column do not lead any rows.
Transformation to row echelon form
By means of a finite sequence of elementary row operationsElementary row operations
In mathematics, an elementary matrix is a simple matrix which differs from the identity matrix by one single elementary row operation. The elementary matrices generate the general linear group of invertible matrices...
, any matrix can be transformed to row echelon form. Since elementary row operations preserve the row space
Row space
In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...
of the matrix, the row space of the row echelon form is the same as that of the original matrix.
The resulting echelon form is not unique; for example, any multiple of a matrix in echelon form is also in echelon form. However, it has been proven that any matrix can be transformed to exactly one matrix in reduced row echelon form. This means that the nonzero rows of the reduced row echelon form are the unique reduced row echelon generating set for the row space of the original matrix.
Systems of linear equations
A system of linear equations is said to be in row echelon form if its augmented matrixAugmented matrix
In linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices.Given the matrices A and B, where:A =...
is in row echelon form. Similarly, a system of equations is said to be in reduced row echelon form or canonical form if its augmented matrix is in reduced row echelon form.
Pseudocode
The following pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
converts a matrix to (non-reduced) row-echelon form:
function ToRowEchelonForm(Matrix M) is
nr := number of rows in M
nc := number of columns in M
for 0 ≤ r < nr do
allZeros := true
for 0 ≤ c < nc do
if M[r, c] != 0 then
allZeros := false
exit for
end if
end for
if allZeros = true then
In M, swap row r with row nr - 1
nr := nr - 1
end if
end for
p := 0
while p < nr and p < nc do
label nextPivot:
r := 1
while M[p, p] = 0 do
if (p + r) <= nr then
p := p + 1
goto nextPivot
end if
In M, swap row p with row (p + r) <-- bug. nr < p+r at this point
r := r + 1
end while
for 1 ≤ r < (nr - p) do
if M[p + r, p] != 0 then
x := -M[p + r, p] / M[p, p]
for p ≤ c < nc do
M[p + r, c] := M[p , c] * x + M[p + r, c]
end for
end if
end for
p := p + 1
end while
end function

