Row space - AbsoluteAstronomy.com

Linear algebra

Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

, the row space of a matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

is the set of all possible linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

s of its row vectors. The row space of an m × n matrix is a subspace

Euclidean subspace

In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...

of n-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

. The dimension of the row space is called the row rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...

of the matrix.

Definition

Let A be an m × n matrix, with row vectors r₁, r₂, ..., r_m. A linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

of these vectors is any vector of the form

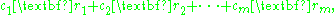
where c₁, c₂, ..., c_m are constants. The set of all possible linear combinations of r₁,...,r_m is called the row space of A. That is, the row space of A is the span

Linear span

In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...

of the vectors r₁,...,r_m.

For example, if

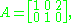
then the row vectors are r₁ = (1, 0, 2) and r₂ = (0, 1, 0). A linear combination of r₁ and r₂ is any vector of the form

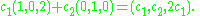
The set of all such vectors is the row space of A. In this case, the row space is precisely the set of vectors (x, y, z) ∈ R³ satisfying the equation z = 2x (using Cartesian coordinates, this set is a plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

through the origin in three-dimensional space

Three-dimensional space

Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...

).

For a matrix that represents a homogeneous system of linear equations, the row space consists of all linear equations that follow from those in the system.

The column space of

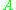is equal to the row space of

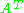Basis

The row space is not affected by elementary row operations

Elementary row operations

In mathematics, an elementary matrix is a simple matrix which differs from the identity matrix by one single elementary row operation. The elementary matrices generate the general linear group of invertible matrices...

. This makes it possible to use row reduction to find a basis

Basis (linear algebra)

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

for the row space.

For example, consider the matrix

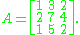
The rows of this matrix span the row space, but they may not be linearly independent, in which case the rows will not be a basis. To find a basis, we reduce A to row echelon form

Row echelon form

In linear algebra a matrix is in row echelon form if* All nonzero rows are above any rows of all zeroes, and...

:

r₁, r₂, r₃ represents the rows.

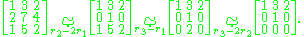
Once the matrix is in echelon form, the nonzero rows are a basis for the row space. In this case, the basis is { (1, 3, 2), (0, 1, 0) }. Another possible basis { (1, 0, 2), (0, 1, 0) } comes from a further reduction.

This algorithm can be used in general to find a basis for the span of a set of vectors. If the matrix is further simplified to reduced row echelon form, then the resulting basis is uniquely determined by the row space.

Dimension

The dimension of the row space is called the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...

of the matrix. This is the same as the maximum number of linearly independent rows that can be chosen from the matrix. For example, the 3 × 3 matrix in the example above has rank two.

The rank of a matrix is also equal to the dimension of the column space

Column space

In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...

. The dimension of the null space

Null space

In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...

is called the nullity of the matrix, and is related to the rank by the following equation:

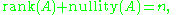
where n is the number of columns of the matrix A. The equation above is known as the rank-nullity theorem

Rank-nullity theorem

In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...

Relation to the null space

The null space

Null space

In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...

of matrix A is the set of all vectors x for which Ax = 0. The product of the matrix A and the vector x can be written in terms of the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

of vectors:
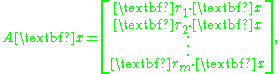
where r₁, ..., rm are the row vectors of A. Thus Ax = 0 if and only if x is orthogonal (perpendicular) to each of the row vectors of A.

It follows that the null space of A is the orthogonal complement to the row space. For example, if the row space is a plane through the origin in three dimensions, then the null space will be the perpendicular line through the origin. This provides a proof of the rank-nullity theorem

Rank-nullity theorem

(see dimension above).

The row space and null space are two of the four fundamental subspaces associated with a matrix A (the other two being the column space

Column space

and left null space).

Generalization to coimage

If V and W are vector spaces, then the kernel of a linear transformation

Linear transformation

In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...

T: V → W is the set of vectors v ∈ V for which T(v) = 0. The kernel of a linear transformation is analogous to the null space of a matrix.

If V is an inner product space

Inner product space

In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...

, then the orthogonal complement to the kernel can be thought of as a generalization of the row space. This is sometimes called the coimage

Coimage

In algebra, the coimage of a homomorphismis the quotientof domain and kernel.The coimage is canonically isomorphic to the image by the first isomorphism theorem, when that theorem applies....

of T. The transformation T is one-to-one on its coimage, and the coimage maps isomorphically

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...

onto the image

Image (mathematics)

In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...

of T.

When V is not an inner product space, the coimage of T can be defined as the quotient space

Quotient space (linear algebra)

In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....

V / ker(T).

External links

, MIT Linear Algebra Lecture on the Four Fundamental Subspaces at Google Video, from MIT OpenCourseWare

MIT OpenCourseWare

MIT OpenCourseWare is an initiative of the Massachusetts Institute of Technology to put all of the educational materials from its undergraduate- and graduate-level courses online, partly free and openly available to anyone, anywhere. MIT OpenCourseWare is a large-scale, web-based publication of...