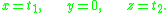In linear algebra

Linear algebra

Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

, a Euclidean subspace (or subspace of Rⁿ) is a set of vectors that is closed

Closure (mathematics)

In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...

 under addition and scalar multiplication. Geometrically, a subspace is a flat

Flat (geometry)

In geometry, a flat is a subset of n-dimensional space that is congruent to a Euclidean space of lower dimension. The flats in two-dimensional space are points and lines, and the flats in three-dimensional space are points, lines, and planes....

 in n-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 that passes through the origin. Examples of subspaces include the solution set to a homogeneous system of linear equations, the subset of Euclidean space described by a system of homogeneous linear parametric equations, the span

Linear span

In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...

 of a collection of vectors, and the null space

Null space

In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...

, column space

Column space

In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...

, and row space

Row space

In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...

 of a matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

.

In abstract linear algebra, Euclidean subspaces are important examples of vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

s. In this context, a Euclidean subspace is simply a linear subspace

Linear subspace

The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....

 of a Euclidean space.

Note on vectors and Rⁿ

In mathematics, Rⁿ denotes the set of all vectors with n real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 components:
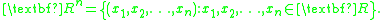
Here the word vector refers to any ordered list of numbers. Vectors can be written as either ordered tuples or as columns of numbers:
Geometrically, we regard vectors with n components as points in an n-dimensional space. That is, we identify the set Rⁿ with n-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

. Any subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

 of Rⁿ can be thought of as a geometric object (namely the object consisting of all the points in the subset). Using this mode of thought, a line in three-dimensional space is the same as the set of points on the line, and is therefore just a subset of R³.

Definition

A Euclidean subspace is a subset S of Rⁿ with the following properties:

1. The zero vector 0 is an element of S.
2. If u and v are elements of S, then is an element of S.
3. If v is an element of S and c is a scalar
   Scalar (mathematics)
   In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
   
   , then cv is an element of S.

There are several common variations on these requirements, all of which are logically equivalent

Logical equivalence

In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...

 to the list above.
Because subspaces are closed

Closure (mathematics)

In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...

 under both addition and scalar multiplication, any linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

 of vectors from a subspace is again in the subspace. That is, if

are elements of a subspace S, and

are scalars

Scalar (mathematics)

In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....

, then

c₁ v₁ + c₂ v₂ + · · · + c_k v_k

is again an element of S.
R2 is not a subspace of R3

Geometric description

Geometrically, a subspace of Rⁿ is simply a flat

Flat (geometry)

In geometry, a flat is a subset of n-dimensional space that is congruent to a Euclidean space of lower dimension. The flats in two-dimensional space are points and lines, and the flats in three-dimensional space are points, lines, and planes....

 through the origin, i.e. a copy of a lower dimensional (or equi-dimensional) Euclidean space sitting in n dimensions. For example, there are four different types of subspaces in R³:

1. The singleton set  is a zero-dimensional subspace of R³.
2. Any line
   Line (mathematics)
   The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
   
    through the origin is a one-dimensional subspace of R³.
3. Any plane
   Plane (mathematics)
   In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
   
    through the origin is a two-dimensional subspace of R³.
4. The entire set R³ is a three-dimensional subspace of itself.

In n-dimensional space, there are subspaces of every dimension from 0 to n.

The geometric dimension of a subspace is the same as the number of vectors required for a basis

Basis (linear algebra)

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

 (see below).

Systems of linear equations

The solution set to any homogeneous system of linear equations with n variables is a subspace of Rⁿ:


For example, the set of all vectors satisfying the equations


is a one-dimensional subspace of R³. More generally, that is to say that given a set of n, independent functions, the dimension of the subspace in R^k will be the dimension of the null set

Null set

In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...

 of A, the composite matrix of the n functions.

Null space of a matrix

In linear algebra, a homogeneous system of linear equations can be written as a single matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

 equation:


The set of solutions to this equation is known as the null space

Null space

In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...

 of the matrix. For example, the subspace of R³ described above is the null space of the matrix


Every subspace of Rⁿ can be described as the null space of some matrix (see algorithms, below).

Linear parametric equations

The subset of Rⁿ described by a system of homogeneous linear parametric equations is a subspace: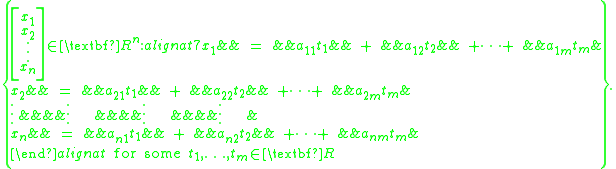


For example, the set of all vectors parameterized by the equations


is a two-dimensional subspace of R³.

Span of vectors

In linear algebra, the system of parametric equations can be written as a single vector equation:


The expression on the right is called a linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

 of the vectors
and . These two vectors are said to span the resulting subspace.

In general, a linear combination of vectors

is any vector of the form


The set of all possible linear combinations is called the span:


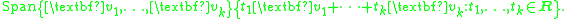
If the vectors v₁,...,v_k have n components, then their span is a subspace of Rⁿ. Geometrically, the span is the flat through the origin in n-dimensional space determined by the points v₁,...,v_k.

Example

The xz-plane in R³ can be parameterized by the equations

As a subspace, the xz-plane is spanned by the vectors and . Every vector in the xz-plane can be written as a linear combination of these two:

Geometrically, this corresponds to the fact that every point on the xz-plane can be reached from the origin by first moving some distance in the direction of and then moving some distance in the direction of .

Column space and row space

A system of linear parametric equations can also be written as a single matrix equation:


In this case, the subspace consists of all possible values of the vector x. In linear algebra, this subspace is known as the column space (or image

Image (mathematics)

In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...

) of the matrix A. It is precisely the subspace of Rⁿ spanned by the column vectors of A.

The row space of a matrix is the subspace spanned by its row vectors. The row space is interesting because it is the orthogonal complement of the null space (see below).

Independence, basis, and dimension

In general, a subspace of Rⁿ determined by k parameters (or spanned by k vectors) has dimension k. However, there are exceptions to this rule. For example, the subspace of R³ spanned by the three vectors , , and
is just the xz-plane, with each point on the plane described by infinitely many different values of .

In general, vectors v₁,...,v_k are called linearly independent if


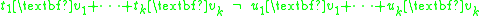
for
.
If are linearly independent, then the coordinates for a vector in the span are uniquely determined.

A basis for a subspace S is a set of linearly independent vectors whose span is S. The number of elements in a basis is always equal to the geometric dimension of the subspace. Any spanning set for a subspace can be changed into a basis by removing redundant vectors (see algorithms, below).

Example

Let S be the subspace of R⁴ defined by the equations

Then the vectors and are a basis for S. In particular, every vector that satisfies the above equations can be written uniquely as a linear combination of the two basis vectors:

The subspace S is two-dimensional. Geometrically, it is the plane in R⁴ passing through the points , , and .

Algorithms

Most algorithms for dealing with subspaces involve row reduction. This is the process of applying elementary row operations to a matrix until it reaches either row echelon form

Row echelon form

In linear algebra a matrix is in row echelon form if* All nonzero rows are above any rows of all zeroes, and...

 or reduced row echelon form. Row reduction has the following important properties:

1. The reduced matrix has the same null space as the original.
2. Row reduction does not change the span of the row vectors, i.e. the reduced matrix has the same row space as the original.
3. Row reduction does not affect the linear dependence of the column vectors.

Basis for a row space

Input An matrix A.

Output A basis for the row space

Row space

In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...

 of A.

1. Use elementary row operations to put A into row echelon form.
2. The nonzero rows of the echelon form are a basis for the row space of A.

See the article on row space

Row space

In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...

 for an example.

If we instead put the matrix A into reduced row echelon form, then the resulting basis for the row space is uniquely determined. This provides an algorithm for checking whether two row spaces are equal and, by extension, whether two subspaces of Rⁿ are equal.

Subspace membership

Input A basis {b₁, b₂, ..., b_k} for a subspace S of Rⁿ, and a vector v with n components.

Output Determines whether v is an element of S

1. Create a (k + 1) × n matrix A whose rows are the vectors b₁,...,b_k and v.
2. Use elementary row operations to put A into row echelon form.
3. If the echelon form has a row of zeroes, then the vectors are linearly dependent, and therefore .

Basis for a column space

Input An m × n matrix A

Output A basis for the column space

Column space

In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...

 of A

1. Use elementary row operations to put A into row echelon form.
2. Determine which columns of the echelon form have pivots
   Row echelon form
   In linear algebra a matrix is in row echelon form if* All nonzero rows are above any rows of all zeroes, and...
   
   . The corresponding columns of the original matrix are a basis for the column space.

See the article on column space

Column space

In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...

 for an example.

This produces a basis for the column space that is a subset of the original column vectors. It works because the columns with pivots are a basis for the column space of the echelon form, and row reduction does not change the linear dependence relationships between the columns.

Coordinates for a vector

Input A basis {b₁, b₂, ..., b_k} for a subspace S of Rⁿ, and a vector

Output Numbers t₁, t₂, ..., t_k such that

1. Create an augmented matrix
   Augmented matrix
   In linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices.Given the matrices A and B, where:A =...
   
    A whose columns are b₁,...,b_k , with the last column being v.
2. Use elementary row operations to put A into reduced row echelon form.
3. Express the final column of the reduced echelon form as a linear combination of the first k columns. The coefficients used are the desired numbers . (These should be precisely the first k entries in the final column of the reduced echelon form.)

If the final column of the reduced row echelon form contains a pivot, then the input vector v does not lie in S.

Basis for a null space

Input An m × n matrix A.

Output A basis for the null space of A

1. Use elementary row operations to put A in reduced row echelon form.
2. Using the reduced row echelon form, determine which of the variables are free. Write equations for the dependent variables in terms of the free variables.
3. For each free variable x_i, choose a vector in the null space for which and the remaining free variables are zero. The resulting collection of vectors is a basis for the null space of A.

See the article on null space

Null space

In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...

 for an example.

Equations for a subspace

Input A basis {b₁, b₂, ..., b_k} for a subspace S of Rⁿ

Output An (n − k) × n matrix whose null space is S.

1. Create a matrix A whose rows are .
2. Use elementary row operations to put A into reduced row echelon form.
3. Let be the columns of the reduced row echelon form. For each column without a pivot, write an equation expressing the column as a linear combination of the columns with pivots.
4. This results in a homogeneous system of n − k linear equations involving the variables c₁,...,c_n. The matrix corresponding to this system is the desired matrix with nullspace S.

Example

If the reduced row echelon form of A is

then the column vectors satisfy the equations

It follows that the row vectors of A satisfy the equations

In particular, the row vectors of A are a basis for the null space of the corresponding matrix.

Operations on subspaces

Intersection

If U and V are subspaces of Rⁿ, their intersection

Intersection (set theory)

In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....

 is also a subspace:


The dimension of the intersection satisfies the inequality


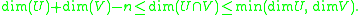
The minimum is the most common case, and the maximum only occurs when one subspace is contained in the other. For example, the intersection of two-dimensional subspaces in R³ has dimension one or two (with two only possible if they are the same plane). The intersection of three-dimensional subspaces in R⁵ has dimension one, two, or three, with most pairs intersecting along a line.

The codimension

Codimension

In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...

 of a subspace U in Rⁿ is the difference
. Using codimension, the inequality above can be written

Sum

If U and V are subspaces of Rⁿ, their sum is the subspace


For example, the sum of two lines is the plane that contains them both. The dimension of the sum satisfies the inequality


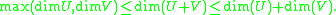
Here the minimum only occurs if one subspace is contained in the other, while the maximum is the most general case. The dimension of the intersection and the sum are related:

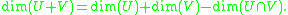
Orthogonal complement

The orthogonal complement of a subspace U is the subspace


Here x · u denotes the dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

 of x and u. For example, if U is a plane through the origin in R³, then U^⊥ is the line perpendicular to this plane at the origin.

If b₁, b₂, ..., b_k is a basis for U, then a vector x is in the orthogonal complement of U if and only if it is orthogonal to each b_i. It follows that the null space of a matrix is the orthogonal complement of the row space.

The dimension of a subspace and its orthogonal complement are related by the equation


That is, the dimension of U^⊥ is equal to the codimension

Codimension

In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...

 of U. The intersection of U and U^⊥ is the origin, and the sum of U and U^⊥ is all of Rⁿ

Orthogonal complements satisfy a version of De Morgan's laws:


In fact, the collection of subspaces of Rⁿ satisfy all of the axioms for a Boolean algebra, with intersection as AND, sum as OR, and orthogonal complement as NOT.

External links

, MIT Linear Algebra Lecture on the Four Fundamental Subspaces at Google Video, from MIT OpenCourseWare

MIT OpenCourseWare

MIT OpenCourseWare is an initiative of the Massachusetts Institute of Technology to put all of the educational materials from its undergraduate- and graduate-level courses online, partly free and openly available to anyone, anywhere. MIT OpenCourseWare is a large-scale, web-based publication of...

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.