Image (mathematics) - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, an image is the subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

of a function's codomain

Codomain

In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...

which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function. The inverse image or preimage of a particular subset S of the codomain

Codomain

In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...

of a function is the set of all elements of the domain that map to the members of S.

Image and inverse image may also be defined for general binary relations, not just functions.

Definition

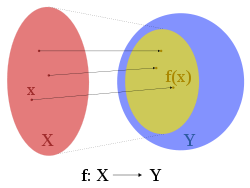
The word "image" is used in three related ways. In these definitions, f : X → Y is a function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

from the set X to the set Y.

Image of an element:
If x is a member of X, then f(x) = y (the value

Value (mathematics)

In mathematics, value commonly refers to the 'output' of a function. In the most basic case, that of unary, single-valued functions, there is one input and one output .The function f of the example is real-valued, since each and every possible function value is real...

of f when applied to x) is the image of x under f. y is alternatively known as the output of f for argument x.

Image of a subset
The image of a subset A ⊆ X under f is the subset f[A] ⊆ Y defined by (in set-builder notation

Set-builder notation

In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...

When there is no risk of confusion, f[A] is simply written as f(A). This convention is a common one; the intended meaning must be inferred from the context. This makes the image of f a function whose domain is the power set of X (the set of all subset

Subset

s of X), and whose codomain

Codomain

In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...

is the power set of Y. See Notation below.

Image of a function

The image f[X] of the entire domain X of f is called simply the image of f .

Inverse image

Let f be a function from X to Y. The preimage or inverse image of a set B ⊆ Y under f is the subset of X defined by

The inverse image of a singleton, denoted by f⁻¹[{y}] or by f⁻¹[y], is also called the fiber over y or the level set

Level set

In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....

of y. The set of all the fibers over the elements of Y is a family of sets indexed by Y.

Again, if there is no risk of confusion, we may denote f⁻¹[B] by f⁻¹(B), and think of f⁻¹ as a function from the power set of Y to the power set of X. The notation f⁻¹ should not be confused with that for inverse function

Inverse function

In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...

. The two coincide only if f is a bijection

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

Notation for image and inverse image

The traditional notations used in the previous section can be confusing. An alternative is to give explicit names for the image and preimage as functions between powersets:

Arrow notation

with
with .

Star notation

instead of .
instead of .

Other terminology

An alternative notation for f[A] used in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...

and set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

is f "A.
Some texts refer to the image of f as the range of f, but this usage should be avoided because the word "range" is also commonly used to mean the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...

of f.

Examples

1. f: {1,2,3} → {a,b,c,d} defined by

The image of the set {2,3} under f is f({2,3}) = {a,c}. The image of the function f is {a,c}. The preimage of a is f⁻¹({a}) = {1,2}. The preimage of {a,b} is also {1,2}. The preimage of {b,d} is the empty set

Empty set

In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...

{}.

2. f: R → R defined by f(x) = x².

The image of {-2,3} under f is f({-2,3}) = {4,9}, and the image of f is R⁺. The preimage of {4,9} under f is f⁻¹({4,9}) = {-3,-2,2,3}. The preimage of set N = {n ∈ R | n < 0} under f is the empty set, because the negative numbers do not have square roots in the set of reals.

3. f: R² → R defined by f(x, y) = x² + y².

The fibres f⁻¹({a}) are concentric circles about the origin

Origin (mathematics)

In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...

, the origin itself, and the empty set

Empty set

, depending on whether a>0, a=0, or a<0, respectively.

4. If M is a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

and π :TM→M is the canonical projection

Projection (mathematics)

Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...

from the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

TM to M, then the fibres of π are the tangent spaces T_x(M) for x∈M. This is also an example of a fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

Consequences

Given a function f : X → Y, for all subsets A, A₁, and A₂ of X and all subsets B, B₁, and B₂ of Y we have:

f(A₁ ∪ A₂) = f(A₁) ∪ f(A₂)
f(A₁ ∩ A₂) ⊆ f(A₁) ∩ f(A₂)
f⁻¹(B₁ ∪ B₂) = f⁻¹(B₁) ∪ f⁻¹(B₂)
f⁻¹(B₁ ∩ B₂) = f⁻¹(B₁) ∩ f⁻¹(B₂)
f(A) ⊆ B ⇔ A ⊆ f⁻¹(B)
f(f⁻¹(B)) ⊆ B
f⁻¹(f(A)) ⊇ A
A₁ ⊆ A₂ ⇒ f(A₁) ⊆ f(A₂)
B₁ ⊆ B₂ ⇒ f⁻¹(B₁) ⊆ f⁻¹(B₂)
f⁻¹(B^C) = (f⁻¹(B))^C
(f |_A)⁻¹(B) = A ∩ f⁻¹(B).

The results relating images and preimages to the (Boolean) algebra of intersection

Intersection (set theory)

In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....

and union

Union (set theory)

In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...

work for any collection of subsets, not just for pairs of subsets:

(Here, S can be infinite, even uncountably infinite.)

With respect to the algebra of subsets, by the above we see that the inverse image function is a lattice homomorphism while the image function is only a semilattice

Semilattice

In mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...

homomorphism (it does not always preserve intersections).

Definition

Inverse image

Notation for image and inverse image

Examples

Consequences

See also