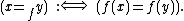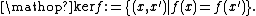Kernel of a function
Encyclopedia
In set theory
, the kernel of a function
f may be taken to be either
For the formal definition, let X and Y be sets and let f be a function from X to Y.
Elements x1 and x2 of X are equivalent if f(x1) and f(x2) are equal, i.e. are the same element of Y.
The kernel of f is the equivalence relation thus defined.
The kernel, in the equivalence-relation sense, may be denoted "=f" (or a variation) and may be defined symbolically as
to form a quotient set, and the quotient set is the partition:
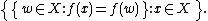
This quotient set X/=f is called the coimage
of the function f, and denoted "coim f" (or a variation).
The coimage is naturally isomorphic (in the set-theoretic sense of a bijection
) to the image
, im f; specifically, the equivalence class of x in X (which is an element of coim f) corresponds to f(x) in Y (which is an element of im f).
Like any binary relation
, the kernel of a function may be thought of as a subset
of the Cartesian product
X × X.
In this guise, the kernel may be denoted "ker f" (or a variation) and may be defined symbolically as
But this is not useful merely as a formalisation in set theory!
In fact, the study of the properties of this subset can shed important light on the function in question.
We give here two examples.
First, if X and Y are algebraic structure
s of some fixed type (such as group
s, rings, or vector space
s), and if the function f from X to Y is a homomorphism
, then ker f will be a subalgebra
of the direct product
X × X. Subalgebras of X × X that are also equivalence relations (called congruence relation
s) are important in abstract algebra
, because they define the most general notion of quotient algebra
. Thus the coimage of f is a quotient algebra of X much as the image of f is a subalgebra of Y; and the bijection between them becomes an isomorphism
in the algebraic sense as well (this is the most general form of the first isomorphism theorem in algebra). The use of kernels in this context is discussed further in the article Kernel (algebra)
.
Secondly, if X and Y are topological space
s and f is a continuous function
between them, then the topological properties of ker f can shed light on the spaces X and Y.
For example, if Y is a Hausdorff space
, then ker f must be a closed set
.
Conversely, if X is a Hausdorff space and ker f is a closed set, then the coimage of f, if given the quotient space topology, must also be a Hausdorff space.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, the kernel of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f may be taken to be either
- the equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the function's domain that roughly expresses the idea of "equivalent as far as the function f can tell", or - the corresponding partitionPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the domain.
For the formal definition, let X and Y be sets and let f be a function from X to Y.
Elements x1 and x2 of X are equivalent if f(x1) and f(x2) are equal, i.e. are the same element of Y.
The kernel of f is the equivalence relation thus defined.
The kernel, in the equivalence-relation sense, may be denoted "=f" (or a variation) and may be defined symbolically as
Properties
Like any equivalence relation, the kernel can be modded outIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
to form a quotient set, and the quotient set is the partition:
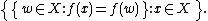
This quotient set X/=f is called the coimage
Coimage
In algebra, the coimage of a homomorphismis the quotientof domain and kernel.The coimage is canonically isomorphic to the image by the first isomorphism theorem, when that theorem applies....
of the function f, and denoted "coim f" (or a variation).
The coimage is naturally isomorphic (in the set-theoretic sense of a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
) to the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
, im f; specifically, the equivalence class of x in X (which is an element of coim f) corresponds to f(x) in Y (which is an element of im f).
Like any binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
, the kernel of a function may be thought of as a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
X × X.
In this guise, the kernel may be denoted "ker f" (or a variation) and may be defined symbolically as
But this is not useful merely as a formalisation in set theory!
In fact, the study of the properties of this subset can shed important light on the function in question.
We give here two examples.
First, if X and Y are algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s of some fixed type (such as group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s, rings, or vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s), and if the function f from X to Y is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
, then ker f will be a subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
X × X. Subalgebras of X × X that are also equivalence relations (called congruence relation
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
s) are important in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, because they define the most general notion of quotient algebra
Quotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
. Thus the coimage of f is a quotient algebra of X much as the image of f is a subalgebra of Y; and the bijection between them becomes an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
in the algebraic sense as well (this is the most general form of the first isomorphism theorem in algebra). The use of kernels in this context is discussed further in the article Kernel (algebra)
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
.
Secondly, if X and Y are topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s and f is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
between them, then the topological properties of ker f can shed light on the spaces X and Y.
For example, if Y is a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, then ker f must be a closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
.
Conversely, if X is a Hausdorff space and ker f is a closed set, then the coimage of f, if given the quotient space topology, must also be a Hausdorff space.