Image (category theory)
Encyclopedia
Given a category
C and a morphism
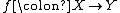in C, the image of f is a monomorphism
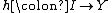satisfying the following universal property
:
The image of f is often denoted by im f or Im(f).
One can show that a morphism f is monic
if and only if f = im f.
the image of a morphism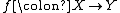
is the inclusion from the ordinary image
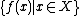to 
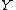. In many concrete categories
such as groups
, abelian groups
and (left- or right) modules
, the image of a morphism is the image of the correspondent morphism in the category of sets.
In any normal category with a zero object and kernels
and cokernels for every morphism, the image of a morphism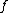
can be expressed as follows:
This holds especially in abelian categories
.
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
C and a morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
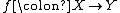in C, the image of f is a monomorphismMonomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
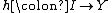satisfying the following universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
:
- There exists a morphism
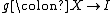such that f = hg. - For any object Z with a morphism
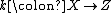and a monomorphism 
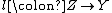such that f = lk, there exists a unique morphism 
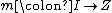such that k = mg and h = lm.
The image of f is often denoted by im f or Im(f).
One can show that a morphism f is monic
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
if and only if f = im f.
Examples
In the category of setsCategory of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
the image of a morphism
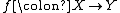is the inclusion from the ordinary imageImage (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
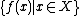to 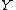. In many concrete categoriesConcrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
such as groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
and (left- or right) modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, the image of a morphism is the image of the correspondent morphism in the category of sets.
In any normal category with a zero object and kernels
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
and cokernels for every morphism, the image of a morphism
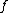can be expressed as follows:- im f = ker coker f
This holds especially in abelian categories
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.