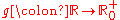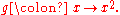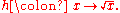In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the codomain or target set of a function

Function (mathematics)

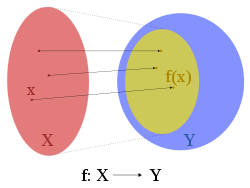
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 is the set into which all of the output of the function is constrained to fall. It is the set in the notation . The codomain is also sometimes referred to as the range

Range (mathematics)

In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...

 but that term is ambiguous as it may also refer to the image

Image (mathematics)

In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...

.

The codomain is part of the modern definition of a function as a triple , with a subset of the Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

 . The set of all elements of the form , where ranges over the elements of the domain , is called the image

Image (mathematics)

In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...

 of . In general, the image of a function is a subset of its codomain. Thus, it may not coincide with its codomain. Namely, a function that is not surjective

Surjective function

In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...

 has elements in its codomain for which the equation does not have a solution.

An older definition of functions that does not include a codomain is also widely used. For example in set theory it is desirable to permit the domain of a function to be a proper class

Class (set theory)

In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...

 , in which case there is formally no such thing as a triple . With such a definition functions do not have a codomain, although some authors still use it informally after introducing a function in the form .

Examples

For a function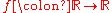


defined by
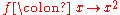, or equivalently ,

the codomain of is , but does not map to any negative number.
Thus the image of is the set 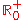; i.e., the interval

Interval (mathematics)

In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...

 .

An alternative function is defined thus:

While and map a given to the same number, they are not, in the modern view, the same function because they have different codomains. A third function can be defined to demonstrate why:

The domain of must be defined to be :

.

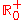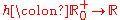The compositions

Function composition

In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...

 are defined
,.

On inspection, is not useful. It is true, unless defined otherwise, that the image of is not known; it is only known that it is a subset of . For this reason, it is possible that , when composed on , might receive an argument for which no output is defined – negative numbers are not elements of the domain of , which is the square root function.

Function composition therefore is a useful notation only when the codomain of the function on the right side of a composition (not its image, which is a consequence of the function and could be unknown at the level of the composition) is the same as the domain of the function on the left side.

The codomain affects whether a function is a surjection, in that the function is surjective if and only if its codomain equals its image. In the example, is a surjection while is not. The codomain does not affect whether a function is an injection

Injective function

In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...

.

A second example of the difference between codomain and image is demonstrated by the linear transformation

Linear transformation

In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...

s between two vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

s – in particular, all the linear transformations from to itself, which can be represented by the matrices

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

 with real coefficients. Each matrix represents a map with the domain and codomain . However, the image is uncertain. Some transformations may have image equal to the whole codomain (in this case the matrices with rank

Rank (linear algebra)

The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...

 ) but many do not, instead mapping into some smaller subspace

Linear subspace

The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....

(the matrices with rank or ). Take for example the matrix given by
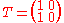
which represents a linear transformation that maps the point to . The point is not in the image of , but is still in the codomain since linear transformations from to are of explicit relevance. Just like all matrices, represents a member of that set. Examining the differences between the image and codomain can often be useful for discovering properties of the function in question. For example, it can be concluded that does not have full rank since its image is smaller than the whole codomain.