
Flat (geometry)
Encyclopedia
In geometry
, a flat is a subset of n-dimensional space that is congruent
to a Euclidean space
of lower dimension
. The flats in two-dimensional space are points and lines
, and the flats in three-dimensional space
are points, lines, and planes
.
In n-dimensional space, there are flats of every dimension from 0 to n – 1. Flats of dimension n – 1 are called hyperplane
s.
Flats are similar to Euclidean subspace
s, except that they need not pass through the origin
. If Euclidean space is considered as an affine space
, the flats are precisely the affine subspaces. Flats are important in linear algebra
, where they provide a geometric realization of the solution set for a system of linear equations.
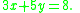
In three-dimensional space, a single linear equation involving x, y, and z defines a plane, while a pair of linear equations can be used to describe a line. In general, a linear equation in n variables describes a hyperplane, and a system of linear equations describes the intersection
of those hyperplanes. Assuming the equations are consistent and linearly independent, a system of k equations describes a flat of dimension n – k.
A flat can also be described by a system of linear parametric equation
s. A line can be described by equations involving one parameter
:
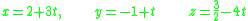
while the description of a plane would require two parameters:
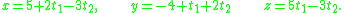
In general, a parameterization of a flat of dimension k would require parameters t1, ..., tk.
Systematic coordinates for flats in any dimension build on either joins or meets, leading to Grassmann coordinates
or dual Grassmann coordinates. For example, a line in three-dimensional space is determined by two distinct points or by two distinct planes. (If the planes are parallel, the ambient space must be a projective space
to accommodate a line "at infinity".)
A flat is also called a linear manifold or linear variety.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a flat is a subset of n-dimensional space that is congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
to a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of lower dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
. The flats in two-dimensional space are points and lines
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, and the flats in three-dimensional space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
are points, lines, and planes
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
.
In n-dimensional space, there are flats of every dimension from 0 to n – 1. Flats of dimension n – 1 are called hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s.
Flats are similar to Euclidean subspace
Euclidean subspace
In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
s, except that they need not pass through the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
. If Euclidean space is considered as an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, the flats are precisely the affine subspaces. Flats are important in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, where they provide a geometric realization of the solution set for a system of linear equations.
Description
A flat can be described by a system of linear equations. For example, a line in two-dimensional space can be described by a single linear equation involving x and y: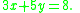
In three-dimensional space, a single linear equation involving x, y, and z defines a plane, while a pair of linear equations can be used to describe a line. In general, a linear equation in n variables describes a hyperplane, and a system of linear equations describes the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of those hyperplanes. Assuming the equations are consistent and linearly independent, a system of k equations describes a flat of dimension n – k.
A flat can also be described by a system of linear parametric equation
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
s. A line can be described by equations involving one parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
:
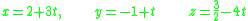
while the description of a plane would require two parameters:
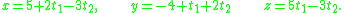
In general, a parameterization of a flat of dimension k would require parameters t1, ..., tk.
Systematic coordinates for flats in any dimension build on either joins or meets, leading to Grassmann coordinates
Plücker coordinates
In geometry, Plücker coordinates, introduced by Julius Plücker in the 19th century, are a way to assign six homogenous coordinates to each line in projective 3-space, P3. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines...
or dual Grassmann coordinates. For example, a line in three-dimensional space is determined by two distinct points or by two distinct planes. (If the planes are parallel, the ambient space must be a projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
to accommodate a line "at infinity".)
A flat is also called a linear manifold or linear variety.

