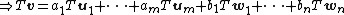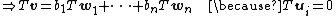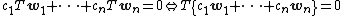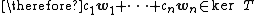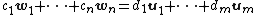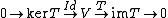Rank-nullity theorem
Encyclopedia
In mathematics
, the rank–nullity theorem of linear algebra
, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix (with m rows and n columns) over some field
, then
This applies to linear maps as well. Let V and W be vector space
s over some field and let T : V → W be a linear map. Then the rank of T is the dimension
of the image of T and the nullity of T is the dimension of the kernel
of T, so we have
or, equivalently,
This is in fact more general than the matrix statement above, because here V and W may even be infinite-dimensional.
One can refine this statement (via the splitting lemma
or the below proof) to be a statement about an isomorphism
of spaces, not just dimensions: in addition to: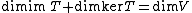
one in fact also has: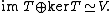
More generally, one can consider the image, kernel, coimage, and cokernel, which are related by the fundamental theorem of linear algebra
.
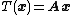 , where
, where 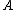 is
is 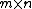 . The second proof looks at the homogeneous system
. The second proof looks at the homogeneous system 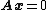 associated with an
associated with an 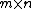 matrix
matrix 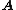 of rank
of rank
 and shows explicitly that there exist a set of
and shows explicitly that there exist a set of  linearly independent solutions that span the null space of
linearly independent solutions that span the null space of 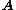 .
.
First proof: Suppose forms a basis of ker T. We can extend this to form a basis of V:
forms a basis of ker T. We can extend this to form a basis of V: 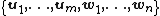 .
.
Since the dimension of ker T is m and the dimension of V is m+n, it suffices to show that the dimension of image T is n.
Let us see that is a basis of image T.
is a basis of image T.
Let v be an arbitrary vector in V. There exist unique scalars such that:
Thus, spans image T.
spans image T.
We only now need to show that this list is not redundant; that is, that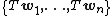 are linearly independent. We can do this by showing that a linear combination of these vectors is zero if and only if the coefficient on each vector is zero. Let:
are linearly independent. We can do this by showing that a linear combination of these vectors is zero if and only if the coefficient on each vector is zero. Let:
Then, since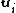 span ker T, there exists a set of scalars
span ker T, there exists a set of scalars 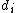 such that:
such that:
But, since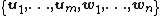 form a basis of V, all
form a basis of V, all 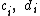 must be zero.
must be zero.
Therefore, is linearly independent and indeed a basis of image T. This proves that the dimension of image T is n, as desired.
is linearly independent and indeed a basis of image T. This proves that the dimension of image T is n, as desired.
In more abstract terms, the map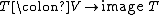 splits.
splits.
Second proof: Let be an
be an 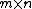 matrix with
matrix with  linearly independent columns (i.e. rank of
linearly independent columns (i.e. rank of 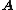 is
is  ). We will show that: (i) there exists a set of
). We will show that: (i) there exists a set of  linearly independent solutions to the homogeneous system
linearly independent solutions to the homogeneous system 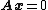 , and (ii) that every other solution is a linear combination of these
, and (ii) that every other solution is a linear combination of these  solutions. In other words, we will produce an
solutions. In other words, we will produce an 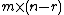 matrix
matrix 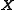 whose columns form a basis
whose columns form a basis
of the null space of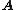 .
.
Without loss of generality, assume that the first columns of
columns of 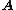 are linearly independent. So, we can write
are linearly independent. So, we can write 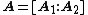 , where
, where  is
is 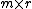 with
with  linearly independent column vectors and
linearly independent column vectors and 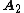 is
is 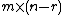 , each of whose
, each of whose  columns are linear combinations of the columns of
columns are linear combinations of the columns of 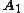 . This means that
. This means that 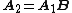 for some
for some 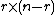 matrix
matrix  (see rank factorization
(see rank factorization
) and, hence,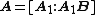 .
.
Let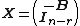 , where
, where 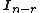 is the
is the 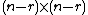 identity matrix
identity matrix
. We note that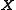 is an
is an 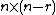 matrix that satisfies
matrix that satisfies
Therefore, each of the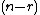 columns of
columns of 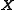 are particular solutions of
are particular solutions of 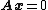 . Furthermore, the
. Furthermore, the  columns of
columns of 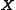 are linearly independent because
are linearly independent because  will imply
will imply  :
: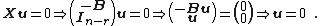
Therefore, the column vectors of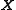 constitute a set of
constitute a set of  linearly independent solutions for
linearly independent solutions for  .
.
We next prove that any solution of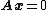 must be a linear combination
must be a linear combination
of the columns of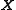 . For this, let
. For this, let 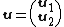 be any vector such that
be any vector such that  . Note that since the columns of
. Note that since the columns of 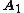 are linearly independent,
are linearly independent, 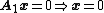 . Therefore,
. Therefore,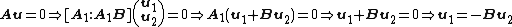
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the rank–nullity theorem of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix (with m rows and n columns) over some field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, then
- rank A + nullity A = n.
This applies to linear maps as well. Let V and W be vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over some field and let T : V → W be a linear map. Then the rank of T is the dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of the image of T and the nullity of T is the dimension of the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of T, so we have
- dim (im T) + dim (ker T) = dim V
or, equivalently,
- rank T + nullity T = dim V.
This is in fact more general than the matrix statement above, because here V and W may even be infinite-dimensional.
One can refine this statement (via the splitting lemma
Splitting lemma
In mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
or the below proof) to be a statement about an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of spaces, not just dimensions: in addition to:
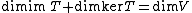
one in fact also has:
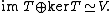
More generally, one can consider the image, kernel, coimage, and cokernel, which are related by the fundamental theorem of linear algebra
Fundamental theorem of linear algebra
In mathematics, the fundamental theorem of linear algebra makes several statements regarding vector spaces. These may be stated concretely in terms of the rank r of an m×n matrix A and its singular value decomposition:A=U\Sigma V^T\...
.
Proofs
We give two proofs. The first proof uses notations for linear transformations, but can be easily adapted to matrices by writing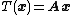 , where
, where 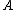 is
is 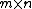 . The second proof looks at the homogeneous system
. The second proof looks at the homogeneous system 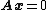 associated with an
associated with an 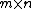 matrix
matrix 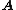 of rank
of rankRank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
 and shows explicitly that there exist a set of
and shows explicitly that there exist a set of  linearly independent solutions that span the null space of
linearly independent solutions that span the null space of 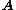 .
.First proof: Suppose
 forms a basis of ker T. We can extend this to form a basis of V:
forms a basis of ker T. We can extend this to form a basis of V: 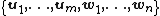 .
.Since the dimension of ker T is m and the dimension of V is m+n, it suffices to show that the dimension of image T is n.
Let us see that
 is a basis of image T.
is a basis of image T.Let v be an arbitrary vector in V. There exist unique scalars such that:
Thus,
 spans image T.
spans image T.We only now need to show that this list is not redundant; that is, that
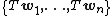 are linearly independent. We can do this by showing that a linear combination of these vectors is zero if and only if the coefficient on each vector is zero. Let:
are linearly independent. We can do this by showing that a linear combination of these vectors is zero if and only if the coefficient on each vector is zero. Let:Then, since
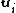 span ker T, there exists a set of scalars
span ker T, there exists a set of scalars 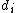 such that:
such that:But, since
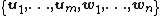 form a basis of V, all
form a basis of V, all 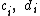 must be zero.
must be zero.Therefore,
 is linearly independent and indeed a basis of image T. This proves that the dimension of image T is n, as desired.
is linearly independent and indeed a basis of image T. This proves that the dimension of image T is n, as desired.In more abstract terms, the map
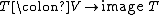 splits.
splits.Second proof: Let
 be an
be an 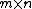 matrix with
matrix with  linearly independent columns (i.e. rank of
linearly independent columns (i.e. rank of 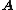 is
is  ). We will show that: (i) there exists a set of
). We will show that: (i) there exists a set of  linearly independent solutions to the homogeneous system
linearly independent solutions to the homogeneous system 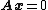 , and (ii) that every other solution is a linear combination of these
, and (ii) that every other solution is a linear combination of these  solutions. In other words, we will produce an
solutions. In other words, we will produce an 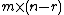 matrix
matrix 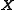 whose columns form a basis
whose columns form a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of the null space of
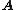 .
.Without loss of generality, assume that the first
 columns of
columns of 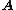 are linearly independent. So, we can write
are linearly independent. So, we can write 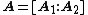 , where
, where  is
is 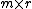 with
with  linearly independent column vectors and
linearly independent column vectors and 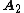 is
is 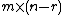 , each of whose
, each of whose  columns are linear combinations of the columns of
columns are linear combinations of the columns of 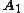 . This means that
. This means that 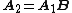 for some
for some 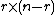 matrix
matrix  (see rank factorization
(see rank factorizationRank factorization
Given an m \times n matrix A of rank r, a rank decomposition or rank factorization of A is a product A=CF, where C is an m \times r matrix and F is an r \times n matrix....
) and, hence,
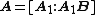 .
.Let
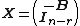 , where
, where 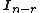 is the
is the 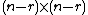 identity matrix
identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. We note that
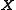 is an
is an 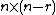 matrix that satisfies
matrix that satisfies
Therefore, each of the
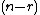 columns of
columns of 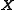 are particular solutions of
are particular solutions of 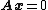 . Furthermore, the
. Furthermore, the  columns of
columns of 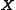 are linearly independent because
are linearly independent because  will imply
will imply  :
: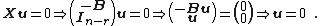
Therefore, the column vectors of
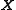 constitute a set of
constitute a set of  linearly independent solutions for
linearly independent solutions for  .
.We next prove that any solution of
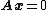 must be a linear combination
must be a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the columns of
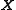 . For this, let
. For this, let 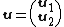 be any vector such that
be any vector such that  . Note that since the columns of
. Note that since the columns of 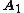 are linearly independent,
are linearly independent, 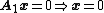 . Therefore,
. Therefore,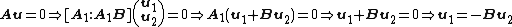
-
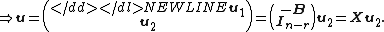
This proves that any vector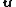 that is a solution of
that is a solution of 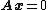 must be a linear combination of the
must be a linear combination of the  special solutions given by the columns of
special solutions given by the columns of 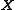 . And we have already seen that the columns of
. And we have already seen that the columns of 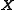 are linearly independent. Hence, the columns of
are linearly independent. Hence, the columns of 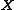 constitute a basis for the null spaceNull spaceIn linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
constitute a basis for the null spaceNull spaceIn linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of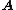 . Therefore, the nullity of
. Therefore, the nullity of 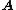 is
is  . Since
. Since  equals rank of
equals rank of 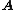 , it follows that rank(
, it follows that rank(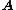 ) + nullity(
) + nullity(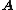 ) =
) =  . QED.
. QED.
Reformulations and generalizations
This theorem is a statement of the first isomorphism theorem of algebra to the case of vector spaces; it generalizes to the splitting lemmaSplitting lemmaIn mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
.
In more modern language, the theorem can also be phrased as follows: if- 0 → U → V → R → 0
is a short exact sequence of vector spaces, then- dim(U) + dim(R) = dim(V).
Here R plays the role of im T and U is ker T, i.e.
.
In the finite-dimensional case, this formulation is susceptible to a generalization: if- 0 → V1 → V2 → ... → Vr → 0
is an exact sequenceExact sequenceAn exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
of finite-dimensional vector spaces, then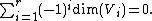
The rank–nullity theorem for finite-dimensional vector spaces may also be formulated in terms of the index of a linear map. The index of a linear map T : V → W, where V and W are finite-dimensional, is defined by
- index T = dim(ker T) − dim(cokerCokernelIn mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
T).
Intuitively, dim(ker T) is the number of independent solutions x of the equation Tx = 0, and dim(coker T) is the number of independent restrictions that have to be put on y to make Tx = y solvable. The rank–nullity theorem for finite-dimensional vector spaces is equivalent to the statement
- index T = dim(V) − dim(W).
We see that we can easily read off the index of the linear map T from the involved spaces, without any need to analyze T in detail. This effect also occurs in a much deeper result: the Atiyah–Singer index theoremAtiyah–Singer index theoremIn differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index...
states that the index of certain differential operators can be read off the geometry of the involved spaces.