
Splitting lemma
Encyclopedia
In mathematics
, and more specifically in homological algebra
, the splitting lemma states that in any abelian category
, the following statements for short exact sequence are equivalent.
Given a short exact sequence with maps q and r: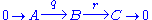
one writes the additional arrows t and u for maps that may not exist: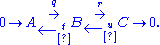
Then the following are equivalent:
1. left split: there exists a map t: B → A such that tq is the identity
on A,
2. right split: there exists a map u: C → B such that ru is the identity on C,
3. direct sum: B is isomorphic to the direct sum
of A and C, with q being the natural injection of A and r being the natural projection onto C.
The short exact sequence is called split if any of the above statements hold.
It allows one to refine the first isomorphism theorem:
It is a categorical generalization of the rank–nullity theorem (in the form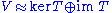 ) in linear algebra
) in linear algebra
.
To prove that (1) implies (3), first note that any member of B is in the set (ker
t + im
q). This follows since for all b in B, b = (b - qt(b)) + qt(b); qt(b) is obviously in im q, and (b - qt(b)) is in ker t, since
Next, the intersection of im q and ker t is 0, since if there exists a in A such that q(a) = b, and t(b) = 0, then 0 = tq(a) = a; and therefore, b = 0.
This proves that B is the direct sum of im q and ker t. So, for all b in B, b can be uniquely identified by some a in A, k in ker t, such that b = q(a) + k.
By exactness ker r = im q. The subsequence B → C → 0 implies that r is onto; therefore for any c in C there exists some b = q(a) + k such that c = r(b) = r(q(a) + k) = r(k). Therefore, for any c in C, exists k in ker t such that c = r(k), and r(ker t) = C.
If r(k) = 0, then k is in im q; since the intersection of im q and ker t = 0, then k = 0. Therefore the restriction of the morphism r : ker t → C is an isomorphism; and ker t is isomorphic to C.
Finally, im q is isomorphic to A due to the exactness of 0 → A → B; so B is isomorphic to the direct sum of A and C, which proves (3).
To show that (2) implies (3), we follow a similar argument. Any member of B is in the set ker r + im u; since for all b in B, b = (b - ur(b)) + ur(b), which is in ker r + im u. The intersection of ker r and im u is 0, since if r(b) = 0 and u(c) = b, then 0 = ru(c) = c.
By exactness, im q = ker r, and since q is an injection, im q is isomorphic to A, so A is isomorphic to ker r. Since ru is a bijection, u is an injection, and thus im u is isomorphic to C. So B is again the direct sum of A and C.
, which is not an abelian category.
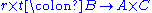 gives an isomorphism, so B is a direct sum (condition 3), and thus inverting the isomorphism and composing with the natural injection
gives an isomorphism, so B is a direct sum (condition 3), and thus inverting the isomorphism and composing with the natural injection 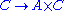 gives an injection
gives an injection  splitting r (condition 2).
splitting r (condition 2).
However, if a short exact sequence of groups is right split (condition 2), then it need not be left split or a direct sum (neither condition 1 nor 3 follows): the problem is that the image of the right splitting need not be normal. What is true in this case is that B is a semidirect product
, though not in general a direct product.
 , the symmetric group on three letters. Let A denote the alternating subgroup, and let
, the symmetric group on three letters. Let A denote the alternating subgroup, and let 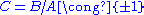 . Let q and r denote the inclusion map and the sign (mathematics)
. Let q and r denote the inclusion map and the sign (mathematics)
map respectively, so that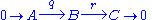
is a short exact sequence. Condition (3) fails, because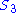 is not abelian. But condition (2) holds: we may define u: C → B by mapping the generator to any two-cycle. Note for completeness that condition (1) fails: any map t: B → A must map every two-cycle to the identity because the map has to be a group homomorphism
is not abelian. But condition (2) holds: we may define u: C → B by mapping the generator to any two-cycle. Note for completeness that condition (1) fails: any map t: B → A must map every two-cycle to the identity because the map has to be a group homomorphism
, while the order of a two-cycle is 2 which can not be divided by the order of the elements in A other than the identity element, which is 3 as A is the alternating subgroup of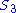 , or namely the cyclic group of order 3. But every permutation is a product of two-cycles, so t is the trivial map, whence tq: A → A is the trivial map, not the identity.
, or namely the cyclic group of order 3. But every permutation is a product of two-cycles, so t is the trivial map, whence tq: A → A is the trivial map, not the identity.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and more specifically in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, the splitting lemma states that in any abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, the following statements for short exact sequence are equivalent.
Given a short exact sequence with maps q and r:
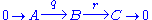
one writes the additional arrows t and u for maps that may not exist:
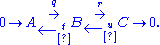
Then the following are equivalent:
1. left split: there exists a map t: B → A such that tq is the identity
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on A,
2. right split: there exists a map u: C → B such that ru is the identity on C,
3. direct sum: B is isomorphic to the direct sum
Biproduct
In category theory and its applications to mathematics, a biproduct of a finite collection of objects in a category with zero object is both a product and a coproduct. In a preadditive category the notions of product and coproduct coincide for finite collections of objects...
of A and C, with q being the natural injection of A and r being the natural projection onto C.
The short exact sequence is called split if any of the above statements hold.
It allows one to refine the first isomorphism theorem:
- the first isomorphism theorem states that in the above short exact sequence,
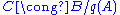
- if the sequence splits, then
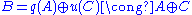 , and the first isomorphism theorem is just the projection onto C.
, and the first isomorphism theorem is just the projection onto C.
It is a categorical generalization of the rank–nullity theorem (in the form
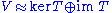 ) in linear algebra
) in linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
.
Proof
First, to show that (3) implies both (1) and (2), we assume (3) and take as t the natural projection of the direct sum onto A, and take as u the natural injection of C into the direct sum.To prove that (1) implies (3), first note that any member of B is in the set (ker
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
t + im
Image
An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...
q). This follows since for all b in B, b = (b - qt(b)) + qt(b); qt(b) is obviously in im q, and (b - qt(b)) is in ker t, since
- t(b - qt(b)) = t(b) - tqt(b) = t(b) - (tq)t(b) = t(b) - t(b) = 0.
Next, the intersection of im q and ker t is 0, since if there exists a in A such that q(a) = b, and t(b) = 0, then 0 = tq(a) = a; and therefore, b = 0.
This proves that B is the direct sum of im q and ker t. So, for all b in B, b can be uniquely identified by some a in A, k in ker t, such that b = q(a) + k.
By exactness ker r = im q. The subsequence B → C → 0 implies that r is onto; therefore for any c in C there exists some b = q(a) + k such that c = r(b) = r(q(a) + k) = r(k). Therefore, for any c in C, exists k in ker t such that c = r(k), and r(ker t) = C.
If r(k) = 0, then k is in im q; since the intersection of im q and ker t = 0, then k = 0. Therefore the restriction of the morphism r : ker t → C is an isomorphism; and ker t is isomorphic to C.
Finally, im q is isomorphic to A due to the exactness of 0 → A → B; so B is isomorphic to the direct sum of A and C, which proves (3).
To show that (2) implies (3), we follow a similar argument. Any member of B is in the set ker r + im u; since for all b in B, b = (b - ur(b)) + ur(b), which is in ker r + im u. The intersection of ker r and im u is 0, since if r(b) = 0 and u(c) = b, then 0 = ru(c) = c.
By exactness, im q = ker r, and since q is an injection, im q is isomorphic to A, so A is isomorphic to ker r. Since ru is a bijection, u is an injection, and thus im u is isomorphic to C. So B is again the direct sum of A and C.
Non-abelian groups
In the form stated here, the splitting lemma does not hold in the full category of groupsCategory of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, which is not an abelian category.
Partially true
It is partially true: if a short exact sequence of groups is left split or a direct sum (conditions 1 or 3), then all of the conditions hold. For a direct sum this is clear, as one can inject from or project to the summands. For a left split sequence, the map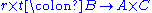 gives an isomorphism, so B is a direct sum (condition 3), and thus inverting the isomorphism and composing with the natural injection
gives an isomorphism, so B is a direct sum (condition 3), and thus inverting the isomorphism and composing with the natural injection 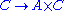 gives an injection
gives an injection  splitting r (condition 2).
splitting r (condition 2).However, if a short exact sequence of groups is right split (condition 2), then it need not be left split or a direct sum (neither condition 1 nor 3 follows): the problem is that the image of the right splitting need not be normal. What is true in this case is that B is a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
, though not in general a direct product.
Counterexample
To form a counterexample, take the smallest non-abelian group , the symmetric group on three letters. Let A denote the alternating subgroup, and let
, the symmetric group on three letters. Let A denote the alternating subgroup, and let 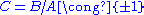 . Let q and r denote the inclusion map and the sign (mathematics)
. Let q and r denote the inclusion map and the sign (mathematics)Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
map respectively, so that
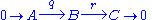
is a short exact sequence. Condition (3) fails, because
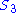 is not abelian. But condition (2) holds: we may define u: C → B by mapping the generator to any two-cycle. Note for completeness that condition (1) fails: any map t: B → A must map every two-cycle to the identity because the map has to be a group homomorphism
is not abelian. But condition (2) holds: we may define u: C → B by mapping the generator to any two-cycle. Note for completeness that condition (1) fails: any map t: B → A must map every two-cycle to the identity because the map has to be a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
, while the order of a two-cycle is 2 which can not be divided by the order of the elements in A other than the identity element, which is 3 as A is the alternating subgroup of
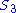 , or namely the cyclic group of order 3. But every permutation is a product of two-cycles, so t is the trivial map, whence tq: A → A is the trivial map, not the identity.
, or namely the cyclic group of order 3. But every permutation is a product of two-cycles, so t is the trivial map, whence tq: A → A is the trivial map, not the identity.

