Symmetric matrix
Encyclopedia
In linear algebra
, a symmetric matrix is a square matrix that is equal to its transpose
. Let A be a symmetric matrix. Then:
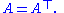
The entries of a symmetric matrix are symmetric with respect to the main diagonal (top left to bottom right). So if the entries are written as A = (aij), then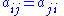
for all indices i and j. The following 3×3 matrix is symmetric:
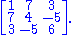
Every diagonal matrix
is symmetric, since all off-diagonal entries are zero. Similarly, each diagonal element of a skew-symmetric matrix
must be zero, since each is its own negative.
In linear algebra, a real
symmetric matrix represents a self-adjoint operator
over a real
inner product space
. The corresponding object for a complex
inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose
. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric matrix refers to one which has real-valued entries. Symmetric matrices appear naturally in a variety of applications, and typical numerical linear algebra software makes special accommodations for them.
says that any symmetric matrix whose entries are real
can be diagonalized
by an orthogonal matrix
. More explicitly: For every symmetric real matrix A there exists a real orthogonal matrix Q such that D = QTAQ is a diagonal matrix
. Every symmetric matrix is thus, up to
choice of an orthonormal basis
, a diagonal matrix.
Another way phrase the spectral theorem is that a real n×n matrix A is symmetric if and only there is an orthonormal basis of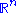
consisting of eigenvectors for A.
Every real symmetric matrix is Hermitian, and therefore all its eigenvalues are real. (In fact, the eigenvalues are the entries in the above diagonal matrix D, and therefore D is uniquely determined by A up to the order of its entries.) Essentially, the property of being symmetric for real matrices corresponds to the property of being Hermitian for complex matrices.
A complex symmetric matrix A can always be diagonalized in the form D = UT A U, where D is complex diagonal and U is not Hermitian but complex orthogonal with UT U = I. In this case the columns of U are the eigenvectors of A and the diagonal elements of D are eigenvalues.
The sum and difference of two symmetric matrices is again symmetric, but this is not always true for the product
: given symmetric matrices A and B, then AB is symmetric if and only if A and B commute
, i.e., if AB = BA. So for integer n, An is symmetric if A is symmetric. Two real symmetric matrices commute if and only if they have the same eigenspaces.
If A−1 exists, it is symmetric if and only if A is symmetric.
Let Matn denote the space of matrices. A symmetric n × n matrix is determined by n(n + 1)/2 scalars (the number of entries on or above the main diagonal). Similarly, a skew-symmetric matrix
is determined by n(n − 1)/2 scalars (the number of entries above the main diagonal). If Symn denotes the space of symmetric matrices and Skewn the space of skew-symmetric matrices then since and }, i.e.
where ⊕ denotes the direct sum
. Let then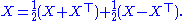
Notice that and This is true for every square matrix X with entries from any field
whose characteristic
is different from 2.
Any matrix congruent
to a symmetric matrix is again symmetric: if X is a symmetric matrix then so is AXAT for any matrix A.
Denote with
the standard inner product on Rn. The real n-by-n matrix A is symmetric if and only if
Since this definition is independent of the choice of basis
, symmetry is a property that depends only on the linear operator A and a choice of inner product. This characterization of symmetry is useful, for example, in differential geometry, for each tangent space
to a manifold
may be endowed with an inner product, giving rise to what is called a Riemannian manifold
. Another area where this formulation is used is in Hilbert space
s.
A symmetric matrix is a normal matrix
.
, one can prove that every square real matrix can be written as a product of two real symmetric matrices, and every square complex matrix can be written as a product of two complex symmetric matrices.
Every real non-singular matrix can be uniquely factored as the product of an orthogonal matrix
and a symmetric positive definite matrix, which is called a polar decomposition. Singular matrices can also be factored, but not uniquely.
Cholesky decomposition
states that every real positive-definite symmetric matrix A is a product of a lower-triangular matrix L and its transpose,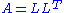
.
If the matrix is symmetric indefinite, it may be still decomposed as
where 
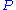is
a permutation matrix (arising from the need to pivot
),
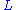a lower unit triangular matrix, 
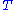a symmetric tridiagonal matrix, and 
a direct sum of symmetric 1×1 and 2×2 blocks.
Every real symmetric matrix A can be diagonalized, moreover the eigen decomposition takes a simpler form:
where Q is an orthogonal matrix
(the columns of which are eigenvectors of A), and Λ is real and diagonal (having the eigenvalues of A on the diagonal).
of twice continuously differentiable functions of n real variables.
Every quadratic form
q on Rn can be uniquely written in the form q(x) = xTAx with a symmetric n-by-n matrix A. Because of the above spectral theorem, one can then say that every quadratic form, up to the choice of an orthonormal basis of Rn, "looks like"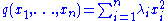
with real numbers λi. This considerably simplifies the study of quadratic forms, as well as the study of the level sets {x : q(x) = 1} which are generalizations of conic section
s.
This is important partly because the second-order behavior of every smooth multi-variable function is described by the quadratic form belonging to the function's Hessian; this is a consequence of Taylor's theorem
.
D and symmetric matrix S such that
The transpose of a symmetrizable matrix is symmetrizable, for A matrix is symmetrizable if and only if the following conditions are met:
or pattern in square matrices have special names; see for example:
See also symmetry in mathematics
.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a symmetric matrix is a square matrix that is equal to its transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
. Let A be a symmetric matrix. Then:
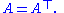
The entries of a symmetric matrix are symmetric with respect to the main diagonal (top left to bottom right). So if the entries are written as A = (aij), then
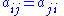
for all indices i and j. The following 3×3 matrix is symmetric:
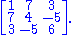
Every diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
is symmetric, since all off-diagonal entries are zero. Similarly, each diagonal element of a skew-symmetric matrix
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
must be zero, since each is its own negative.
In linear algebra, a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
symmetric matrix represents a self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
over a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
. The corresponding object for a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric matrix refers to one which has real-valued entries. Symmetric matrices appear naturally in a variety of applications, and typical numerical linear algebra software makes special accommodations for them.
Properties
The finite-dimensional spectral theoremSpectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
says that any symmetric matrix whose entries are real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
can be diagonalized
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
by an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
. More explicitly: For every symmetric real matrix A there exists a real orthogonal matrix Q such that D = QTAQ is a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. Every symmetric matrix is thus, up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
choice of an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
, a diagonal matrix.
Another way phrase the spectral theorem is that a real n×n matrix A is symmetric if and only there is an orthonormal basis of
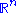consisting of eigenvectors for A.Every real symmetric matrix is Hermitian, and therefore all its eigenvalues are real. (In fact, the eigenvalues are the entries in the above diagonal matrix D, and therefore D is uniquely determined by A up to the order of its entries.) Essentially, the property of being symmetric for real matrices corresponds to the property of being Hermitian for complex matrices.
A complex symmetric matrix A can always be diagonalized in the form D = UT A U, where D is complex diagonal and U is not Hermitian but complex orthogonal with UT U = I. In this case the columns of U are the eigenvectors of A and the diagonal elements of D are eigenvalues.
The sum and difference of two symmetric matrices is again symmetric, but this is not always true for the product
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
: given symmetric matrices A and B, then AB is symmetric if and only if A and B commute
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, i.e., if AB = BA. So for integer n, An is symmetric if A is symmetric. Two real symmetric matrices commute if and only if they have the same eigenspaces.
If A−1 exists, it is symmetric if and only if A is symmetric.
Let Matn denote the space of matrices. A symmetric n × n matrix is determined by n(n + 1)/2 scalars (the number of entries on or above the main diagonal). Similarly, a skew-symmetric matrix
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
is determined by n(n − 1)/2 scalars (the number of entries above the main diagonal). If Symn denotes the space of symmetric matrices and Skewn the space of skew-symmetric matrices then since and }, i.e.
where ⊕ denotes the direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
. Let then
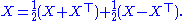
Notice that and This is true for every square matrix X with entries from any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
whose characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
is different from 2.
Any matrix congruent
Matrix congruence
In mathematics, two matrices A and B over a field are called congruent if there exists an invertible matrix P over the same field such thatwhere "T" denotes the matrix transpose...
to a symmetric matrix is again symmetric: if X is a symmetric matrix then so is AXAT for any matrix A.
Denote with
the standard inner product on Rn. The real n-by-n matrix A is symmetric if and only ifSince this definition is independent of the choice of basis
Basis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
, symmetry is a property that depends only on the linear operator A and a choice of inner product. This characterization of symmetry is useful, for example, in differential geometry, for each tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
may be endowed with an inner product, giving rise to what is called a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. Another area where this formulation is used is in Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s.
A symmetric matrix is a normal matrix
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
.
Decomposition
Using the Jordan normal formJordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
, one can prove that every square real matrix can be written as a product of two real symmetric matrices, and every square complex matrix can be written as a product of two complex symmetric matrices.
Every real non-singular matrix can be uniquely factored as the product of an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
and a symmetric positive definite matrix, which is called a polar decomposition. Singular matrices can also be factored, but not uniquely.
Cholesky decomposition
Cholesky decomposition
In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
states that every real positive-definite symmetric matrix A is a product of a lower-triangular matrix L and its transpose,
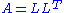.If the matrix is symmetric indefinite, it may be still decomposed as
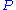where isa permutation matrix (arising from the need to pivot
Pivot element
The pivot or pivot element is the element of a matrix, an array, or some other kind of finite set, which is selected first by an algorithm , to do certain calculations...
),
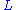a lower unit triangular matrix, 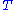a symmetric tridiagonal matrix, and a direct sum of symmetric 1×1 and 2×2 blocks.
Every real symmetric matrix A can be diagonalized, moreover the eigen decomposition takes a simpler form:
where Q is an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(the columns of which are eigenvectors of A), and Λ is real and diagonal (having the eigenvalues of A on the diagonal).
Hessian
Symmetric real n-by-n matrices appear as the HessianHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of twice continuously differentiable functions of n real variables.
Every quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
q on Rn can be uniquely written in the form q(x) = xTAx with a symmetric n-by-n matrix A. Because of the above spectral theorem, one can then say that every quadratic form, up to the choice of an orthonormal basis of Rn, "looks like"
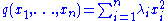
with real numbers λi. This considerably simplifies the study of quadratic forms, as well as the study of the level sets {x : q(x) = 1} which are generalizations of conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s.
This is important partly because the second-order behavior of every smooth multi-variable function is described by the quadratic form belonging to the function's Hessian; this is a consequence of Taylor's theorem
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
.
Symmetrizable matrix
An n-by-n matrix A is said to be symmetrizable if there exist an invertible diagonal matrixDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
D and symmetric matrix S such that
The transpose of a symmetrizable matrix is symmetrizable, for A matrix is symmetrizable if and only if the following conditions are met:
See also
Other types of symmetrySymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
or pattern in square matrices have special names; see for example:
- Antimetric matrix
- Centrosymmetric matrixCentrosymmetric matrixIn mathematics, especially in linear algebra and matrix theory, a centrosymmetric matrix is a matrix which is symmetric about its center. More precisely, an n × n matrix A = [ Ai,j ] is centrosymmetric when its entries satisfy...
- Circulant matrixCirculant matrixIn linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
- Covariance matrixCovariance matrixIn probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
- Coxeter matrix
- Hankel matrix
- Hilbert matrix
- Persymmetric matrixPersymmetric matrixIn mathematics, persymmetric matrix may refer to:# a square matrix which is symmetric in the northeast-to-southwest diagonal; or# a square matrix such that the values on each line perpendicular to the main diagonal are the same for a given line....
- Skew-symmetric matrixSkew-symmetric matrixIn mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
- Toeplitz matrixToeplitz matrixIn linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...
See also symmetry in mathematics
Symmetry in mathematics
Symmetry occurs not only in geometry, but also in other branches of mathematics. It is actually the same as invariance: the property that something does not change under a set of transformations....
.