
Hankel matrix
Encyclopedia
In linear algebra
, a Hankel matrix (or catalecticant matrix), named after Hermann Hankel
, is a square matrix with constant skew-diagonals (positive sloping diagonals), e.g.:
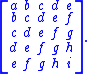
If the i,j element of A is denoted Ai,j, then we have
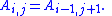
The Hankel matrix is closely related to the Toeplitz matrix
(a Hankel matrix is an upside-down Toeplitz matrix). For a special case of this matrix see Hilbert matrix.
A Hankel operator on a Hilbert space
is one whose matrix with respect to an orthonormal basis
is an infinite Hankel matrix
 , where
, where 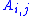 depends only on
depends only on  .
.
The determinant of a Hankel matrix is called a catalecticant
.
, where the transformed sequence corresponds to the determinant of the Hankel matrix. That is, the sequence is the Hankel transform of the sequence
is the Hankel transform of the sequence  when
when
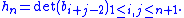
Here,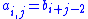 is the Hankel matrix of the sequence
is the Hankel matrix of the sequence  . The Hankel transform is invariant under the binomial transform of a sequence. That is, if one writes
. The Hankel transform is invariant under the binomial transform of a sequence. That is, if one writes
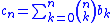
as the binomial transform of the sequence , then one has
, then one has
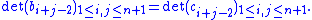
Hankel matrices for system identification
Hankel matrices are formed when given a sequence of output data and a realization of an underlying state-space or hidden Markov model is desired. The singular value decomposition
of the Hankel matrix provides a means of computing the A, B, and C matrices which define the state-space realization.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a Hankel matrix (or catalecticant matrix), named after Hermann Hankel
Hermann Hankel
Hermann Hankel was a German mathematician who was born in Halle, Germany and died in Schramberg , Imperial Germany....
, is a square matrix with constant skew-diagonals (positive sloping diagonals), e.g.:
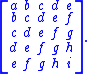
If the i,j element of A is denoted Ai,j, then we have
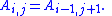
The Hankel matrix is closely related to the Toeplitz matrix
Toeplitz matrix
In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...
(a Hankel matrix is an upside-down Toeplitz matrix). For a special case of this matrix see Hilbert matrix.
A Hankel operator on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is one whose matrix with respect to an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
is an infinite Hankel matrix
 , where
, where 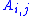 depends only on
depends only on  .
.The determinant of a Hankel matrix is called a catalecticant
Catalecticant
In mathematical invariant theory, the catalecticant of a binary form of degree 2n is a polynomial in its coefficients that vanishes when the binary form is a sum of at most n powers . It was introduced by ; see...
.
Hankel transform
The Hankel transform is the name sometimes given to the transformation of a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
, where the transformed sequence corresponds to the determinant of the Hankel matrix. That is, the sequence
 is the Hankel transform of the sequence
is the Hankel transform of the sequence  when
when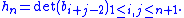
Here,
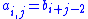 is the Hankel matrix of the sequence
is the Hankel matrix of the sequence  . The Hankel transform is invariant under the binomial transform of a sequence. That is, if one writes
. The Hankel transform is invariant under the binomial transform of a sequence. That is, if one writes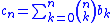
as the binomial transform of the sequence
 , then one has
, then one has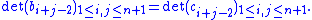
Hankel matrices for system identificationSystem identificationIn control engineering, the field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data...
Hankel matrices are formed when given a sequence of output data and a realization of an underlying state-space or hidden Markov model is desired. The singular value decompositionSingular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
of the Hankel matrix provides a means of computing the A, B, and C matrices which define the state-space realization.

