
Hilbert matrix
Encyclopedia
In linear algebra
, a Hilbert matrix, introduced by , is a square matrix with entries being the unit fraction
s
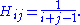
For example, this is the 5 × 5 Hilbert matrix:

The Hilbert matrix can be regarded as derived from the integral
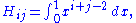
that is, as a Gramian matrix for powers of x. It arises in the least squares
approximation of arbitrary functions by polynomial
s.
The Hilbert matrices are canonical examples of ill-conditioned matrices, making them notoriously difficult to use in numerical computation. For example, the 2-norm condition number
of the matrix above is about 4.8 · 105.
: "Assume that is a real interval. Is it then possible to find a non-zero polynomial P with integral coefficients, such that the integral
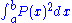
is smaller than any given bound ε > 0, taken arbitrarily small?" To answer this question, Hilbert derives an exact formula for the determinant
of the Hilbert matrices and investigates their asymptotics. He concludes that the answer to his question is positive if the length of the interval is smaller than 4.
. The Hilbert matrix is also totally positive (meaning the determinant of every submatrix is positive).
The Hilbert matrix is an example of a Hankel matrix.
The determinant can be expressed in closed form
, as a special case of the Cauchy determinant. The determinant of the n × n Hilbert matrix is
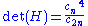
where

Hilbert already mentioned the curious fact that the determinant of the Hilbert matrix is the reciprocal of an integer (see sequence in the OEIS) which also follows from the identity
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a Hilbert matrix, introduced by , is a square matrix with entries being the unit fraction
Unit fraction
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n...
s
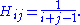
For example, this is the 5 × 5 Hilbert matrix:

The Hilbert matrix can be regarded as derived from the integral
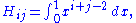
that is, as a Gramian matrix for powers of x. It arises in the least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
approximation of arbitrary functions by polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s.
The Hilbert matrices are canonical examples of ill-conditioned matrices, making them notoriously difficult to use in numerical computation. For example, the 2-norm condition number
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
of the matrix above is about 4.8 · 105.
Historical note
introduced the Hilbert matrix to study the following question in approximation theoryApproximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
: "Assume that is a real interval. Is it then possible to find a non-zero polynomial P with integral coefficients, such that the integral
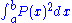
is smaller than any given bound ε > 0, taken arbitrarily small?" To answer this question, Hilbert derives an exact formula for the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the Hilbert matrices and investigates their asymptotics. He concludes that the answer to his question is positive if the length of the interval is smaller than 4.
Properties
The Hilbert matrix is symmetric and positive definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
. The Hilbert matrix is also totally positive (meaning the determinant of every submatrix is positive).
The Hilbert matrix is an example of a Hankel matrix.
The determinant can be expressed in closed form
Closed form
-Maths:* Closed-form expression, a finitary expression* Closed differential form, a differential form \alpha with the property that d\alpha = 0-Poetry:* In poetry analysis, a type of poetry that exhibits regular structure, such as meter or a rhyming pattern;...
, as a special case of the Cauchy determinant. The determinant of the n × n Hilbert matrix is
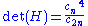
where

Hilbert already mentioned the curious fact that the determinant of the Hilbert matrix is the reciprocal of an integer (see sequence in the OEIS) which also follows from the identity
-
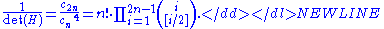
Using Stirling's approximationStirling's approximationIn mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
of the factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
one can establish the following asymptotic result:
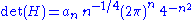
where an converges to the constant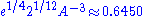 as
as 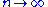 , where A is the Glaisher-Kinkelin constantGlaisher-Kinkelin constantIn mathematics, the Glaisher–Kinkelin constant or Glaisher's constant, typically denoted A, is a mathematical constant, related to the K-function and the Barnes G-function. The constant appears in a number of sums and integrals, especially those involving Gamma functions and zeta functions...
, where A is the Glaisher-Kinkelin constantGlaisher-Kinkelin constantIn mathematics, the Glaisher–Kinkelin constant or Glaisher's constant, typically denoted A, is a mathematical constant, related to the K-function and the Barnes G-function. The constant appears in a number of sums and integrals, especially those involving Gamma functions and zeta functions...
.
The inverse of the Hilbert matrix can be expressed in closed form using binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s; its entries are
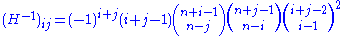
where n is the order of the matrix. It follows that the entries of the inverse matrix are all integer.
The condition number of the n-by-n Hilbert matrix grows as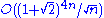 .
.

