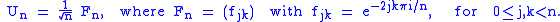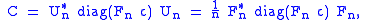Circulant matrix
Encyclopedia
In linear algebra
, a circulant matrix is a special kind of Toeplitz matrix
where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis
, circulant matrices are important because they are diagonalized by a discrete Fourier transform
, and hence linear equation
s that contain them may be quickly solved using a fast Fourier transform
. They can be interpreted analytically as the integral kernel of a convolution operator on the cyclic group
In cryptography
, a circulant matrix is used in the MixColumns step of the Advanced Encryption Standard
.
circulant matrix 
takes the form
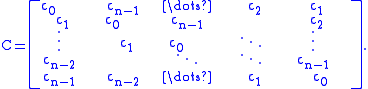
A circulant matrix is fully specified by one vector,
, which appears as the first column of 
. The remaining columns of 
are each cyclic permutation
s of the vector
with offset equal to the column index. The last row of 
is the vector 
in reverse order, and the remaining rows are each cyclic permutation
s of the last row. Note that different sources define the circulant matrix in different ways, for example with the coefficients corresponding to the first row rather than the first column of the matrix, or with a different direction of shift.
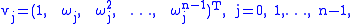
where
are the n-th roots of unity and 
is the imaginary unit
.
The corresponding eigenvalues are then given by
the determinant
of circulant matrix can be computed as: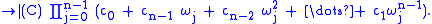
Since taking transpose does not change the eigenvalues of a matrix, an equivalent formulation is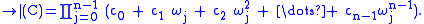
where P is the 'cyclic permutation' matrix given by
where
is a circulant square matrix of size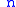 
we can write the equation as the circular convolution
where
is the first column of 
, and the vectors 
, 
and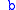 
are cyclically extended in each direction. Using the results of the circular convolution theorem, we can use the discrete Fourier transform
to transform the cyclic convolution into component-wise multiplication
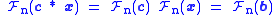
so that
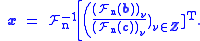
This algorithm is much faster than the standard Gaussian elimination
, especially if a fast Fourier transform
is used.
Consider vectors in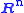
as functions on the integers with period n, (i.e., as periodic bi-infinite sequences: 
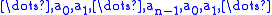) or equivalently, as functions on the cyclic group
of order n, (
or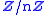 
) geometrically, on (the vertices of) the regular n-gon: this is a discrete analog to periodic functions on the real line or circle.
Then, from the perspective of operator theory
, a circulant matrix is the kernel of a discrete integral transform, namely the convolution operator for the function
this is a discrete circular convolution
. The formula for the convolution of the function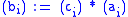s
is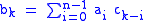
(recall that the sequences are periodic)
which is the product of the vector of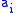
by the circulant matrix.
The discrete Fourier transform then converts convolution into multiplication, which in the matrix setting corresponds to diagonalization.
, a graph
or digraph
whose adjacency matrix
is circulant is called a circulant graph (or digraph). Equivalently, a graph is circulant if its automorphism group contains a full-length cycle. The Möbius ladder
s are examples of circulant graphs, as are the Paley graph
s for fields of prime order.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a circulant matrix is a special kind of Toeplitz matrix
Toeplitz matrix
In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...
where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, circulant matrices are important because they are diagonalized by a discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
, and hence linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
s that contain them may be quickly solved using a fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
. They can be interpreted analytically as the integral kernel of a convolution operator on the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
In cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, a circulant matrix is used in the MixColumns step of the Advanced Encryption Standard
Advanced Encryption Standard
Advanced Encryption Standard is a specification for the encryption of electronic data. It has been adopted by the U.S. government and is now used worldwide. It supersedes DES...
.
Definition
An circulant matrix takes the form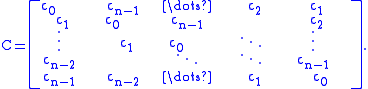A circulant matrix is fully specified by one vector,
, which appears as the first column of . The remaining columns of are each cyclic permutationCyclic permutation
A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...
s of the vector
with offset equal to the column index. The last row of is the vector in reverse order, and the remaining rows are each cyclic permutationCyclic permutation
A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...
s of the last row. Note that different sources define the circulant matrix in different ways, for example with the coefficients corresponding to the first row rather than the first column of the matrix, or with a different direction of shift.
Eigenvectors and eigenvalues
The eigenvectors of a circulant matrix are given by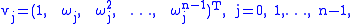where
are the n-th roots of unity and is the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
The corresponding eigenvalues are then given by
Circulant determinant
As a consequence of the explicit formula for the eigenvalues above,the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of circulant matrix can be computed as:
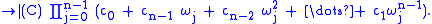
Since taking transpose does not change the eigenvalues of a matrix, an equivalent formulation is
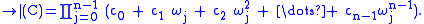
Properties
- We have
where P is the 'cyclic permutation' matrix given by
- The set of
circulant matrices forms an n-dimensional vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
; this can be interpreted as the space of functions on the cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order n,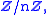
or equivalently the group ringGroup ringIn algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
.
- Circulant matrices form a commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, since for any two given circulant matrices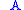
and 
, the sum 
is circulant, the product 
is circulant, and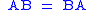 
.
- The eigenvectors of a circulant matrix of a given size are the columns of the unitary discrete Fourier transform matrix of the same size. The latter matrix is defined by
-
- Thus, the matrix
diagonalizesDiagonalizable matrixIn linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
C. In fact, we have - where
is the first column of 
. Thus, the eigenvalues of 
are given by the product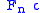 
. This product can be readily calculated by a Fast Fourier transformFast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
.
In linear equations
Given a matrix equationwhere
is a circulant square matrix of size 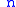we can write the equation as the circular convolutionCircular convolution
The circular convolution, also known as cyclic convolution, of two aperiodic functions occurs when one of them is convolved in the normal way with a periodic summation of the other function. That situation arises in the context of the Circular convolution theorem...
where
is the first column of , and the vectors , and 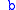are cyclically extended in each direction. Using the results of the circular convolution theorem, we can use the discrete Fourier transformDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
to transform the cyclic convolution into component-wise multiplication
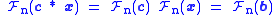
so that
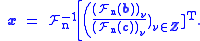
This algorithm is much faster than the standard Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
, especially if a fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
is used.
Analytic interpretation
Circulant matrices can be interpreted geometrically, which explains the connection with the discrete Fourier transform.Consider vectors in
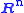as functions on the integers with period n, (i.e., as periodic bi-infinite sequences: ) or equivalently, as functions on the cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order n, (
or 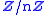) geometrically, on (the vertices of) the regular n-gon: this is a discrete analog to periodic functions on the real line or circle.Then, from the perspective of operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, a circulant matrix is the kernel of a discrete integral transform, namely the convolution operator for the function
this is a discrete circular convolutionCircular convolution
The circular convolution, also known as cyclic convolution, of two aperiodic functions occurs when one of them is convolved in the normal way with a periodic summation of the other function. That situation arises in the context of the Circular convolution theorem...
. The formula for the convolution of the functions
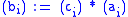is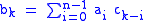 (recall that the sequences are periodic)which is the product of the vector of
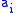by the circulant matrix.The discrete Fourier transform then converts convolution into multiplication, which in the matrix setting corresponds to diagonalization.
Application in graph theory
In graph theoryGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
or digraph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
whose adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
is circulant is called a circulant graph (or digraph). Equivalently, a graph is circulant if its automorphism group contains a full-length cycle. The Möbius ladder
Möbius ladder
In graph theory, the Möbius ladder Mn is a cubic circulant graph with an even number n of vertices, formed from an n-cycle by adding edges connecting opposite pairs of vertices in the cycle...
s are examples of circulant graphs, as are the Paley graph
Paley graph
In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...
s for fields of prime order.
External links
- R. M. Gray, Toeplitz and Circulant Matrices: A Review