Hermitian matrix
Encyclopedia
In mathematics, an Hermitian matrix (or self-adjoint matrix) is a square matrix with complex
entries that is equal to its own conjugate transpose
– that is, the element in the i-th row and j-th column is equal to the complex conjugate
of the element in the j-th row and i-th column, for all indices i and j:
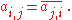
If the conjugate transpose of a matrix
is denoted by 
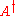, then the Hermitian property can be written concisely as
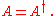
Hermitian matrices can be understood as the complex extension of real symmetric matrices.
Hermitian matrices are named after Charles Hermite
, who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of having eigenvalues always real.
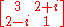
Well-known families of Pauli matrices
, Gell-Mann matrices
and various generalizations are Hermitian. In theoretical physics
such Hermitian matrices usually are multiplied by imaginary
coefficients, which results in skew-Hermitian matrices (see below).
. A matrix that has only real entries is Hermitian if and only if
it is a symmetric matrix, i.e., if it is symmetric with respect to the main diagonal. A real and symmetric matrix is simply a special case of a Hermitian matrix.
Every Hermitian matrix is a normal matrix
, and the finite-dimensional spectral theorem
applies. It says that any Hermitian matrix can be diagonalized
by a unitary matrix, and that the resulting diagonal matrix has only real entries. This implies that all eigenvalues of a Hermitian matrix A are real, and that A has n linearly independent eigenvectors. Moreover, it is possible to find an orthonormal basis
of Cn consisting of n eigenvectors of A.
The sum of any two Hermitian matrices is Hermitian, and the inverse of an invertible Hermitian matrix is Hermitian as well. However, the product
of two Hermitian matrices A and B will only be Hermitian if they commute, i.e., if AB = BA. Thus An is Hermitian if A is Hermitian and n is an integer.
The Hermitian complex n-by-n matrices do not form a vector space
over the complex number
s, since the identity matrix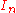
is Hermitian, but 
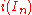is not. However the complex Hermitian matrices do form a vector space over the real numbers. In the 2n2 R dimensional vector space of complex n×n matrices, the complex Hermitian matrices form a subspace of dimension n2. If Ejk denotes the n-by-n matrix with a 1 in the j,k position and zeros elsewhere, a basis can be described as follows:
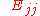for 
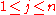(n matrices)
together with the set of matrices of the form
for 
((n2−n)/2 matrices)
and the matrices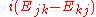
for 
((n2−n)/2 matrices)
where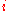
denotes the complex number 
, known as the imaginary unit
.
If n orthonormal eigenvectors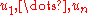
of a Hermitian matrix are chosen and written as the columns of the matrix U, then one eigendecomposition
of A is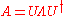
where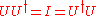 
and therefore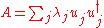
,
where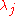
are the eigenvalues on the diagonal of the diagonal matrix 
.
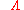Additional facts related to Hermitian matrices include:
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
entries that is equal to its own conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
– that is, the element in the i-th row and j-th column is equal to the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of the element in the j-th row and i-th column, for all indices i and j:
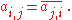
If the conjugate transpose of a matrix
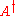is denoted by , then the Hermitian property can be written concisely as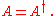Hermitian matrices can be understood as the complex extension of real symmetric matrices.
Hermitian matrices are named after Charles Hermite
Charles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
, who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of having eigenvalues always real.
Examples
For example,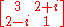Well-known families of Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
, Gell-Mann matrices
Gell-Mann matrices
The Gell-Mann matrices, named for Murray Gell-Mann, are one possible representation of the infinitesimal generators of the special unitary group called SU....
and various generalizations are Hermitian. In theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
such Hermitian matrices usually are multiplied by imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
coefficients, which results in skew-Hermitian matrices (see below).
Properties
The entries on the main diagonal (top left to bottom right) of any Hermitian matrix are necessarily realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. A matrix that has only real entries is Hermitian if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is a symmetric matrix, i.e., if it is symmetric with respect to the main diagonal. A real and symmetric matrix is simply a special case of a Hermitian matrix.
Every Hermitian matrix is a normal matrix
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
, and the finite-dimensional spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
applies. It says that any Hermitian matrix can be diagonalized
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
by a unitary matrix, and that the resulting diagonal matrix has only real entries. This implies that all eigenvalues of a Hermitian matrix A are real, and that A has n linearly independent eigenvectors. Moreover, it is possible to find an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of Cn consisting of n eigenvectors of A.
The sum of any two Hermitian matrices is Hermitian, and the inverse of an invertible Hermitian matrix is Hermitian as well. However, the product
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
of two Hermitian matrices A and B will only be Hermitian if they commute, i.e., if AB = BA. Thus An is Hermitian if A is Hermitian and n is an integer.
The Hermitian complex n-by-n matrices do not form a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, since the identity matrix
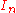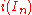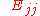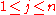is Hermitian, but is not. However the complex Hermitian matrices do form a vector space over the real numbers. In the 2n2 R dimensional vector space of complex n×n matrices, the complex Hermitian matrices form a subspace of dimension n2. If Ejk denotes the n-by-n matrix with a 1 in the j,k position and zeros elsewhere, a basis can be described as follows: for (n matrices)together with the set of matrices of the form
for ((n2−n)/2 matrices)and the matrices
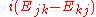for ((n2−n)/2 matrices)where
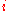denotes the complex number , known as the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
If n orthonormal eigenvectors
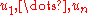of a Hermitian matrix are chosen and written as the columns of the matrix U, then one eigendecompositionEigendecomposition of a matrix
In the mathematical discipline of linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors...
of A is
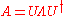where 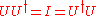and therefore
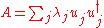,where
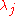are the eigenvalues on the diagonal of the diagonal matrix 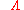.Additional facts related to Hermitian matrices include:
- The sum of a square matrix and its conjugate transpose
is Hermitian. - The difference of a square matrix and its conjugate transpose
is skew-HermitianSkew-Hermitian matrixIn linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...
(also called antihermitian).- This implies that commutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of two Hermitian matrices is skew-Hermitian.
- This implies that commutator
- An arbitrary square matrix C can be written as the sum of a Hermitian matrix A and a skew-Hermitian matrix B:
-
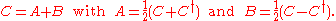
- The determinant of a Hermitian matrix is real:
- Proof:
- Therefore if
See also
- Hermitian form
- Self-adjoint operatorSelf-adjoint operatorIn mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
- Haynsworth inertia additivity formulaHaynsworth inertia additivity formulaIn mathematics, the Haynsworth inertia additivity formula, discovered by Emilie Virginia Haynsworth , concerns the number of positive, negative, and zero eigenvalues of a Hermitian matrix and of block matrices into which it is partitioned....
External links
- Visualizing Hermitian Matrix as An Ellipse with Dr. Geo, by Chao-Kuei Hung from Shu-Te University, gives a more geometric explanation.