Pauli matrices
Encyclopedia
The Pauli matrices are a set of three 2 × 2 complex
matrices
which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" (σ), they are occasionally denoted with a "tau" (τ) when used in connection with isospin
symmetries. They are:
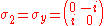
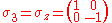
These matrices were used by, then named after, the Austrian-born physicist Wolfgang Pauli
(1900–1958), in his study of spin in quantum mechanics
.
Each Pauli matrix is Hermitian, and together with the identity I (sometimes considered the zeroth Pauli matrix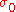
), the Pauli matrices span the full vector space of 2x2 Hermitian matrices. In the language of quantum mechanics
, hermitian matrices are observables, so the Pauli matrices span the space of observables
of the 2-dimensional complex Hilbert space
. In the context of Pauli's work,
is the observable corresponding to spin along the 
coordinate axis in 
.
The Pauli matrices (after multiplication by i to make them anti-hermitian), also generate transformations in the sense of Lie algebras
: the matrices
form a basis for 
, which exponentiates to the spin group 
, and for the identical Lie algebra 
, which exponentiates to the Lie group
of rotations of 3-dimensional space. Moreover, the algebra
generated by the four matrices
forms a faithful representation of the 3-dimensional real, Euclidean Clifford Algebra
.
where I is the identity matrix
, i.e. the matrices are involutory.
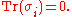
From above we can deduce that the eigenvalues of each σi are ±1.
) Pauli matrices has two eigenvalues, +1 and −1. The corresponding normalized eigenvectors are:
and provides a mapping mechanism from a vector basis to a Pauli matrix basis as follows
(summation over indices implied). Note that in this vector dotted with Pauli vector operation the Pauli matrices are treated in a scalar like fashion, commuting with the vector basis elements.
and anticommutation relations:
where
is the Levi-Civita symbol
,
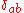is the Kronecker delta, and I is the identity matrix.
The above two relations are equivalent to:
.
For example,
and the summary equation for the commutation relations can be used to prove
as well as
for
.
in the superscript, and the matrix indices as subscripts, so that the element in row 
and column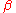 
of the 
th Pauli matrix is 
.
In this notation, the completeness relation for the Pauli matrices can be written
As noted above, it is common to denote the
unit matrix by 
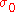, so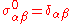 
. The completeness relation can therefore alternatively be expressed as
.
be the permutation (transposition, actually) between two spins 
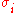and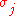 
living in the tensor product space 
, 
. This operator can be written as 
, as the reader can easily verify.
, and its Lie algebra
is the set of the anti-Hermitian 2×2 matrices with trace 0. Direct calculation shows that the Lie algebra
su(2) is the 3 dimensional real algebra spanned
by the set {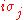
}. In symbols,
As a result,
s can be seen as infinitesimal generators of SU(2).
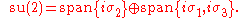
We put
and
Using the algebraic identities listed in the previous section, it can be verified that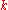
and 
form a Cartan pair
of the Lie algebra SU(2). Furthermore,
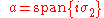
is a maximal abelian subalgebra of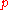
. Now, a version of Cartan decomposition
states that any element U in the Lie group SU(2) can be expressed in the form
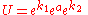where 
and 
In other words, any unitary U of determinant 1 is of the form
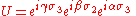
for some real numbers α, β, and γ. Physically, this corresponds to the important z-y-z
decomposition of a general 3D rotation.
Extending to unitary matrices gives that any unitary 2 × 2 U is of the form
where the additional parameter δ is also real (also compare with Leonhardt 2010, eq 5.22, pg. 99)
to the Lie algebra so(3), which corresponds to the Lie group SO(3), the group
of rotation
s in three-dimensional space. In other words, one can say that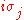
's are a realization (and, in fact, the lowest-dimensional realization) of infinitesimal rotations in three-dimensional space. However, even though su(2) and so(3) are isomorphic as Lie algebras, SU(2) and SO(3) are not isomorphic as Lie groups. SU(2) is actually a double cover of SO(3), meaning that there is a two-to-one homomorphism from SU(2) to SO(3).
is isomorphic to the real algebra of quaternions H. The isomorphism from H to this set is given by the following map (notice the reversed signs for the Pauli matrices):
Alternatively, the isomorphism can be achieved by a map using the Pauli matrices in reversed order,
As the quaternions of unit norm is group-isomorphic to SU(2), this gives yet another way of describing SU(2) via the Pauli matrices. The two-to-one homomorphism from SU(2) to SO(3) can also be explicitly given in terms of the Pauli matrices in this formulation.
Quaternions form a division algebra
—every non-zero element has an inverse—whereas Pauli matrices do not. For a quaternionic version of the algebra generated by Pauli matrices see biquaternions, which is a venerable algebra of eight real dimensions.
:
:
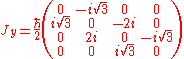
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" (σ), they are occasionally denoted with a "tau" (τ) when used in connection with isospin
Isospin
In physics, and specifically, particle physics, isospin is a quantum number related to the strong interaction. This term was derived from isotopic spin, but the term is confusing as two isotopes of a nucleus have different numbers of nucleons; in contrast, rotations of isospin maintain the number...
symmetries. They are:
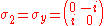
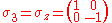
These matrices were used by, then named after, the Austrian-born physicist Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
(1900–1958), in his study of spin in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Each Pauli matrix is Hermitian, and together with the identity I (sometimes considered the zeroth Pauli matrix
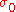), the Pauli matrices span the full vector space of 2x2 Hermitian matrices. In the language of quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, hermitian matrices are observables, so the Pauli matrices span the space of observables
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
of the 2-dimensional complex Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. In the context of Pauli's work,
is the observable corresponding to spin along the coordinate axis in .The Pauli matrices (after multiplication by i to make them anti-hermitian), also generate transformations in the sense of Lie algebras
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
: the matrices
form a basis for , which exponentiates to the spin group , and for the identical Lie algebra , which exponentiates to the Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of rotations of 3-dimensional space. Moreover, the algebraAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
generated by the four matrices
forms a faithful representation of the 3-dimensional real, Euclidean Clifford AlgebraClifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
.
Algebraic properties
where I is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, i.e. the matrices are involutory.
- The determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s and traces of the Pauli matrices are:
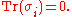
From above we can deduce that the eigenvalues of each σi are ±1.
- Together with the identity matrix I (which is sometimes written as σ0), the Pauli matrices form an orthogonal basis, in the sense of Hilbert-Schmidt, for the real Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of 2 × 2 complex Hermitian matrices, or the complex Hilbert space of all 2 × 2 matrices.
Eigenvectors and eigenvalues
Each of the (hermitianHermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
) Pauli matrices has two eigenvalues, +1 and −1. The corresponding normalized eigenvectors are:
Pauli vector
The Pauli vector is defined byand provides a mapping mechanism from a vector basis to a Pauli matrix basis as follows
(summation over indices implied). Note that in this vector dotted with Pauli vector operation the Pauli matrices are treated in a scalar like fashion, commuting with the vector basis elements.
Commutation relations
The Pauli matrices obey the following commutationCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
and anticommutation relations:
where
is the Levi-Civita symbolLevi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
,
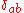is the Kronecker delta, and I is the identity matrix.The above two relations are equivalent to:
.For example,
and the summary equation for the commutation relations can be used to prove
as well as
for
.Completeness relation
An alternative notation that is commonly used for the Pauli matrices is to write the vector index in the superscript, and the matrix indices as subscripts, so that the element in row and column 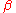of the th Pauli matrix is .In this notation, the completeness relation for the Pauli matrices can be written
As noted above, it is common to denote the
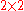unit matrix by 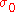, so 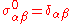. The completeness relation can therefore alternatively be expressed as.Relation with the permutation operator
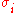Let be the permutation (transposition, actually) between two spins and 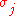living in the tensor product space , . This operator can be written as , as the reader can easily verify.SU(2)
The matrix group SU(2) is a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, and its Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is the set of the anti-Hermitian 2×2 matrices with trace 0. Direct calculation shows that the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
su(2) is the 3 dimensional real algebra spanned
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
by the set {
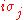}. In symbols,As a result,
s can be seen as infinitesimal generators of SU(2).A Cartan decomposition of SU(2)
This relationship between the Pauli matrices and SU(2) can be explored further, as can be seen from the following simple example. We can write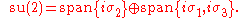We put
and
Using the algebraic identities listed in the previous section, it can be verified that
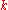and form a Cartan pairCartan decomposition
The Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition of matrices.- Cartan involutions on Lie algebras :...
of the Lie algebra SU(2). Furthermore,
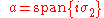
is a maximal abelian subalgebra of
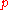. Now, a version of Cartan decompositionCartan decomposition
The Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition of matrices.- Cartan involutions on Lie algebras :...
states that any element U in the Lie group SU(2) can be expressed in the form
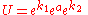where and In other words, any unitary U of determinant 1 is of the form
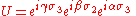
for some real numbers α, β, and γ. Physically, this corresponds to the important z-y-z
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
decomposition of a general 3D rotation.
Extending to unitary matrices gives that any unitary 2 × 2 U is of the form
where the additional parameter δ is also real (also compare with Leonhardt 2010, eq 5.22, pg. 99)
SO(3)
The Lie algebra su(2) is isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the Lie algebra so(3), which corresponds to the Lie group SO(3), the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s in three-dimensional space. In other words, one can say that
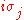's are a realization (and, in fact, the lowest-dimensional realization) of infinitesimal rotations in three-dimensional space. However, even though su(2) and so(3) are isomorphic as Lie algebras, SU(2) and SO(3) are not isomorphic as Lie groups. SU(2) is actually a double cover of SO(3), meaning that there is a two-to-one homomorphism from SU(2) to SO(3).Quaternions
The real linear span of is isomorphic to the real algebra of quaternions H. The isomorphism from H to this set is given by the following map (notice the reversed signs for the Pauli matrices):Alternatively, the isomorphism can be achieved by a map using the Pauli matrices in reversed order,
As the quaternions of unit norm is group-isomorphic to SU(2), this gives yet another way of describing SU(2) via the Pauli matrices. The two-to-one homomorphism from SU(2) to SO(3) can also be explicitly given in terms of the Pauli matrices in this formulation.
Quaternions form a division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
—every non-zero element has an inverse—whereas Pauli matrices do not. For a quaternionic version of the algebra generated by Pauli matrices see biquaternions, which is a venerable algebra of eight real dimensions.
Quantum mechanics
- In quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, each Pauli matrix is related to an operatorOperatorIn basic mathematics, an operator is a symbol or function representing a mathematical operation.In terms of vector spaces, an operator is a mapping from one vector space or module to another. Operators are of critical importance to both linear algebra and functional analysis, and they find...
that corresponds to an observableObservableIn physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
describing the spinSpin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of a spin ½Spin-½In quantum mechanics, spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.- Overview :Particles...
particle, in each of the three spatial directions. Also, as an immediate consequence of the Cartan decomposition mentioned above,
are the generators of rotation acting on non-relativisticTheory of relativityThe theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
particles with spin ½. The stateMathematical formulation of quantum mechanicsThe mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
of the particles are represented as two-component spinorSpinorIn mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s. An interesting property of spin ½ particles is that they must be rotated by an angle of 4
in order to return to their original configuration. This is due to the two-to-one correspondence between SU(2) and SO(3) mentioned above, and the fact that, although one visualizes spin up/down as the north/south pole on the 2-sphere S2, they are actually represented by orthogonal vectors in the two dimensional complex Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
.
- For a spin particle, the spin operator is given by
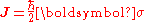. It is possible to form generalizations of the Pauli matrices in order to describe higher spin systems in three spatial dimensions. The spin matrices for spin 1 and spin 
are given below:
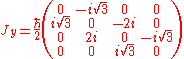
::- Also useful in the quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
of multiparticle systems, the general Pauli group Gn is defined to consist of all n-fold tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
products of Pauli matrices.
- The fact that any 2 × 2 complex Hermitian matrices can be expressed in terms of the identity matrix and the Pauli matrices also leads to the Bloch sphereBloch sphereIn quantum mechanics, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system , named after the physicist Felix Bloch....
representation of 2 × 2 mixed states (2 × 2 positive semidefinite matrices with trace 1). This can be seen by simply first writing a Hermitian matrix as a real linear combination of {σ0, σ1, σ2, σ3} then impose the positive semidefinite and traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
1 assumptions.
Quantum information
- In quantum informationQuantum informationIn quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
, single-qubitQubitIn quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
quantum gateQuantum gateIn quantum computing and specifically the quantum circuit model of computation, a quantum gate is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.Unlike many classical...
s are 2 × 2 unitary matrices. The Pauli matrices are some of the most important single-qubit operations. In that context, the Cartan decomposition given above is called the Z-Y decomposition of a single-qubit gate. Choosing a different Cartan pair gives a similar X-Y decomposition of a single-qubit gate.
See also
- Angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
- Gell-Mann matricesGell-Mann matricesThe Gell-Mann matrices, named for Murray Gell-Mann, are one possible representation of the infinitesimal generators of the special unitary group called SU....
- Generalizations of Pauli matricesGeneralizations of Pauli matricesIn mathematics and physics, in particular quantum information, the term generalized Pauli matrices refers to families of matrices which generalize the properties of the Pauli matrices. In this article we give a few classes of such matrices....
- Poincaré groupPoincaré groupIn physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
- Pauli equationPauli equationThe Pauli equation, also known as the Schrödinger–Pauli equation, is the formulation of the Schrödinger equation for spin- particles which takes into account the interaction of the particle's spin with the electromagnetic field...