Qubit
Encyclopedia
In quantum computing, a qubit (icon) or quantum bit is a unit of quantum information
—the quantum analogue of the classical bit
—with additional dimensions associated to the quantum properties
of a physical atom
.
The physical construction of a quantum computer is itself an arrangement of entangled
atoms, and the qubit represents both the state memory and the state of entanglement in a system. A quantum computation is performed by initializing
a system of qubits with a quantum algorithm
—"initialization" here referring to some advanced physical process that puts the system into an entangled state.
The qubit is described by a quantum state in a two-state quantum-mechanical system, which is formally equivalent to a two-dimensional vector space
over the complex number
s. One example of a two-state quantum system is the polarization
of a single photon
: here the two states are vertical polarization and horizontal polarization. In a classical system, a bit would have to be in one state or the other, but quantum mechanics allows the qubit to be in a superposition
of both states at the same time, a property which is fundamental to quantum computing.
is the basic unit of computer information. Regardless of its physical realization, a bit is always understood to be either a 0 or a 1. An analogy to this is a light switch— with the off position representing 0 and the on position representing 1.
A qubit has some similarities to a classical bit, but is overall very different. Like a bit, a qubit can have two possible values—normally a 0 or a 1. The difference is that whereas a bit must be either 0 or 1, a qubit can be 0, 1, or a superposition
of both.
states (or basis vector
s). As is the tradition with any sort of quantum states, Dirac, or bra-ket notation
, is used to represent them. This means that the two computational basis states are conventionally written as and
and 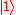 .
.
 A pure qubit state is a linear superposition
A pure qubit state is a linear superposition
of the basis states. This means that the qubit can be represented as a linear combination
of and
and 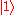 :
:
where α and β are probability amplitude
s and can in general both be complex number
s.
When we measure this qubit in the standard basis, the probability of outcome is
is 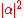 and the probability of outcome
and the probability of outcome 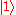 is
is 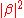 . Because the absolute squares of the amplitudes equate to probabilities, it follows that α and β must be constrained by the equation
. Because the absolute squares of the amplitudes equate to probabilities, it follows that α and β must be constrained by the equation
simply because this ensures you must measure either one state or the other.
(see diagram). Represented on such a sphere, a classical bit could only be at the "North Pole" or the "South Pole", in the locations where and
and 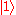 are respectively. The rest of the surface of the sphere is inaccessible to a classical bit, but a pure qubit state can be represented by any point on the surface. For example the pure qubit state
are respectively. The rest of the surface of the sphere is inaccessible to a classical bit, but a pure qubit state can be represented by any point on the surface. For example the pure qubit state 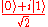 would lie on the equator of the sphere, on the positive y axis.
would lie on the equator of the sphere, on the positive y axis.
The surface of the sphere is two-dimensional space, which represents the state space
of the pure qubit states. This state space has two local degrees of freedom
. It might at first sight seem that there should be four degrees of freedom, as α and β are complex numbers with two degrees of freedom each. However, one degree of freedom is removed by the constraint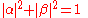 . Another, the overall phase
. Another, the overall phase
of the state, has no physically observable consequences, so we can arbitrarily choose α to be real, leaving just two degrees of freedom.
It is possible to put the qubit in a mixed state, a statistical combination of different pure states. Mixed states can be represented by points inside the Bloch sphere.
. Entanglement is a nonlocal
property that allows a set of qubits to express higher correlation than is possible in classical systems. Take, for example, two entangled qubits in the Bell state

In this state, called an equal superposition, there are equal probabilities of measuring either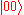 or
or 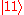 , as
, as 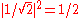 .
.
Imagine that these two entangled qubits are separated, with one each given to Alice and Bob. Alice makes a measurement of her qubit, obtaining—with equal probabilities—either or
or 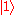 . Because of the qubits' entanglement, Bob must now get exactly the same measurement as Alice; i.e., if she measures a
. Because of the qubits' entanglement, Bob must now get exactly the same measurement as Alice; i.e., if she measures a  , Bob must measure the same, as
, Bob must measure the same, as  is the only state where Alice's qubit is a
is the only state where Alice's qubit is a  .
.
Entanglement also allows multiple states (such as the Bell state
mentioned above) to be acted on simultaneously, unlike classical bits that can only have one value at a time. Entanglement is a necessary ingredient of any quantum computation that cannot be done efficiently on a classical computer.
Many of the successes of quantum computation and communication, such as quantum teleportation
and superdense coding
, make use of entanglement, suggesting that entanglement is a resource
that is unique to quantum computation.
. Quantum computer
s perform calculations by manipulating qubits within a register. A qubyte is a collection of eight entangled
qubits. It was first demonstrated by a team at the Institute of Quantum Optics and Quantum Information at the University of Innsbruck in Austria in December 2005.
is a unit of quantum information in a 3-level quantum system. This is analogous to the unit of classical information trit. The term "qudit" is used to denote a unit of quantum information in a d-level quantum system. A quiet qubit refers to a qubit that can be efficiently decoupled from the environment.
The following is an incomplete list of physical implementations of qubits, and the choices of basis are by convention only.
, an international team of scientists that included researchers with the U.S. Department of Energy's Lawrence Berkeley National Laboratory
(Berkeley Lab) reported the first relatively long (1.75 seconds) and coherent transfer of a superposition state in an electron spin 'processing' qubit to a nuclear spin 'memory' qubit. This event can be considered the first relatively consistent quantum Data storage, a vital step towards the development of quantum computing.
in 1983, in his proposal for unforgeable quantum money
, which he had tried to publish for over a decade.
The coining of the term "qubit" is attributed to Benjamin Schumacher
. In the acknowledgments of his paper, Schumacher states that the term qubit was invented in jest (due to its phonological resemblance with an ancient unit of length called cubit
), during a conversation with William Wootters
. The paper describes a way of compressing states emitted by a quantum source of information so that they require fewer physical resources to store. This procedure is now known as Schumacher compression.
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
—the quantum analogue of the classical bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
—with additional dimensions associated to the quantum properties
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
of a physical atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
.
The physical construction of a quantum computer is itself an arrangement of entangled
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
atoms, and the qubit represents both the state memory and the state of entanglement in a system. A quantum computation is performed by initializing
Initialization (programming)
In computer programming, initialization is the assignment of an initial value for a data object or variable. The manner in which initialization is performed depends on programming language, as well as type, storage class, etc., of an object to be initialized. Programming constructs which perform...
a system of qubits with a quantum algorithm
Quantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
—"initialization" here referring to some advanced physical process that puts the system into an entangled state.
The qubit is described by a quantum state in a two-state quantum-mechanical system, which is formally equivalent to a two-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. One example of a two-state quantum system is the polarization
Photon polarization
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
of a single photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
: here the two states are vertical polarization and horizontal polarization. In a classical system, a bit would have to be in one state or the other, but quantum mechanics allows the qubit to be in a superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of both states at the same time, a property which is fundamental to quantum computing.
Bit versus qubit
A bitBit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
is the basic unit of computer information. Regardless of its physical realization, a bit is always understood to be either a 0 or a 1. An analogy to this is a light switch— with the off position representing 0 and the on position representing 1.
A qubit has some similarities to a classical bit, but is overall very different. Like a bit, a qubit can have two possible values—normally a 0 or a 1. The difference is that whereas a bit must be either 0 or 1, a qubit can be 0, 1, or a superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of both.
Representation
The two states in which a qubit may be measured are known as basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
states (or basis vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s). As is the tradition with any sort of quantum states, Dirac, or bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
, is used to represent them. This means that the two computational basis states are conventionally written as
 and
and 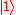 .
.Qubit states

Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of the basis states. This means that the qubit can be represented as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of
 and
and 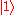 :
:where α and β are probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
s and can in general both be complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
When we measure this qubit in the standard basis, the probability of outcome
 is
is 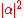 and the probability of outcome
and the probability of outcome 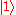 is
is 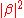 . Because the absolute squares of the amplitudes equate to probabilities, it follows that α and β must be constrained by the equation
. Because the absolute squares of the amplitudes equate to probabilities, it follows that α and β must be constrained by the equationsimply because this ensures you must measure either one state or the other.
Bloch Sphere
The possible states for a single qubit can be visualised using a Bloch sphereBloch sphere
In quantum mechanics, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system , named after the physicist Felix Bloch....
(see diagram). Represented on such a sphere, a classical bit could only be at the "North Pole" or the "South Pole", in the locations where
 and
and 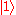 are respectively. The rest of the surface of the sphere is inaccessible to a classical bit, but a pure qubit state can be represented by any point on the surface. For example the pure qubit state
are respectively. The rest of the surface of the sphere is inaccessible to a classical bit, but a pure qubit state can be represented by any point on the surface. For example the pure qubit state 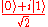 would lie on the equator of the sphere, on the positive y axis.
would lie on the equator of the sphere, on the positive y axis.The surface of the sphere is two-dimensional space, which represents the state space
State space (physics)
In physics, a state space is a complex Hilbert space within which the possible instantaneous states of the system may be described by a unit vector. These state vectors, using Dirac's bra-ket notation, can often be treated as vectors and operated on using the rules of linear algebra...
of the pure qubit states. This state space has two local degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
. It might at first sight seem that there should be four degrees of freedom, as α and β are complex numbers with two degrees of freedom each. However, one degree of freedom is removed by the constraint
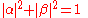 . Another, the overall phase
. Another, the overall phasePhase factor
For any complex number written in polar form , the phase factor is the exponential part, i.e. eiθ. As such, the term "phase factor" is similar to the term phasor, although the former term is more common in quantum mechanics. This phase factor is itself a complex number of absolute value 1...
of the state, has no physically observable consequences, so we can arbitrarily choose α to be real, leaving just two degrees of freedom.
It is possible to put the qubit in a mixed state, a statistical combination of different pure states. Mixed states can be represented by points inside the Bloch sphere.
Operations on pure qubit states
There are various kinds of physical operations that can be performed on pure qubit states.- A quantum logic gate can operate on a qubit: mathematically speaking, the qubit undergoes a unitary transformationUnitary transformationIn mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
. Unitary transformations correspond to rotations of the Bloch sphere. - Standard basis measurement is an operation in which information is gained about the state of the qubit. The result of the measurement will be either
 , with probability
, with probability 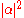 , or
, or 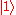 , with probability
, with probability 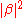 . Measurement of the state of the qubit alters the values of α and β. For instance, if the result of the measurement is
. Measurement of the state of the qubit alters the values of α and β. For instance, if the result of the measurement is  , α is changed to 1 (up to phase) and β is changed to 0. Note that a measurement of a qubit state entangled with another quantum system transforms a pure state into a mixed state.
, α is changed to 1 (up to phase) and β is changed to 0. Note that a measurement of a qubit state entangled with another quantum system transforms a pure state into a mixed state.
Entanglement
An important distinguishing feature between a qubit and a classical bit is that multiple qubits can exhibit quantum entanglementQuantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
. Entanglement is a nonlocal
Quantum nonlocality
Quantum nonlocality is the phenomenon by which measurements made at a microscopic level necessarily refute one or more notions that are regarded as intuitively true in classical mechanics...
property that allows a set of qubits to express higher correlation than is possible in classical systems. Take, for example, two entangled qubits in the Bell state
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...

In this state, called an equal superposition, there are equal probabilities of measuring either
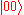 or
or 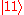 , as
, as 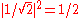 .
.Imagine that these two entangled qubits are separated, with one each given to Alice and Bob. Alice makes a measurement of her qubit, obtaining—with equal probabilities—either
 or
or 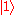 . Because of the qubits' entanglement, Bob must now get exactly the same measurement as Alice; i.e., if she measures a
. Because of the qubits' entanglement, Bob must now get exactly the same measurement as Alice; i.e., if she measures a  , Bob must measure the same, as
, Bob must measure the same, as  is the only state where Alice's qubit is a
is the only state where Alice's qubit is a  .
.Entanglement also allows multiple states (such as the Bell state
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
mentioned above) to be acted on simultaneously, unlike classical bits that can only have one value at a time. Entanglement is a necessary ingredient of any quantum computation that cannot be done efficiently on a classical computer.
Many of the successes of quantum computation and communication, such as quantum teleportation
Quantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
and superdense coding
Superdense coding
Superdense coding is a technique used in quantum information theory to send two bits of classical information using only one qubit, with the aid of entanglement.- Overview :...
, make use of entanglement, suggesting that entanglement is a resource
Computational resource
In computational complexity theory, a computational resource is a resource used by some computational models in the solution of computational problems....
that is unique to quantum computation.
Quantum register
A number of entangled qubits taken together is a qubit registerQuantum register
A quantum register is the quantum mechanical analogue of a classical processor register.A mathematical description of a quantum register is achieved by using a tensor product of qubit bra or ket vectors...
. Quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
s perform calculations by manipulating qubits within a register. A qubyte is a collection of eight entangled
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
qubits. It was first demonstrated by a team at the Institute of Quantum Optics and Quantum Information at the University of Innsbruck in Austria in December 2005.
Variations of the qubit
Similar to the qubit, a qutritQutrit
A qutrit is a unit of quantum information that can exist in three possible states.The qutrit is analogous to the classical trit, just as the qubit, a quantum particle of two possible states, is analogous to the classical bit.-Representation:...
is a unit of quantum information in a 3-level quantum system. This is analogous to the unit of classical information trit. The term "qudit" is used to denote a unit of quantum information in a d-level quantum system. A quiet qubit refers to a qubit that can be efficiently decoupled from the environment.
Physical representation
Any two-level system can be used as a qubit. Multilevel systems can be used as well, if they possess two states that can be effectively decoupled from the rest (e.g., ground state and first excited state of a nonlinear oscillator). There are various proposals. Several physical implementations which approximate two-level systems to various degrees were successfully realized. Similarly to a classical bit where the state of a transistor in a processor, the magnetization of a surface in a hard disk and the presence of current in a cable can all be used to represent bits in the same computer, an eventual quantum computer is likely to use various combinations of qubits in its design.The following is an incomplete list of physical implementations of qubits, and the choices of basis are by convention only.
| Physical support | Name | Information support |  |
 |
|---|---|---|---|---|
| Photon Photon In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force... |
Polarization encoding | Polarization of light | Horizontal | Vertical |
| Number of photons | Fock state Fock state A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:... |
Vacuum | Single photon state | |
| Time-bin encoding Time-bin encoding Time-bin encoding is a technique used in Quantum information science to encode a qubit of information on a photon. Quantum information science makes use of qubits as a basic resource similar to bits in classical computing... |
Time of arrival | Early | Late | |
| Coherent state of light | Squeezed light | Quadrature | Amplitude-squeezed state | Phase-squeezed state |
| Electron Electron The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton... s |
Electronic spin Spin quantum number In atomic physics, the spin quantum number is a quantum number that parameterizes the intrinsic angular momentum of a given particle... |
Spin | Up | Down |
| Electron number | Charge Charge (physics) In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:... |
No electron | One electron | |
| Nucleus Atomic nucleus The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The... |
Nuclear spin addressed through NMR Nuclear magnetic resonance Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation... |
Spin | Up | Down |
| Optical lattice Optical lattice An optical lattice is formed by the interference of counter-propagating laser beams, creating a spatially periodic polarization pattern. The resulting periodic potential may trap neutral atoms via the Stark shift. Atoms are cooled and congregate in the locations of potential minima... s |
Atomic spin | Spin | Up | Down |
| Josephson junction | Superconducting charge qubit Charge qubit In quantum computing, a charge qubit is a superconducting qubit whose basis states are charge states . A charge qubit is formed by a tiny superconducting island coupled by a Josephson junction to a superconducting reservoir... |
Charge | Uncharged superconducting island (Q=0) | Charged superconducting island (Q=2e, one extra Cooper pair) |
| Superconducting flux qubit Flux qubit In quantum computing, flux qubits are micrometer sized loops of superconducting metal interrupted by a number of Josephson junctions. The junction parameters are engineered during fabrication so that a persistent current will flow continuously when an external flux is applied... |
Current | Clockwise current | Counterclockwise current | |
| Superconducting phase qubit Phase qubit The phase qubit is a superconducting device based on the superconductor-insulator-superconductor Josephson junction, designed to operate as a quantum bit, or qubit. The phase qubit is closely related, yet distinct from, the flux qubit and the charge qubit, which are also quantum bits implemented... |
Energy | Ground state | First excited state | |
| Singly charged quantum dot Quantum dot A quantum dot is a portion of matter whose excitons are confined in all three spatial dimensions. Consequently, such materials have electronic properties intermediate between those of bulk semiconductors and those of discrete molecules. They were discovered at the beginning of the 1980s by Alexei... pair |
Electron localization | Charge | Electron on left dot | Electron on right dot |
| Quantum dot | Dot spin | Spin | Down | Up |
Qubit storage
In a paper entitled: "Solid-state quantum memory using the 31P nuclear spin," published in the October 23, 2008 issue of the journal NatureNature (journal)
Nature, first published on 4 November 1869, is ranked the world's most cited interdisciplinary scientific journal by the Science Edition of the 2010 Journal Citation Reports...
, an international team of scientists that included researchers with the U.S. Department of Energy's Lawrence Berkeley National Laboratory
Lawrence Berkeley National Laboratory
The Lawrence Berkeley National Laboratory , is a U.S. Department of Energy national laboratory conducting unclassified scientific research. It is located on the grounds of the University of California, Berkeley, in the Berkeley Hills above the central campus...
(Berkeley Lab) reported the first relatively long (1.75 seconds) and coherent transfer of a superposition state in an electron spin 'processing' qubit to a nuclear spin 'memory' qubit. This event can be considered the first relatively consistent quantum Data storage, a vital step towards the development of quantum computing.
Origin of the concept and term
The concept of the qubit was unknowingly introduced by Stephen WiesnerStephen Wiesner
Stephen J. Wiesner is a research physicist currently living in Israel. As a graduate student at Columbia University in New York in the late 1960s and early 1970s, he discovered several of the most important ideas in quantum information theory, including quantum money , quantum multiplexing...
in 1983, in his proposal for unforgeable quantum money
Quantum money
Quantum Money is a proposed design of bank notes making them impossible to forge, by using quantum physics. The idea influenced the development of quantum key distribution protocols used in quantum cryptography....
, which he had tried to publish for over a decade.
The coining of the term "qubit" is attributed to Benjamin Schumacher
Benjamin Schumacher
Benjamin Schumacher is a U.S. theoretical physicist, working mostly in the field of quantum information theory.He discovered a way of interpreting quantum states as information. He came up with a way of compressing the information in a state, and storing the information in a smaller number of...
. In the acknowledgments of his paper, Schumacher states that the term qubit was invented in jest (due to its phonological resemblance with an ancient unit of length called cubit
Cubit
The cubit is a traditional unit of length, based on the length of the forearm. Cubits of various lengths were employed in many parts of the world in Antiquity, in the Middle Ages and into Early Modern Times....
), during a conversation with William Wootters
William Wootters
William Kent Wootters is an American physicist, and a leading contributor to the field of quantum information theory. He proved the no cloning theorem in a joint paper with Wojciech H. Zurek. It was also independently discovered by Dennis Dieks. He has also worked on the quantification of...
. The paper describes a way of compressing states emitted by a quantum source of information so that they require fewer physical resources to store. This procedure is now known as Schumacher compression.
External links
- An update on qubits in the Oct 2005 issue of Scientific AmericanScientific AmericanScientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
- Qubit.org cofounded by one of the pioneers in quantum computation, David DeutschDavid DeutschDavid Elieser Deutsch, FRS is an Israeli-British physicist at the University of Oxford. He is a non-stipendiary Visiting Professor in the Department of Atomic and Laser Physics at the Centre for Quantum Computation in the Clarendon Laboratory of the University of Oxford...
- Quantum Computing Reading on Quantum Computing