Bell state
Encyclopedia
The Bell states are a concept in quantum information science
and represent the simplest possible examples of entanglement
. They are named after John S. Bell, as they are the subject of his famous Bell inequality
. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled with each other. Unlike classical phenomena such as the nuclear, electromagnetic, and gravitational fields, entanglement is invariant under distance of separation and is not subject to relativistic limitations such as speed of light
.
s. The qubits are usually thought to be spatially separated. Nevertheless they exhibit perfect correlation
s which cannot be explained without quantum mechanics
.
To explain, let us first look at the Bell state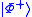
:
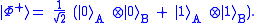
This expression means the following: The qubit held by Alice (subscript "A") can be 0 as well as 1. If Alice measured her qubit the outcome would be perfectly random, either possibility having probability 1/2. But if Bob then measured his qubit, the outcome would be the same as the one Alice got. So, if Bob measured, he would also get a random outcome on first sight, but if Alice and Bob communicated they would find out that, although the outcomes seemed random, they are correlated.
So far, this is nothing special: Maybe the two particles "agreed" in advance, when the pair was created (before the qubits were separated), which outcome they would show in case of a measurement.
Hence, followed Einstein
, Podolsky
, and Rosen
in 1935 in their famous "EPR
paper", there is something missing in the description of the qubit pair given above — namely this "agreement", called more formally a hidden variable.
But quantum mechanics allows qubits to be in quantum superposition
— i.e. in 0 and 1 simultaneously (this is misleading), e.g. in either of the states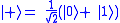
or 
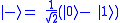. If Alice and Bob chose to measure in this basis
, i.e. check whether their qubit were
or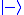 
, they will find the same correlations as above. That is because the Bell state can be formally rewritten as follows:
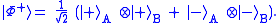
Note that this is still the same state.
John S. Bell showed in his famous paper of 1964 by using simple probability theory
arguments that these correlations cannot be perfect in case of "pre-agreement" stored in some hidden variables — but that quantum mechanics predict perfect correlations. In a more formal and refined formulation known as the Bell-CHSH inequality, this would be stated such that a certain correlation measure cannot exceed the value 2 according to reasoning assuming local "hidden variable" theory
(sort of common-sense) physics, but quantum mechanics predicts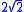
.
There are three other states of two qubits which lead to this maximal value of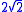
and the four are known as the four maximally entangled two-qubit states or Bell states:
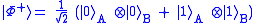
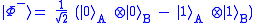
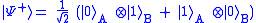
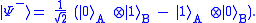
: It is a joint quantum-mechanical measurement of two qubit
s that determines in which of the four Bell states the two qubits are in.
If the qubits were not in a Bell state before, they get projected into a Bell state (according to the projection rule of quantum measurements), and as Bell states are entangled
, a Bell measurement is an entangling operation.
Bell-state measurement is the crucial step in quantum teleportation
. The result of a Bell-state measurement is used by one's co-conspirator to reconstruct the original state of a teleported particle from half of an entangled pair (the "quantum channel") that was previously shared between the two ends.
Experiments which utilize so-called "linear evolution, local measurement" techniques cannot realize a complete Bell state measurement. Linear evolution means that the detection apparatus acts on each particle independently from the state or evolution of the other, and local measurement means that each particle is localized at a particular detector registering a "click" to indicate that a particle has been detected. Such devices can be constructed, for example, from mirrors, beam splitters, and wave plates, and are attractive from an experimental perspective because they are easy to use and have a high measurement cross-section.
For entanglement in a single qubit variable, only three distinct classes out of four Bell states are distinguishable using such linear optical techniques. This means two Bell states cannot be distinguished from each other, limiting the efficiency of quantum communication protocols such as teleportation
. If a Bell state is measured from this ambiguous class, the teleportation event fails.
Entangling particles in multiple qubit variables, such as (for photonic systems) polarization and a two-element subset of orbital angular momentum
states, allows the experimenter to trace over one variable and achieve a complete Bell state measurement in the other. Leveraging so-called hyper-entangled systems thus has an advantage for teleportation. It also has advantages for other protocols such as superdense coding
, in which hyper-entanglement increases the channel capacity.
In general, for hyper-entanglement in
variables, one can distinguish between at most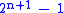 
classes out of 
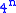Bell states using linear optical techniques.
Bell measurements of ion
qubits in ion trap
experiments, the distinction of all four states is possible.
Quantum information science
Quantum information science is an area of study based on the idea that information science depends on quantum effects in physics. It includes theoretical issues in computational models as well as more experimental topics in quantum physics including what can and cannot be done with quantum...
and represent the simplest possible examples of entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
. They are named after John S. Bell, as they are the subject of his famous Bell inequality
Bell's theorem
In theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled with each other. Unlike classical phenomena such as the nuclear, electromagnetic, and gravitational fields, entanglement is invariant under distance of separation and is not subject to relativistic limitations such as speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
The Bell states
A Bell state is defined as a maximally entangled quantum state of two qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s. The qubits are usually thought to be spatially separated. Nevertheless they exhibit perfect correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
s which cannot be explained without quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
To explain, let us first look at the Bell state
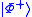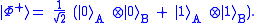
:This expression means the following: The qubit held by Alice (subscript "A") can be 0 as well as 1. If Alice measured her qubit the outcome would be perfectly random, either possibility having probability 1/2. But if Bob then measured his qubit, the outcome would be the same as the one Alice got. So, if Bob measured, he would also get a random outcome on first sight, but if Alice and Bob communicated they would find out that, although the outcomes seemed random, they are correlated.
So far, this is nothing special: Maybe the two particles "agreed" in advance, when the pair was created (before the qubits were separated), which outcome they would show in case of a measurement.
Hence, followed Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
, Podolsky
Boris Podolsky
Boris Yakovlevich Podolsky , was an American physicist of Russian Jewish descent.-Education:In 1896, Boris Podolsky was born into a poor Jewish family in Taganrog, in what was then the Russian Empire, and he moved to the United States in 1913...
, and Rosen
Nathan Rosen
Nathan Rosen was an American-Israeli physicist noted for his study on the structure of the hydrogen molecule and his work with Albert Einstein and Boris Podolsky on entangled wave functions and the EPR paradox.-Background:Nathan Rosen was born into a Jewish family in Brooklyn, New York...
in 1935 in their famous "EPR
EPR paradox
The EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...
paper", there is something missing in the description of the qubit pair given above — namely this "agreement", called more formally a hidden variable.
But quantum mechanics allows qubits to be in quantum superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
— i.e. in 0 and 1 simultaneously (this is misleading), e.g. in either of the states
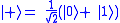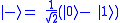or . If Alice and Bob chose to measure in this basisBasis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
, i.e. check whether their qubit were
or 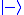, they will find the same correlations as above. That is because the Bell state can be formally rewritten as follows: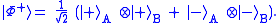Note that this is still the same state.
John S. Bell showed in his famous paper of 1964 by using simple probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
arguments that these correlations cannot be perfect in case of "pre-agreement" stored in some hidden variables — but that quantum mechanics predict perfect correlations. In a more formal and refined formulation known as the Bell-CHSH inequality, this would be stated such that a certain correlation measure cannot exceed the value 2 according to reasoning assuming local "hidden variable" theory
Local hidden variable theory
In quantum mechanics, a local hidden variable theory is one in which distant events are assumed to have no instantaneous effect on local ones....
(sort of common-sense) physics, but quantum mechanics predicts
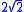.There are three other states of two qubits which lead to this maximal value of
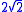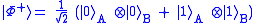
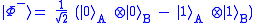
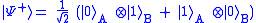
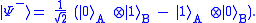
and the four are known as the four maximally entangled two-qubit states or Bell states:Bell state measurement
The Bell measurement is an important concept in quantum information scienceQuantum information science
Quantum information science is an area of study based on the idea that information science depends on quantum effects in physics. It includes theoretical issues in computational models as well as more experimental topics in quantum physics including what can and cannot be done with quantum...
: It is a joint quantum-mechanical measurement of two qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s that determines in which of the four Bell states the two qubits are in.
If the qubits were not in a Bell state before, they get projected into a Bell state (according to the projection rule of quantum measurements), and as Bell states are entangled
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
, a Bell measurement is an entangling operation.
Bell-state measurement is the crucial step in quantum teleportation
Quantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
. The result of a Bell-state measurement is used by one's co-conspirator to reconstruct the original state of a teleported particle from half of an entangled pair (the "quantum channel") that was previously shared between the two ends.
Experiments which utilize so-called "linear evolution, local measurement" techniques cannot realize a complete Bell state measurement. Linear evolution means that the detection apparatus acts on each particle independently from the state or evolution of the other, and local measurement means that each particle is localized at a particular detector registering a "click" to indicate that a particle has been detected. Such devices can be constructed, for example, from mirrors, beam splitters, and wave plates, and are attractive from an experimental perspective because they are easy to use and have a high measurement cross-section.
For entanglement in a single qubit variable, only three distinct classes out of four Bell states are distinguishable using such linear optical techniques. This means two Bell states cannot be distinguished from each other, limiting the efficiency of quantum communication protocols such as teleportation
Quantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
. If a Bell state is measured from this ambiguous class, the teleportation event fails.
Entangling particles in multiple qubit variables, such as (for photonic systems) polarization and a two-element subset of orbital angular momentum
Azimuthal quantum number
The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...
states, allows the experimenter to trace over one variable and achieve a complete Bell state measurement in the other. Leveraging so-called hyper-entangled systems thus has an advantage for teleportation. It also has advantages for other protocols such as superdense coding
Superdense coding
Superdense coding is a technique used in quantum information theory to send two bits of classical information using only one qubit, with the aid of entanglement.- Overview :...
, in which hyper-entanglement increases the channel capacity.
In general, for hyper-entanglement in
variables, one can distinguish between at most 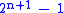classes out of 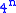Bell states using linear optical techniques.Bell measurements of ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
qubits in ion trap
Ion trap
An ion trap is a combination of electric or magnetic fields that captures ions in a region of a vacuum system or tube. Ion traps have a number of scientific uses such as mass spectrometery and trapping ions while the ion's quantum state is manipulated...
experiments, the distinction of all four states is possible.