Azimuthal quantum number
Encyclopedia
The azimuthal quantum number is a quantum number
for an atomic orbital
that determines its orbital angular momentum
and describes the shape of the orbital. The azimuthal quantum number is the second of a set of quantum numbers which describe the unique quantum state of an electron (the others being the principal quantum number
, following spectroscopic notation
, the magnetic quantum number
, and the spin quantum number
). It is also known as the orbital angular momentum quantum number or second quantum number, and is symbolized as ℓ (lower-case L).
or orbital
. The wavefunction of the Schrödinger wave equation reduces to three equations that when solved, lead to the first three quantum numbers. Therefore, the equations for the first three quantum numbers are all interrelated. The azimuthal quantum number arose in the solution of the polar part of the wave equation as shown below. To aid understanding of this concept of the azimuth, it may also prove helpful to review spherical coordinate system
s, and/or other alternative mathematical coordinate systems besides the cartesian coordinate system
. Generally, the spherical coordinate system works best with spherical models, the cylindrical system
with cylinders, the cartesian with general volumes, etc.
An atomic electron's angular momentum
, L, is related to its quantum number ℓ by the following equation:
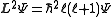
where ħ is the reduced Planck's constant, L2 is the orbital angular momentum operator and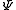
is the wavefunction of the electron. While many introductory textbooks on quantum mechanics will refer to L by itself, L has no real meaning except in its use as the angular momentum operator. When referring to angular momentum, it is best to simply use the quantum number ℓ.
The energy of any wave is the frequency multiplied by Planck's constant. This causes the wave to display particle-like packets of energy called quanta
. To show each of the quantum numbers in the quantum state, the formulae for each quantum number include Planck's reduced constant which only allows particular or discrete or quantized energy levels.
This behavior manifests itself as the "shape" of the orbital.
Atomic orbitals have distinctive shapes denoted by letters. In the illustration, the letters s, p, and d describe the shape of the atomic orbital
.
Their wavefunctions take the form of spherical harmonic
s, and so are described by Legendre polynomials
. The various orbitals relating to different values of ℓ are sometimes called sub-shells, and (mainly for historical reasons) are referred to by letters, as follows:
A mnemonic for the order of the "sub-shells" is some poor dumb fool. Another mnemonic for the order of the "sub-shells" is silly professors dance funny. The letters after the f sub-shell just follow f in alphabetical order.
Each of the different angular momentum states can take 2(2ℓ + 1) electrons. This is because the third quantum number mℓ (which can be thought of loosely as the quantized
projection of the angular momentum vector on the z-axis) runs from −ℓ to ℓ in integer units, and so there are 2ℓ + 1 possible states. Each distinct n,ℓ,mℓ orbital can be occupied by two electrons with opposing spins (given by the quantum number ms), giving 2(2ℓ + 1) electrons overall. Orbitals with higher ℓ than given in the table are perfectly permissible, but these values cover all atoms so far discovered.
For a given value of the principal quantum number
n, the possible values of ℓ range from 0 to n − 1; therefore, the n = 1 shell only possesses an s subshell and can only take 2 electrons, the n = 2 shell possesses an s and a p subshell and can take 8 electrons overall, the n = 3 shell possesses s, p and d subshells and has a maximum of 18 electrons, and so on. Generally speaking, the maximum number of electrons in the nth energy level is 2n2.
The angular momentum quantum number, ℓ, governs the number of planar nodes going through the nucleus. A planar node can be described in an electromagnetic wave as the midpoint between crest and trough, which has zero magnitude. In an s orbital, no nodes go through the nucleus, therefore the corresponding azimuthal quantum number ℓ takes the value of 0. In a p orbital, one node traverses the nucleus and therefore ℓ has the value of 1. L has the value ħ.
Depending on the value of n, there is an angular momentum quantum number ℓ and the following series. The wavelengths listed are for a hydrogen atom
:
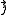which is the sum of two individual quantized angular momenta 
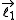and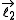 
,
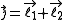
the quantum number
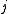associated with its magnitude can range from 
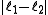to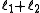 
in integer steps
where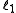
and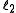 
are quantum numbers corresponding to the magnitudes of the individual angular momenta.
in the atom, the orbital angular momentum no longer commutes
with the Hamiltonian
, nor does the spin
. These therefore change over time. However the total angular momentum J does commute
with the Hamiltonian and so is constant. J is defined through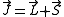
L being the orbital angular momentum and S the spin. The total angular momentum satisfies the same commutation relations as angular momentum, namely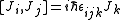
from which follows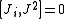
where Ji stand for Jx, Jy, and Jz.
The quantum number
s describing the system, which are constant over time, are now j and mj, defined through the action of J on the wavefunction
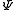
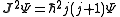
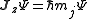
So that j is related to the norm of the total angular momentum and mj to its projection along a specified axis.
As with any angular momentum in quantum mechanics, the projection of J along other axes cannot be co-defined with Jz, because they do not commute
.
of the quantum state, replace the three quantum numbers ℓ, mℓ and ms (the projection of the spin
along the specified axis). The former quantum numbers can be related to the latter.
Furthermore, the eigenvectors of j, mj and parity, which are also eigenvectors of the Hamiltonian
, are linear combinations of the eigenvectors of ℓ, mℓ and ms.
. The Bohr model was derived from spectroscopic analysis
of the atom in combination with the Rutherford
atomic model. The lowest quantum level was found to have an angular momentum of zero. To simplify the mathematics, orbits were considered as oscillating charges in one dimension and so described as "pendulum" orbits. In three-dimensions the orbit becomes spherical without any nodes
crossing the nucleus, similar to a skipping rope that oscillates in one large circle.
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
for an atomic orbital
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
that determines its orbital angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
and describes the shape of the orbital. The azimuthal quantum number is the second of a set of quantum numbers which describe the unique quantum state of an electron (the others being the principal quantum number
Principal quantum number
In atomic physics, the principal quantum symbolized as n is the firstof a set of quantum numbers of an atomic orbital. The principal quantum number can only have positive integer values...
, following spectroscopic notation
Spectroscopic notation
Spectroscopic notation provides various ways to specify atomic ionization states, as well as atomic and molecular orbitals.-Ionization states:Spectroscopists customarily refer to the spectrum arising from a given ionization state of a given element by the element's symbol followed by a Roman numeral...
, the magnetic quantum number
Magnetic quantum number
In atomic physics, the magnetic quantum number is the third of a set of quantum numbers which describe the unique quantum state of an electron and is designated by the letter m...
, and the spin quantum number
Spin quantum number
In atomic physics, the spin quantum number is a quantum number that parameterizes the intrinsic angular momentum of a given particle...
). It is also known as the orbital angular momentum quantum number or second quantum number, and is symbolized as ℓ (lower-case L).
Derivation
Associated with the energy states of the electrons of an atom is a set of four quantum numbers: n, ℓ, mℓ, and ms. These specify the complete and unique quantum state of a single electron in an atom, and make up its wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
or orbital
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
. The wavefunction of the Schrödinger wave equation reduces to three equations that when solved, lead to the first three quantum numbers. Therefore, the equations for the first three quantum numbers are all interrelated. The azimuthal quantum number arose in the solution of the polar part of the wave equation as shown below. To aid understanding of this concept of the azimuth, it may also prove helpful to review spherical coordinate system
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
s, and/or other alternative mathematical coordinate systems besides the cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
. Generally, the spherical coordinate system works best with spherical models, the cylindrical system
Cylindrical coordinate system
A cylindrical coordinate system is a three-dimensional coordinate systemthat specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis...
with cylinders, the cartesian with general volumes, etc.
An atomic electron's angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, L, is related to its quantum number ℓ by the following equation:
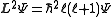
where ħ is the reduced Planck's constant, L2 is the orbital angular momentum operator and
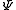is the wavefunction of the electron. While many introductory textbooks on quantum mechanics will refer to L by itself, L has no real meaning except in its use as the angular momentum operator. When referring to angular momentum, it is best to simply use the quantum number ℓ.The energy of any wave is the frequency multiplied by Planck's constant. This causes the wave to display particle-like packets of energy called quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
. To show each of the quantum numbers in the quantum state, the formulae for each quantum number include Planck's reduced constant which only allows particular or discrete or quantized energy levels.
This behavior manifests itself as the "shape" of the orbital.
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
.
Their wavefunctions take the form of spherical harmonic
Spherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
s, and so are described by Legendre polynomials
Associated Legendre polynomials
In mathematics, the associated Legendre polynomials are the canonical solutions of the general Legendre equation\,y -2xy' + \left\,y = 0,\,or equivalently...
. The various orbitals relating to different values of ℓ are sometimes called sub-shells, and (mainly for historical reasons) are referred to by letters, as follows:
| ℓ | Letter | Max electrons | Shape | Name |
|---|---|---|---|---|
| 0 | s | 2 | sphere Sphere A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point... |
sharp |
| 1 | p | 6 | two dumbbell Dumbbell The dumbbell, a type of free weight, is a piece of equipment used in weight training. It can be used individually or in pairs .-History:... s |
principal |
| 2 | d | 10 | four dumbbells or unique shape one | diffuse |
| 3 | f | 14 | eight dumbbells or unique shape two | fundamental |
| 4 | g | 18 | ||
| 5 | h | 22 | ||
| 6 | i | 26 |
A mnemonic for the order of the "sub-shells" is some poor dumb fool. Another mnemonic for the order of the "sub-shells" is silly professors dance funny. The letters after the f sub-shell just follow f in alphabetical order.
Each of the different angular momentum states can take 2(2ℓ + 1) electrons. This is because the third quantum number mℓ (which can be thought of loosely as the quantized
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
projection of the angular momentum vector on the z-axis) runs from −ℓ to ℓ in integer units, and so there are 2ℓ + 1 possible states. Each distinct n,ℓ,mℓ orbital can be occupied by two electrons with opposing spins (given by the quantum number ms), giving 2(2ℓ + 1) electrons overall. Orbitals with higher ℓ than given in the table are perfectly permissible, but these values cover all atoms so far discovered.
For a given value of the principal quantum number
Principal quantum number
In atomic physics, the principal quantum symbolized as n is the firstof a set of quantum numbers of an atomic orbital. The principal quantum number can only have positive integer values...
n, the possible values of ℓ range from 0 to n − 1; therefore, the n = 1 shell only possesses an s subshell and can only take 2 electrons, the n = 2 shell possesses an s and a p subshell and can take 8 electrons overall, the n = 3 shell possesses s, p and d subshells and has a maximum of 18 electrons, and so on. Generally speaking, the maximum number of electrons in the nth energy level is 2n2.
The angular momentum quantum number, ℓ, governs the number of planar nodes going through the nucleus. A planar node can be described in an electromagnetic wave as the midpoint between crest and trough, which has zero magnitude. In an s orbital, no nodes go through the nucleus, therefore the corresponding azimuthal quantum number ℓ takes the value of 0. In a p orbital, one node traverses the nucleus and therefore ℓ has the value of 1. L has the value ħ.
Depending on the value of n, there is an angular momentum quantum number ℓ and the following series. The wavelengths listed are for a hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
:
- n = 1, L = 0, Lyman seriesLyman seriesIn physics and chemistry, the Lyman series is the series of transitions and resulting ultraviolet emission lines of the hydrogen atom as an electron goes from n ≥ 2 to n = 1...
(ultraviolet) - n = 2, L = √2ħ, Balmer seriesBalmer seriesThe Balmer series or Balmer lines in atomic physics, is the designation of one of a set of six different named series describing the spectral line emissions of the hydrogen atom....
(visible) - n = 3, L = √6ħ, Ritz-Paschen series (short wave infrared)
- n = 5, L = 2√5ħ, Pfund series (long wave infrared).
Addition of quantized angular momenta
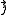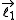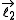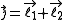
Given a quantized total angular momentum which is the sum of two individual quantized angular momenta and ,the quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
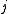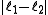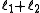associated with its magnitude can range from to in integer stepswhere
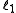and 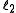are quantum numbers corresponding to the magnitudes of the individual angular momenta.Total angular momentum of an electron in the atom
Due to the spin-orbit interactionSpin-orbit interaction
In quantum physics, the spin-orbit interaction is any interaction of a particle's spin with its motion. The first and best known example of this is that spin-orbit interaction causes shifts in an electron's atomic energy levels due to electromagnetic interaction between the electron's spin and...
in the atom, the orbital angular momentum no longer commutes
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
with the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
, nor does the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
. These therefore change over time. However the total angular momentum J does commute
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
with the Hamiltonian and so is constant. J is defined through
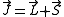
L being the orbital angular momentum and S the spin. The total angular momentum satisfies the same commutation relations as angular momentum, namely
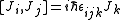
from which follows
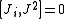
where Ji stand for Jx, Jy, and Jz.
The quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s describing the system, which are constant over time, are now j and mj, defined through the action of J on the wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
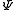
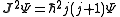
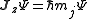
So that j is related to the norm of the total angular momentum and mj to its projection along a specified axis.
As with any angular momentum in quantum mechanics, the projection of J along other axes cannot be co-defined with Jz, because they do not commute
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
.
Relation between new and old quantum numbers
j and mj, together with the parityParity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
of the quantum state, replace the three quantum numbers ℓ, mℓ and ms (the projection of the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
along the specified axis). The former quantum numbers can be related to the latter.
Furthermore, the eigenvectors of j, mj and parity, which are also eigenvectors of the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
, are linear combinations of the eigenvectors of ℓ, mℓ and ms.
List of angular momentum quantum numbers
- Intrinsic (or spin) angular momentum quantum number, or simply spin quantum numberSpin quantum numberIn atomic physics, the spin quantum number is a quantum number that parameterizes the intrinsic angular momentum of a given particle...
- orbital angular momentum quantum number (the subject of this article)
- magnetic quantum numberMagnetic quantum numberIn atomic physics, the magnetic quantum number is the third of a set of quantum numbers which describe the unique quantum state of an electron and is designated by the letter m...
, related to the orbital momentum quantum number - total angular momentum quantum number
History
The azimuthal quantum number was carried over from the Bohr model of the atom, and was posited by Arnold SommerfeldArnold Sommerfeld
Arnold Johannes Wilhelm Sommerfeld was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and groomed a large number of students for the new era of theoretical physics...
. The Bohr model was derived from spectroscopic analysis
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
of the atom in combination with the Rutherford
Ernest Rutherford
Ernest Rutherford, 1st Baron Rutherford of Nelson OM, FRS was a New Zealand-born British chemist and physicist who became known as the father of nuclear physics...
atomic model. The lowest quantum level was found to have an angular momentum of zero. To simplify the mathematics, orbits were considered as oscillating charges in one dimension and so described as "pendulum" orbits. In three-dimensions the orbit becomes spherical without any nodes
Node (physics)
A node is a point along a standing wave where the wave has minimal amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effective length of the vibrating string and thereby the...
crossing the nucleus, similar to a skipping rope that oscillates in one large circle.
See also
- Angular momentum operatorAngular momentum operatorIn quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...
- Basic quantum mechanics
- Particle in a spherically symmetric potential
- Quantum numberQuantum numberQuantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
- Magnetic quantum numberMagnetic quantum numberIn atomic physics, the magnetic quantum number is the third of a set of quantum numbers which describe the unique quantum state of an electron and is designated by the letter m...
- Principal quantum numberPrincipal quantum numberIn atomic physics, the principal quantum symbolized as n is the firstof a set of quantum numbers of an atomic orbital. The principal quantum number can only have positive integer values...
- Spin quantum numberSpin quantum numberIn atomic physics, the spin quantum number is a quantum number that parameterizes the intrinsic angular momentum of a given particle...
- Total angular momentum quantum number
- Magnetic quantum number