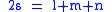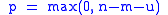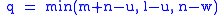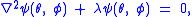Associated Legendre polynomials
Encyclopedia
In mathematics
, the associated Legendre polynomials are the canonical solutions of the general Legendre equation
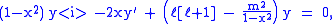
or equivalently
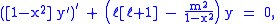
where the indices ℓ and m (which are integers) are referred to as the degree and order of the associated Legendre polynomial respectively. This equation has nonzero solutions that are nonsingular on [−1, 1] only if ℓ and m are integers with 0 ≤ m ≤ ℓ, or with trivially equivalent negative values. When in addition m is even, the function is a polynomial
. When m is zero and ℓ integer, these functions are identical to the Legendre polynomials. In general, when ℓ and m are integers, the regular solutions are sometimes called "associated Legendre polynomials", even though they are not polynomial
s when m is odd. The fully general class of functions with arbitrary real or complex values of ℓ and m are Legendre function
s. In that case the parameters are usually labelled with Greek letters.
The Legendre ordinary differential equation
is frequently encountered in physics
and other technical fields. In particular, it occurs when solving Laplace's equation
(and related partial differential equation
s) in spherical coordinates. Associated Legendre polynomials play a vital role in the definition of spherical harmonics
.
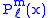 , where the superscript indicates the order, and not a power of P. Their most straightforward definition is in terms
, where the superscript indicates the order, and not a power of P. Their most straightforward definition is in terms
of derivatives of ordinary Legendre polynomials (m ≥ 0)
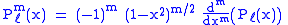
The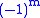 factor in this formula is known as the Condon–Shortley phase. Some authors omit it. That the functions described by this equation satisfy the general Legendre differential equation with the indicated values of the parameters ℓ and m follows by differentiating m times the Legendre equation for Pℓ:
factor in this formula is known as the Condon–Shortley phase. Some authors omit it. That the functions described by this equation satisfy the general Legendre differential equation with the indicated values of the parameters ℓ and m follows by differentiating m times the Legendre equation for Pℓ: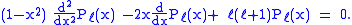
Moreover, since by Rodrigues' formula
,
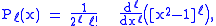
the P can be expressed in the form
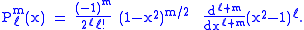
This equation allows extension of the range of m to: −ℓ ≤ m ≤ ℓ. The definitions of Pℓ±m, resulting from this expression by substitution of ±m, are proportional. Indeed,
equate the coefficients of equal powers on the left and right hand side of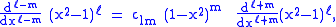
then it follows that the proportionality constant is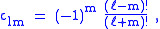
so that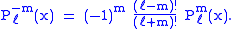
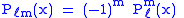
 , they satisfy the orthogonality condition for fixed m:
, they satisfy the orthogonality condition for fixed m:
Where is the Kronecker delta.
is the Kronecker delta.
Also, they satisfy the orthogonality condition for fixed ℓ:
The functions for negative m were shown above to be proportional to those of positive m:
(This followed from the Rodrigues' formula definition. This definition also makes the various recurrence formulas work for positive or negative m.)
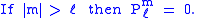
The differential equation is also invariant under a change from ℓ to
 , and the functions for negative ℓ are defined by
, and the functions for negative ℓ are defined by
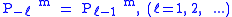 .
.
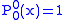
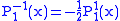
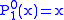
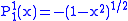

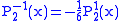
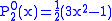
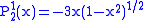
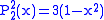
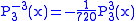
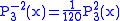
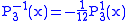

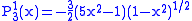
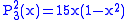
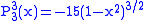
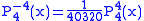
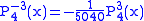
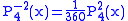
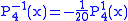

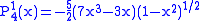
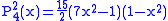
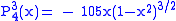
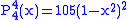
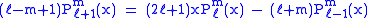
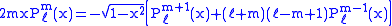

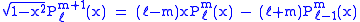

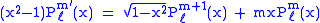
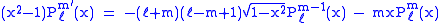
Helpful identities (initial values for the first recursion):
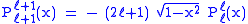
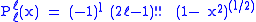
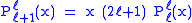
with !! the double factorial.
This formula is to be used under the following assumptions:
Other quantities appearing in the formula are defined as
The integral is zero unless
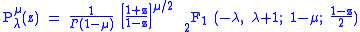
where is the gamma function
is the gamma function
and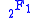 is the hypergeometric function
is the hypergeometric function
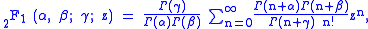
They are called the Legendre functions when defined in this more general way. They satisfy
the same differential equation as before:
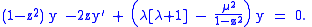
Since this is a second order differential equation, it has a second solution,
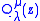 , defined as:
, defined as:
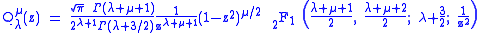
 and
and 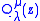 both obey the various
both obey the various
recurrence formulas given previously.
letting :
:
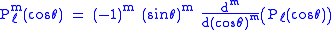
The first few polynomials, parameterized this way, are:

For fixed m,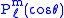 are orthogonal, parameterized by θ over
are orthogonal, parameterized by θ over 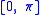 , with weight
, with weight 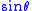 :
:

Also, for fixed ℓ:
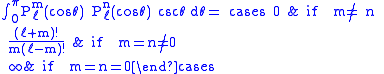
In terms of θ,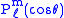 are solutions of
are solutions of
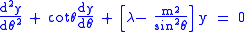
More precisely, given an integer m 0, the above equation has
0, the above equation has
nonsingular solutions only when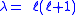 for ℓ
for ℓ
an integer ≥ m, and those solutions are proportional to
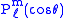 .
.
, associated Legendre polynomials in terms of angles occur where spherical symmetry
is involved. The colatitude angle in spherical coordinates is
the angle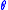 used above. The longitude angle,
used above. The longitude angle,  , appears in a multiplying factor. Together, they make a set of functions called spherical harmonic
, appears in a multiplying factor. Together, they make a set of functions called spherical harmonic
s. These functions express the symmetry of the two-sphere
under the action of the Lie group
SO(3).
What makes these functions useful is that they are central to the solution of the equation
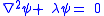 on the surface of a sphere. In spherical coordinates θ (colatitude) and φ (longitude), the Laplacian is
on the surface of a sphere. In spherical coordinates θ (colatitude) and φ (longitude), the Laplacian is

When the partial differential equation
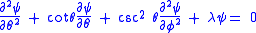
is solved by the method of separation of variables, one gets a φ-dependent part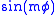 or
or 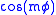 for integer m≥0, and an equation for the θ-dependent part
for integer m≥0, and an equation for the θ-dependent part
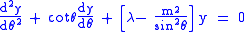
for which the solutions are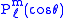 with
with 
and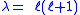 .
.
Therefore, the equation

has nonsingular separated solutions only when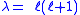 ,
,
and those solutions are proportional to
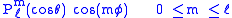
and
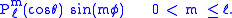
For each choice of ℓ, there are functions
for the various values of m and choices of sine and cosine.
They are all orthogonal in both ℓ and m when integrated over the
surface of the sphere.
The solutions are usually written in terms of complex exponentials:

The functions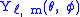 are the spherical harmonics
are the spherical harmonics
, and the quantity in the square root is a normalizing factor.
Recalling the relation between the associated Legendre functions of positive and negative m, it is easily shown that the spherical harmonics satisfy the identity
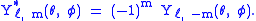
The spherical harmonic functions form a complete orthonormal set of functions in the sense of Fourier series
. It should be noted that workers in the fields of geodesy, geomagnetism and spectral analysis use a different phase and normalization factor than given here (see spherical harmonics
).
When a 3-dimensional spherically symmetric partial differential equation is solved by the method of separation of variables in spherical coordinates, the part that remains after removal of the radial part is typically
of the form
and hence the solutions are spherical harmonics.
. In the form of spherical harmonics, they express the symmetry of the two-sphere
under the action of the Lie group
SO(3). There are many other Lie groups besides SO(3), and an analogous generalization of the Legendre polynomials exist to express the symmetries of semi-simple Lie groups and Riemannian symmetric space
s. Crudely speaking, one may define a Laplacian on symmetric spaces; the eigenfunctions of the Laplacian can be thought of as generalizations of the spherical harmonics to other settings.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the associated Legendre polynomials are the canonical solutions of the general Legendre equation
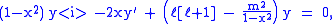
or equivalently
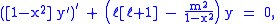
where the indices ℓ and m (which are integers) are referred to as the degree and order of the associated Legendre polynomial respectively. This equation has nonzero solutions that are nonsingular on [−1, 1] only if ℓ and m are integers with 0 ≤ m ≤ ℓ, or with trivially equivalent negative values. When in addition m is even, the function is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
. When m is zero and ℓ integer, these functions are identical to the Legendre polynomials. In general, when ℓ and m are integers, the regular solutions are sometimes called "associated Legendre polynomials", even though they are not polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s when m is odd. The fully general class of functions with arbitrary real or complex values of ℓ and m are Legendre function
Legendre function
In mathematics, the Legendre functions Pλ, Qλ and associated Legendre functions P, Q are generalizations of Legendre polynomials to non-integer degree.-Differential equation:...
s. In that case the parameters are usually labelled with Greek letters.
The Legendre ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
is frequently encountered in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and other technical fields. In particular, it occurs when solving Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
(and related partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s) in spherical coordinates. Associated Legendre polynomials play a vital role in the definition of spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
.
Definition for non-negative integer parameters ℓ and m
These functions are denoted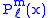 , where the superscript indicates the order, and not a power of P. Their most straightforward definition is in terms
, where the superscript indicates the order, and not a power of P. Their most straightforward definition is in termsof derivatives of ordinary Legendre polynomials (m ≥ 0)
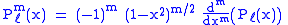
The
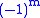 factor in this formula is known as the Condon–Shortley phase. Some authors omit it. That the functions described by this equation satisfy the general Legendre differential equation with the indicated values of the parameters ℓ and m follows by differentiating m times the Legendre equation for Pℓ:
factor in this formula is known as the Condon–Shortley phase. Some authors omit it. That the functions described by this equation satisfy the general Legendre differential equation with the indicated values of the parameters ℓ and m follows by differentiating m times the Legendre equation for Pℓ: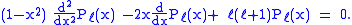
Moreover, since by Rodrigues' formula
Rodrigues' formula
In mathematics, Rodrigues's formula is a formula for Legendre polynomials independently introduced by , and...
,
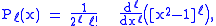
the P can be expressed in the form
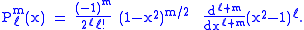
This equation allows extension of the range of m to: −ℓ ≤ m ≤ ℓ. The definitions of Pℓ±m, resulting from this expression by substitution of ±m, are proportional. Indeed,
equate the coefficients of equal powers on the left and right hand side of
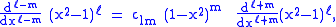
then it follows that the proportionality constant is
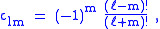
so that
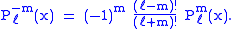
Alternative notations
The following alternative notations are also used in literature: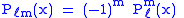
Orthogonality
Assuming , they satisfy the orthogonality condition for fixed m:
, they satisfy the orthogonality condition for fixed m: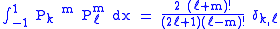
Where
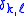 is the Kronecker delta.
is the Kronecker delta.Also, they satisfy the orthogonality condition for fixed ℓ:
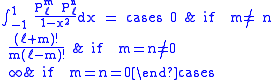
Negative m and/or negative ℓ
The differential equation is clearly invariant under a change in sign of m.The functions for negative m were shown above to be proportional to those of positive m:
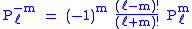
(This followed from the Rodrigues' formula definition. This definition also makes the various recurrence formulas work for positive or negative m.)
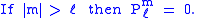
The differential equation is also invariant under a change from ℓ to
 , and the functions for negative ℓ are defined by
, and the functions for negative ℓ are defined by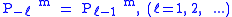 .
.The first few associated Legendre functions
The first few associated Legendre functions, including those for negative values of m, are: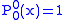
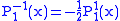
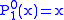
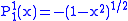

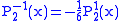
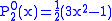
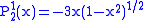
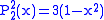
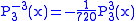
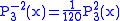
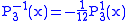

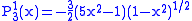
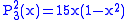
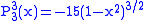
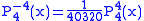
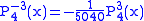
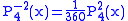
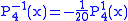

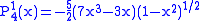
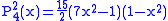
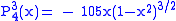
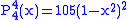
Recurrence formula
These functions have a number of recurrence properties: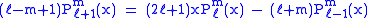
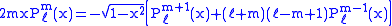

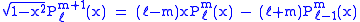

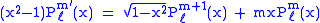
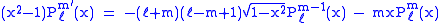
Helpful identities (initial values for the first recursion):
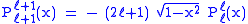
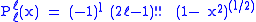
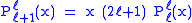
with !! the double factorial.
Gaunt's formula
The integral over the product of three associated Legendre polynomials (with orders matching as shown below) is a necessary ingredient when developing products of Legendre polynomials into a series linear in the Legendre polynomials. For instance, this turns out to be necessary when doing atomic calculations of the Hartree–Fock variety where matrix elements of the Coulomb operator are needed. For this we have Gaunt's formula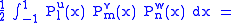 |
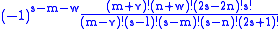 |
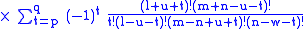 |
This formula is to be used under the following assumptions:
- the degrees are non-negative integers
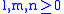
- all three orders are non-negative integers

-
 is the largest of the three orders
is the largest of the three orders - the orders sum up

- the degrees obey

Other quantities appearing in the formula are defined as
The integral is zero unless
- the sum of degrees is even so that
 is an integer
is an integer - the triangular condition is satisfied
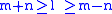
Generalization via hypergeometric functions
These functions may actually be defined for general complex parameters and argument: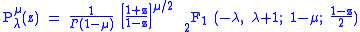
where
 is the gamma function
is the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
and
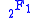 is the hypergeometric function
is the hypergeometric function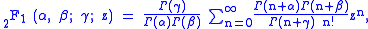
They are called the Legendre functions when defined in this more general way. They satisfy
the same differential equation as before:
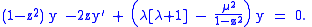
Since this is a second order differential equation, it has a second solution,
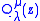 , defined as:
, defined as: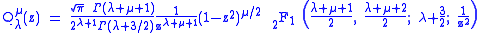
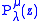 and
and 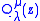 both obey the various
both obey the variousrecurrence formulas given previously.
Reparameterization in terms of angles
These functions are most useful when the argument is reparameterized in terms of angles,letting
 :
: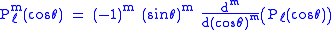
The first few polynomials, parameterized this way, are:

For fixed m,
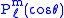 are orthogonal, parameterized by θ over
are orthogonal, parameterized by θ over 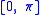 , with weight
, with weight 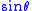 :
:
Also, for fixed ℓ:
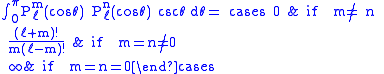
In terms of θ,
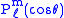 are solutions of
are solutions of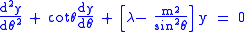
More precisely, given an integer m
 0, the above equation has
0, the above equation hasnonsingular solutions only when
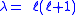 for ℓ
for ℓan integer ≥ m, and those solutions are proportional to
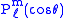 .
.Applications in physics: spherical harmonics
In many occasions in physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, associated Legendre polynomials in terms of angles occur where spherical symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
is involved. The colatitude angle in spherical coordinates is
the angle
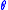 used above. The longitude angle,
used above. The longitude angle,  , appears in a multiplying factor. Together, they make a set of functions called spherical harmonic
, appears in a multiplying factor. Together, they make a set of functions called spherical harmonicSpherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
s. These functions express the symmetry of the two-sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
under the action of the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
SO(3).
What makes these functions useful is that they are central to the solution of the equation
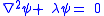 on the surface of a sphere. In spherical coordinates θ (colatitude) and φ (longitude), the Laplacian is
on the surface of a sphere. In spherical coordinates θ (colatitude) and φ (longitude), the Laplacian is
When the partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
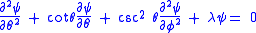
is solved by the method of separation of variables, one gets a φ-dependent part
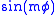 or
or 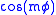 for integer m≥0, and an equation for the θ-dependent part
for integer m≥0, and an equation for the θ-dependent part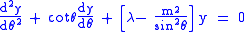
for which the solutions are
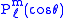 with
with 
and
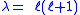 .
.Therefore, the equation

has nonsingular separated solutions only when
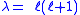 ,
,and those solutions are proportional to
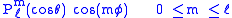
and
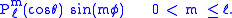
For each choice of ℓ, there are functions
for the various values of m and choices of sine and cosine.
They are all orthogonal in both ℓ and m when integrated over the
surface of the sphere.
The solutions are usually written in terms of complex exponentials:

The functions
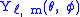 are the spherical harmonics
are the spherical harmonicsSpherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
, and the quantity in the square root is a normalizing factor.
Recalling the relation between the associated Legendre functions of positive and negative m, it is easily shown that the spherical harmonics satisfy the identity
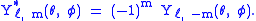
The spherical harmonic functions form a complete orthonormal set of functions in the sense of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. It should be noted that workers in the fields of geodesy, geomagnetism and spectral analysis use a different phase and normalization factor than given here (see spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
).
When a 3-dimensional spherically symmetric partial differential equation is solved by the method of separation of variables in spherical coordinates, the part that remains after removal of the radial part is typically
of the form
and hence the solutions are spherical harmonics.
Generalizations
The Legendre polynomials are closely related to hypergeometric seriesHypergeometric series
In mathematics, a generalized hypergeometric series is a series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by...
. In the form of spherical harmonics, they express the symmetry of the two-sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
under the action of the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
SO(3). There are many other Lie groups besides SO(3), and an analogous generalization of the Legendre polynomials exist to express the symmetries of semi-simple Lie groups and Riemannian symmetric space
Riemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
s. Crudely speaking, one may define a Laplacian on symmetric spaces; the eigenfunctions of the Laplacian can be thought of as generalizations of the spherical harmonics to other settings.
See also
- Angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
- Gaussian quadratureGaussian quadratureIn numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....
- Legendre polynomials
- Spherical harmonicSpherical HarmonicSpherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
s - Whipple's transformation of Legendre functions