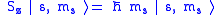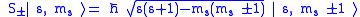Spin quantum number
Encyclopedia
In atomic physics
, the spin quantum number is a quantum number
that parameterizes the intrinsic angular momentum
(or spin angular momentum, or simply spin
) of a given particle
. The spin quantum number is the fourth of a set of quantum number
s (the principal quantum number
, the azimuthal quantum number
, the magnetic quantum number
, and the spin quantum number), which describe the unique quantum state of an electron and is designated by the letter s.
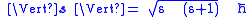
where
Given an arbitrary direction z (usually determined by an external magnetic field) the spin z-projection is given by
where ms is the secondary spin quantum number, ranging from −s to +s in steps of one. This generates 2s+1 different values of ms.
The allowed values for s are non-negative integer
s or half-integer
s. Fermion
s (such as the electron
, proton
or neutron
) have half-integer values, whereas boson
s (e.g., photon
, meson
s) have integer spin values.
First of all, spin satisfies the fundamental commutation relation: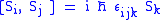 ,
, 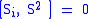
where εlmn is the (antisymmetric) Levi-Civita symbol
. This means that it is impossible to know two coordinates of the spin at the same time because of the restriction of the Uncertainty principle
.
Next, the eigenvectors of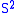 and
and 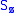 satisfy:
satisfy:
where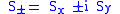 are the creation and annihilation (or "raising" and "lowering" or "up" and "down") operators.
are the creation and annihilation (or "raising" and "lowering" or "up" and "down") operators.
for the hydrogen atom
, the simplest possible case, with a single electron bound to the atomic nucleus
. This was successful in explaining many features of atomic spectra
.
The solutions required each possible state of the electron
to be described by three "quantum numbers", n, l, and m. These were identified as, respectively, the electron "shell" number, n, the "orbital" number, l, and the "orbital angular momentum" number m. Angular momentum
is a so- called "classical" concept measuring the momentum
of a mass in circular motion about a point. The shell numbers start at 1 and increase indefinitely. Each shell of number n contains n² orbitals. Each orbital is characterized by its number l, where l takes integer values from 0 to n−1, and its angular momentum number m, where m takes integer values from +l to −l. By means of a variety of approximations and extensions, physicists were able to extend their work on hydrogen to more complex atoms containing many electrons.
Atomic spectra
measure radiation absorbed or emitted by electrons "jumping"
from one "state" to another, where a state is represented by values of n, l, and m. The so-called "Transition rule" limits what "jumps" are possible. In general, a jump or "transition" is allowed only if all three numbers change in the process. This is because a transition will be able to cause the emission or absorption of electromagnetic radiation only if it involves a change in the electromagnetic dipole
of the atom.
However, it was recognized in the early years of quantum mechanics that atomic spectra
measured in an external magnetic field (see Zeeman effect
) cannot be predicted with just n, l, and m. A solution to this problem was suggested in early 1925
by George Uhlenbeck and Samuel Goudsmit, students of Paul Ehrenfest
(who rejected the idea), and independently by Ralph Kronig
, one of Landé
's assistants. Uhlenbeck, Goudsmit, and Kronig introduced the idea of the self-rotation of the electron, which would naturally give rise to an angular momentum vector in addition to the one associated with orbital motion (quantum numbers l and m).
The spin angular momentum is characterized by a quantum number; s = 1/2
specifically for electrons. In a way analogous to other quantized angular momenta, L, it is possible to obtain an expression for the total spin angular momentum:
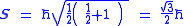
where
The hydrogen spectra fine structure is observed as a doublet corresponding to two possibilities for the z-component of the angular momentum, where for any given direction z:
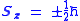
whose solution has only two possible z components for the electron. In the electron, the two different spin orientations are sometimes called "spin-up" or "spin-down".
The spin property of an electron would give rise to magnetic moment
, which was a requisite for the fourth quantum number. The electron spin magnetic moment is given by the formula:
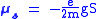
where
and by the equation:
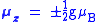
where
When atoms have even numbers of electrons the spin of each electron in each orbital has opposing orientation to that of its immediate neighbor(s). However, many atoms have an odd number of electrons or an arrangement of electrons in which there is an unequal number of "spin-up" and "spin-down" orientations. These atoms or electrons are said to have unpaired spins that are detected in electron spin resonance.
.
needed to be proved experimentally. In 1920
(two years before the theoretical description of the spin was created) Otto Stern
and Walter Gerlach
observed it in the experiment they conducted.
's model. The problem was not that a rotating charged particle would have given rise to a magnetic field but that the electron was so small that the equatorial speed of the electron would have to be greater than the speed of light for the magnetic moment to be of the observed strength.
In 1930, Paul Dirac
developed a new version of the Schrödinger Wave Equation which was relativistically invariant
, and predicted the magnetic moment correctly, and at the same time treated the electron as a point particle. In the Dirac equation
all four quantum numbers including the additional quantum number, s arose naturally during its solution.
Atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
, the spin quantum number is a quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
that parameterizes the intrinsic angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
(or spin angular momentum, or simply spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
) of a given particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
. The spin quantum number is the fourth of a set of quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s (the principal quantum number
Principal quantum number
In atomic physics, the principal quantum symbolized as n is the firstof a set of quantum numbers of an atomic orbital. The principal quantum number can only have positive integer values...
, the azimuthal quantum number
Azimuthal quantum number
The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...
, the magnetic quantum number
Magnetic quantum number
In atomic physics, the magnetic quantum number is the third of a set of quantum numbers which describe the unique quantum state of an electron and is designated by the letter m...
, and the spin quantum number), which describe the unique quantum state of an electron and is designated by the letter s.
Derivation
As a quantized angular momentum, (see angular momentum quantum number) it holds that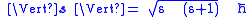
where
-
 is the quantized spin vector
is the quantized spin vector -
 is the normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
is the normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of the spin vector -
 is the spin quantum number associated with the spin angular momentum
is the spin quantum number associated with the spin angular momentum -
 is the reduced Planck constant.
is the reduced Planck constant.
Given an arbitrary direction z (usually determined by an external magnetic field) the spin z-projection is given by

where ms is the secondary spin quantum number, ranging from −s to +s in steps of one. This generates 2s+1 different values of ms.
The allowed values for s are non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s or half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
s. Fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s (such as the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
or neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
) have half-integer values, whereas boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s (e.g., photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
, meson
Meson
In particle physics, mesons are subatomic particles composed of one quark and one antiquark, bound together by the strong interaction. Because mesons are composed of sub-particles, they have a physical size, with a radius roughly one femtometer: 10−15 m, which is about the size of a proton...
s) have integer spin values.
Algebra
The algebraic theory of spin is a carbon copy of the Angular momentum in quantum mechanics theory.First of all, spin satisfies the fundamental commutation relation:
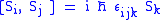 ,
, 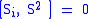
where εlmn is the (antisymmetric) Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
. This means that it is impossible to know two coordinates of the spin at the same time because of the restriction of the Uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
.
Next, the eigenvectors of
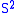 and
and 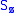 satisfy:
satisfy:
where
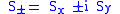 are the creation and annihilation (or "raising" and "lowering" or "up" and "down") operators.
are the creation and annihilation (or "raising" and "lowering" or "up" and "down") operators.Electron spin
Early attempts to explain the behavior of electrons in atoms focused on solving the Schrödinger wave equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for the hydrogen atom
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
, the simplest possible case, with a single electron bound to the atomic nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
. This was successful in explaining many features of atomic spectra
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
.
The solutions required each possible state of the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
to be described by three "quantum numbers", n, l, and m. These were identified as, respectively, the electron "shell" number, n, the "orbital" number, l, and the "orbital angular momentum" number m. Angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
is a so- called "classical" concept measuring the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
of a mass in circular motion about a point. The shell numbers start at 1 and increase indefinitely. Each shell of number n contains n² orbitals. Each orbital is characterized by its number l, where l takes integer values from 0 to n−1, and its angular momentum number m, where m takes integer values from +l to −l. By means of a variety of approximations and extensions, physicists were able to extend their work on hydrogen to more complex atoms containing many electrons.
Atomic spectra
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
measure radiation absorbed or emitted by electrons "jumping"
Quantum leap
In physics and chemistry, an atomic electron transition is a change of an electron from one quantum state to another within an atom...
from one "state" to another, where a state is represented by values of n, l, and m. The so-called "Transition rule" limits what "jumps" are possible. In general, a jump or "transition" is allowed only if all three numbers change in the process. This is because a transition will be able to cause the emission or absorption of electromagnetic radiation only if it involves a change in the electromagnetic dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
of the atom.
However, it was recognized in the early years of quantum mechanics that atomic spectra
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
measured in an external magnetic field (see Zeeman effect
Zeeman effect
The Zeeman effect is the splitting of a spectral line into several components in the presence of a static magnetic field. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field...
) cannot be predicted with just n, l, and m. A solution to this problem was suggested in early 1925
1925 in science
The year 1925 in science and technology involved some significant events, listed below.-Biology:* July 21 - Scopes Trial: In Dayton, Tennessee, high school biology teacher John T...
by George Uhlenbeck and Samuel Goudsmit, students of Paul Ehrenfest
Paul Ehrenfest
Paul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...
(who rejected the idea), and independently by Ralph Kronig
Ralph Kronig
Ralph Kronig was a German-American physicist . He is noted for the discovery of particle spin and for his theory of x-ray absorption spectroscopy...
, one of Landé
Alfred Landé
Alfred Landé was a German-American physicist known for his contributions to quantum theory. He is responsible for the Landé g-factor an explanation of the Zeeman Effect.-Life and Achievements:...
's assistants. Uhlenbeck, Goudsmit, and Kronig introduced the idea of the self-rotation of the electron, which would naturally give rise to an angular momentum vector in addition to the one associated with orbital motion (quantum numbers l and m).
The spin angular momentum is characterized by a quantum number; s = 1/2
Spin-½
In quantum mechanics, spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.- Overview :Particles...
specifically for electrons. In a way analogous to other quantized angular momenta, L, it is possible to obtain an expression for the total spin angular momentum:
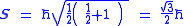
where
-
 is the reduced Planck constant.
is the reduced Planck constant.
The hydrogen spectra fine structure is observed as a doublet corresponding to two possibilities for the z-component of the angular momentum, where for any given direction z:
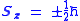
whose solution has only two possible z components for the electron. In the electron, the two different spin orientations are sometimes called "spin-up" or "spin-down".
The spin property of an electron would give rise to magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
, which was a requisite for the fourth quantum number. The electron spin magnetic moment is given by the formula:
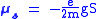
where
- e is the charge of the electron
- g is the Lande g-factorLandé g-factorIn physics, the Landé g-factor is a particular example of a g-factor, namely for an electron with both spin and orbital angular momenta. It is named after Alfred Landé, who first described it in 1921....
and by the equation:
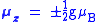
where
- g is the Lande g-factor
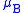 is the Bohr magneton.
is the Bohr magneton.
When atoms have even numbers of electrons the spin of each electron in each orbital has opposing orientation to that of its immediate neighbor(s). However, many atoms have an odd number of electrons or an arrangement of electrons in which there is an unequal number of "spin-up" and "spin-down" orientations. These atoms or electrons are said to have unpaired spins that are detected in electron spin resonance.
Detection of spin
When lines of the hydrogen spectrum are examined at very high resolution, they are found to be closely spaced doublets. This splitting is called fine structure, and was one of the first experimental evidences for electron spin. The direct observation of the electron's intrinsic angular momentum was achieved in the Stern–Gerlach experimentStern–Gerlach experiment
Important in the field of quantum mechanics, the Stern–Gerlach experiment, named after Otto Stern and Walther Gerlach, is a 1922 experiment on the deflection of particles, often used to illustrate basic principles of quantum mechanics...
.
The Stern–Gerlach experiment
The theory of spatial quantization of the spin moment of the momentum of electrons of atoms situated in the magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
needed to be proved experimentally. In 1920
1920 in science
The year 1920 in science and technology involved some significant events, listed below.-History of science and technology:* Newcomen Society founded in the United Kingdom for the study of the history of engineering and technology.-Medicine:...
(two years before the theoretical description of the spin was created) Otto Stern
Otto Stern
Otto Stern was a German physicist and Nobel laureate in physics.-Biography:Stern was born in Sohrau, now Żory in the German Empire's Kingdom of Prussia and studied at Breslau, now Wrocław in Lower Silesia....
and Walter Gerlach
Walter Gerlach
Walter Gerlach was a German physicist who co-discovered spin quantization in a magnetic field, the Stern-Gerlach effect.-Education:Gerlach was born in Biebrich, Hessen-Nassau....
observed it in the experiment they conducted.
- The atoms of silver from the source that was the furnace with boiling silver were leaded to the vacuum space. There (thanks to the thin slides) the flat beam of those atoms was created. Then the beam got into non-homogeneous magnetic field and incidenced a photographic plate. Using classic physical laws we would expect the single picture of the beam on the plate. Whereas the beam of the atoms passing through not homogenous magnetic field undergoes splitting. That is why Otto Stern and Walter Gerlach received the two lines on the photographic plate.
- The phenomena can be explained with the spatial quantization of the spin moment of momentum. In atoms the electrons are typically located in such way that in each pair of electrons there is one of the upward spin and one of the downward spin. So the whole spin of such pair is equal to zero. But, in the atom of silver on the outer shell, there is a single electron whose spin is not balanced by any electron.
- The circulating causes some magnetic dipole moment (it's like it was a very small magnet). There is a force moment in the magnetic field influencing the dipole that is turning it until its position is the same as the direction of the field B. There is some other force influencing the dipole in the field. When the dipole is directed the same as the magnetic field then the dipole is pulled by that force toward the strongest field. But, if the dipole is directed opposite to the field's, it is pushed away from the strongest field.
- So the atom of silver having one electron on the outer shell can be pulled in or out the space of a strongest magnetic field, what depends on the value of the magnetic spin quantum number. When the spin of the electron is equal +1/2 the atom is pulled out and when the spin is equal −1/2 the atom is pulled in. So during passing through the non-homogenous magnetic field the beam of the atoms of silver undergoes splitting into the two beams. Each of them consists of atoms whose outer electrons are of the same spin.
- In 19271927 in scienceThe year 1927 in science and technology involved some significant events, listed below.-Mathematics:* Publication of the 2nd edition of Principia Mathematica by Alfred North Whitehead and Bertrand Russell, one of the most important and seminal works in mathematical logic and philosophy.-Physics:*...
Phipps and Taylor conducted a similar experiment. This time they used atoms of hydrogen, not silver. They also observed that the beam of atoms undergoes splitting into two beams. - Later scientists conducted experiments using other atoms that have only one electron on the outer shell (copper, gold, sodium, potassium). Every time there were two lines achieved on the photographic plate.
- In the atom, not only electrons have spin: The elements of the nucleus also have spin. But protons and neutrons are much heavier than electrons (about 1836 times), and the magnetic dipole moment is inversely proportional to the mass. So the proton's and neutron's magnetic dipole momentum is much smaller than that of the whole atom. This small magnetic dipole was later measured by Stern, Frisch and Easterman.
Dirac equation solves spin
When the idea of electron spin was first introduced in 1925, even Wolfgang Pauli had trouble accepting Ralph KronigRalph Kronig
Ralph Kronig was a German-American physicist . He is noted for the discovery of particle spin and for his theory of x-ray absorption spectroscopy...
's model. The problem was not that a rotating charged particle would have given rise to a magnetic field but that the electron was so small that the equatorial speed of the electron would have to be greater than the speed of light for the magnetic moment to be of the observed strength.
In 1930, Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
developed a new version of the Schrödinger Wave Equation which was relativistically invariant
Lorentz covariance
In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
, and predicted the magnetic moment correctly, and at the same time treated the electron as a point particle. In the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
all four quantum numbers including the additional quantum number, s arose naturally during its solution.