
Spin-½
Encyclopedia
In quantum mechanics
, spin
is an intrinsic property of all elementary particle
s. Fermions, the particles that constitute ordinary matter, have half-integer
spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.
, neutron
, electron
, neutrino
, and quarks. The dynamics of spin-½ objects cannot be accurately described using classical physics
; they are among the simplest systems which require quantum mechanics
to describe them. As such, the study of the behavior of spin-½ systems forms a central part of quantum mechanics
.
A spin-½ particle is characterized by an angular momentum quantum number for spin (s) of 1/2. In solutions of the Schrödinger equation
, angular momentum is quantized according to this number, so that total spin angular momentum

However, the observed fine structure
when the electron is observed along one axis, such as the Z-axis, is quantized in terms of a magnetic quantum number
, which can be viewed as a quantization of a vector component of this total angular momentum, which can have only the values of ±½ħ.
Note that these values for angular momentum are functions only of the reduced Planck constant (the angular momentum of any photon
), with no dependence on mass or charge.
goes back experimentally to the results of the Stern–Gerlach experiment
. A beam of atoms is run through a strong inhomogeneous magnetic field, which then splits into N parts depending on the intrinsic angular momentum of the atoms. It was found that for silver atoms, the beam was split in two—the ground state therefore could not be integral, because even if the intrinsic angular momentum of the atoms were as small as possible, 1, the beam would be split into 3 parts, corresponding to atoms with Lz = −1, 0, and +1. The conclusion was that silver atoms had net intrinsic angular momentum of .
. Spin-½ particles can have a permanent magnetic moment
along the direction of their spin, and this magnetic moment gives rise to electromagnetic
interactions that depend on the spin. One such effect that was important in the discovery of spin is the Zeeman effect
.
Unlike in more complicated quantum mechanical systems, the spin of a spin-½ particle can be expressed as a linear combination
of just two eigenstates, or eigenspinor
s. These are traditionally labeled spin up and spin down. Because of this the quantum mechanical spin operators
can be represented as simple 2 × 2 matrices. These matrices are called the Pauli matrices
.
Creation and annihilation operators
can be constructed for spin-½ objects; these obey the same commutation
relations as other angular momentum operator
s.
is that the spin projection operators (which measure the spin along a given direction like x, y, or z), cannot be measured simultaneously. Physically, this means that it is ill defined what axis a particle is spinning about. A measurement of the z-component of spin destroys any information about the x and y components that might previously have been obtained.
It can be puzzling as to why a rotation of 720 degrees or two turns is necessary to return to the original state. This comes about because in quantum theory the state of a particle or system is represented by a complex probability amplitude
and then when a measurement is made on the system the probability of it coming out some way is given by the square of absolute value
of the appropriate amplitude.
Say you send a particle into a system with a detector that can be rotated where the probabilities of it detecting some state are affected by the rotation. When the system is rotated through 360 degrees the observed output and physics are the same as at the start but the amplitudes are changed for a spin-½ particle by a factor of −1 or a phase shift of half of 360 degrees. When the probabilities are calculated the −1 is squared and equals a factor of one so the predicted physics is same as in the starting position. Also in a spin-½ particle there are only two spin states and the amplitudes for both change by the same −1 factor so the interference effects are identical unlike the case for higher spins. The complex probability amplitudes are something of a theoretical construct and cannot be directly observed.
If the probability amplitudes changed by the same amount as the rotation of the equipment then they would have changed by a factor of −1 when the equipment was rotated by 180 degrees which when squared would predict the same output as at the start but this is wrong experimentally. If you rotate the detector 180 degrees the output with spin-½ particles can be different to what it would be if you did not hence the factor of a half is necessary to make the predictions of the theory match reality.
.
When spinors are used to describe the quantum states, quantum mechanical operators
are represented by 2 × 2, complex-valued Hermitian matrices.
For example, the spin projection operator Sz affects a measurement of the spin in the z direction.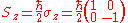
Sz operator has two eigenvalues, of ±, which correspond to the eigenvectors
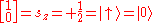
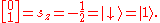
These vectors form a complete basis for the Hilbert space
describing the spin-½ particle. Thus, linear combinations of these two states can represent all possible states of the spin.
tried to modify the Schrödinger equation
so that it was consistent with Einstein's theory of relativity
, he found it was only possible by including matrices in the resulting Dirac Equation
, implying the wave must have multiple components leading to spin.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
is an intrinsic property of all elementary particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s. Fermions, the particles that constitute ordinary matter, have half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.
Overview
Particles having net spin ½ include the protonProton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
, neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
, electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, neutrino
Neutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
, and quarks. The dynamics of spin-½ objects cannot be accurately described using classical physics
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
; they are among the simplest systems which require quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
to describe them. As such, the study of the behavior of spin-½ systems forms a central part of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
A spin-½ particle is characterized by an angular momentum quantum number for spin (s) of 1/2. In solutions of the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, angular momentum is quantized according to this number, so that total spin angular momentum

However, the observed fine structure
Fine structure
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to first order relativistic corrections.The gross structure of line spectra is the line spectra predicted by non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy...
when the electron is observed along one axis, such as the Z-axis, is quantized in terms of a magnetic quantum number
Magnetic quantum number
In atomic physics, the magnetic quantum number is the third of a set of quantum numbers which describe the unique quantum state of an electron and is designated by the letter m...
, which can be viewed as a quantization of a vector component of this total angular momentum, which can have only the values of ±½ħ.
Note that these values for angular momentum are functions only of the reduced Planck constant (the angular momentum of any photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
), with no dependence on mass or charge.
Stern–Gerlach experiment
The necessity of introducing half-integral spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
goes back experimentally to the results of the Stern–Gerlach experiment
Stern–Gerlach experiment
Important in the field of quantum mechanics, the Stern–Gerlach experiment, named after Otto Stern and Walther Gerlach, is a 1922 experiment on the deflection of particles, often used to illustrate basic principles of quantum mechanics...
. A beam of atoms is run through a strong inhomogeneous magnetic field, which then splits into N parts depending on the intrinsic angular momentum of the atoms. It was found that for silver atoms, the beam was split in two—the ground state therefore could not be integral, because even if the intrinsic angular momentum of the atoms were as small as possible, 1, the beam would be split into 3 parts, corresponding to atoms with Lz = −1, 0, and +1. The conclusion was that silver atoms had net intrinsic angular momentum of .
General properties
Spin-½ objects are all fermions (a fact explained by the spin statistics theorem) and satisfy the Pauli exclusion principlePauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
. Spin-½ particles can have a permanent magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
along the direction of their spin, and this magnetic moment gives rise to electromagnetic
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
interactions that depend on the spin. One such effect that was important in the discovery of spin is the Zeeman effect
Zeeman effect
The Zeeman effect is the splitting of a spectral line into several components in the presence of a static magnetic field. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field...
.
Unlike in more complicated quantum mechanical systems, the spin of a spin-½ particle can be expressed as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of just two eigenstates, or eigenspinor
Eigenspinor
In quantum mechanics, eigenspinors are thought of as basis vectors representing the general spin state of a particle. Strictly speaking, they are not vectors at all, but in fact spinors...
s. These are traditionally labeled spin up and spin down. Because of this the quantum mechanical spin operators
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
can be represented as simple 2 × 2 matrices. These matrices are called the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
.
Creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
can be constructed for spin-½ objects; these obey the same commutation
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
relations as other angular momentum operator
Angular momentum operator
In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...
s.
Connection to the uncertainty principle
One consequence of the generalized uncertainty principleUncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
is that the spin projection operators (which measure the spin along a given direction like x, y, or z), cannot be measured simultaneously. Physically, this means that it is ill defined what axis a particle is spinning about. A measurement of the z-component of spin destroys any information about the x and y components that might previously have been obtained.
Complex Phase
Mathematically, quantum mechanical spin is not described by a vector as in classical angular momentum. It is described by a complex-valued vector with two components called a spinor. There are subtle differences between the behavior of spinors and vectors under coordinate rotations, stemming from the behavior of a vector space over a complex field.It can be puzzling as to why a rotation of 720 degrees or two turns is necessary to return to the original state. This comes about because in quantum theory the state of a particle or system is represented by a complex probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
and then when a measurement is made on the system the probability of it coming out some way is given by the square of absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the appropriate amplitude.
Say you send a particle into a system with a detector that can be rotated where the probabilities of it detecting some state are affected by the rotation. When the system is rotated through 360 degrees the observed output and physics are the same as at the start but the amplitudes are changed for a spin-½ particle by a factor of −1 or a phase shift of half of 360 degrees. When the probabilities are calculated the −1 is squared and equals a factor of one so the predicted physics is same as in the starting position. Also in a spin-½ particle there are only two spin states and the amplitudes for both change by the same −1 factor so the interference effects are identical unlike the case for higher spins. The complex probability amplitudes are something of a theoretical construct and cannot be directly observed.
If the probability amplitudes changed by the same amount as the rotation of the equipment then they would have changed by a factor of −1 when the equipment was rotated by 180 degrees which when squared would predict the same output as at the start but this is wrong experimentally. If you rotate the detector 180 degrees the output with spin-½ particles can be different to what it would be if you did not hence the factor of a half is necessary to make the predictions of the theory match reality.
Mathematical description
The quantum state of the spin of a spin-½ particle can be described by a complex-valued vector with two components called a two-component spinorSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
.
When spinors are used to describe the quantum states, quantum mechanical operators
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
are represented by 2 × 2, complex-valued Hermitian matrices.
For example, the spin projection operator Sz affects a measurement of the spin in the z direction.
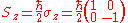
Sz operator has two eigenvalues, of ±, which correspond to the eigenvectors
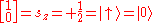
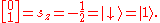
These vectors form a complete basis for the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
describing the spin-½ particle. Thus, linear combinations of these two states can represent all possible states of the spin.
Spin as a consequence of combining quantum theory and special relativity
When physicist Paul DiracPaul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
tried to modify the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
so that it was consistent with Einstein's theory of relativity
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
, he found it was only possible by including matrices in the resulting Dirac Equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
, implying the wave must have multiple components leading to spin.
See also
- SpinSpin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
- SpinorSpinorIn mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
- Fermions
- Pauli matricesPauli matricesThe Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
- Spin-statistics theoremSpin-statistics theoremIn quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
relating spin-1/2 and fermionic statistics

