Pauli exclusion principle
Encyclopedia
The Pauli exclusion principle is the quantum mechanical
principle that no two identical
fermions (particles with half-integer spin
) may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric
with respect to exchange of the particles. The principle was formulated by Austrian physicist Wolfgang Pauli
in 1925.
For example, no two electrons in a single atom can have the same four quantum number
s; if n, l, and ml are the same, ms must be different such that the electrons have opposite spins, and so on.
Integer spin particles, boson
s, are not subject to the Pauli exclusion principle: any number of identical bosons can occupy the same quantum state, as with, for instance, photons produced by a laser
and Bose-Einstein condensate.
is made—proton
s, electron
s, and neutron
s—are all subject to it, and the structure and chemical behavior of atoms is due to it. It causes atoms to take up the space they do, since electrons cannot all congregate in the lowest-energy state but must occupy higher energy states at a distance from lower-energy electrons, therefore matter made of atoms occupies space rather than being condensed. As such, the Pauli exclusion principle underpins many properties of everyday matter, from its large-scale stability to the periodic table of the elements
.
Fermions, particle
s with antisymmetric wave functions, obey the Pauli exclusion principle. In addition to the electron, proton and neutron, these include neutrino
s and quark
s (the constituent particles of protons and neutrons), and some atom
s such as helium-3
. All fermions have "half-integer spin
", i.e. their intrinsic angular momentum
value is
(reduced Planck's constant) times a half-integer
(1/2, 3/2, 5/2, etc.). In the theory of quantum mechanics
fermions are described by antisymmetric states
. Particles with integer spin (called bosons) have symmetric wave functions; unlike fermions they may share the same quantum states. Bosons include the photon
, the Cooper pairs which are responsible for superconductivity
, and the W and Z bosons
. (Fermions take their name from the Fermi–Dirac statistical distribution that they obey, and bosons from their Bose–Einstein distribution
).
, for example, the third of his six postulates of chemical behavior states that the atom tends to hold an even number of electrons in the shell and especially to hold eight electrons which are normally arranged symmetrically at the eight corners of a cube (see: cubical atom
). In 1919 chemist Irving Langmuir
suggested that the periodic table
could be explained if the electrons in an atom were connected or clustered in some manner. Groups of electrons were thought to occupy a set of electron shell
s about the nucleus. In 1922, Niels Bohr
updated his model of the atom by assuming that certain numbers of electrons (for example 2, 8 and 18) corresponded to stable "closed shells".
Pauli looked for an explanation for these numbers, which were at first only empirical
.
At the same time he was trying to explain experimental results in the Zeeman effect
in atomic spectroscopy
and in ferromagnetism
. He found an essential clue in a 1924 paper by E.C.Stoner
which pointed out that for a given value of the principal quantum number
(n), the number of energy levels of a single electron in the alkali metal
spectra in an external magnetic field, where all degenerate energy level
s are separated, is equal to the number of electrons in the closed shell of the rare gases for the same value of n. This led Pauli to realize that the complicated numbers of electrons in closed shells can be reduced to the simple rule of one per state, if the electron states are defined using four quantum numbers. For this purpose he introduced a new two-valued quantum number, identified by Samuel Goudsmit and George Uhlenbeck as electron spin.
in which one particle is in state
and the other in state 
:
and antisymmetry under exchange means that A(x,y) = -A(y,x). This implies that A(x,x)=0, which is Pauli exclusion. It is true in any basis, since unitary changes of basis keep antisymmetric matrices antisymmetric, although strictly speaking, the quantity A(x,y) is not a matrix but an antisymmetric rank-two tensor
.
Conversely, if the diagonal quantities A(x,x) are zero in every basis, then the wavefunction component: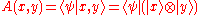
is necessarily antisymmetric. To prove it, consider the matrix element:
This is zero, because the two particles have zero probability to both be in the superposition state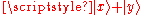
. But this is equal to
The first and last terms on the right hand side are diagonal elements and are zero, and the whole sum is equal to zero. So the wavefunction matrix elements obey:
.
or
, particles with integer spin occupy symmetric quantum states, and particles with half-integer spin occupy antisymmetric states; furthermore, only integer or half-integer values of spin are allowed by the principles of quantum mechanics.
In relativistic quantum field theory
, the Pauli principle follows from applying a rotation operator in imaginary time to particles of half-integer spin. Since, nonrelativistically, particles can have any statistics and any spin, there is no way to prove a spin-statistics theorem in nonrelativistic quantum mechanics.
In one dimension, bosons, as well as fermions, can obey the exclusion principle. A one-dimensional Bose gas with delta function repulsive interactions of infinite strength is equivalent to a gas of free fermions. The reason for this is that, in one dimension, exchange of particles requires that they pass through each other; for infinitely strong repulsion this cannot happen. This model is described by a quantum nonlinear Schrödinger equation
. In momentum space the exclusion principle is valid also for finite repulsion in a Bose gas with delta function interactions, as well as for interacting spins
and Hubbard model
in one dimension, and for other models solvable by Bethe ansatz
. The ground state
in models solvable by Bethe ansatz is a Fermi sphere
.
structure of atom
s and the way atoms share electrons, explaining the variety of chemical elements and their chemical combinations. An electrically neutral
atom contains bound electron
s equal in number to the protons in the nucleus
. Electrons, being fermions, cannot occupy the same quantum state, so electrons have to "stack" within an atom, i.e. have different momenta while at the same place.
An example is the neutral helium
atom, which has two bound electrons, both of which can occupy the lowest-energy (1s
) states by acquiring opposite spin; as spin is part of the quantum state of the electron, the two electrons are in different quantum states and do not violate the Pauli principle. However, the spin can take only two different values (eigenvalues). In a lithium
atom, with three bound electrons, the third electron cannot reside in a 1s state, and must occupy one of the higher-energy 2s states instead. Similarly, successively larger elements must have shells of successively higher energy. The chemical properties of an element largely depend on the number of electrons in the outermost shell; atoms with different numbers of shells but the same number of electrons in the outermost shell have similar properties, which gives rise to the periodic table of the elements
.
s and semi-conductors, free electrons have to share entire bulk space. Thus, their energy levels stack up, creating band structure out of each atomic energy level
. In strong conductors (metal
s) electrons are so degenerate
that they can not even contribute much to the thermal capacity of a metal. Many mechanical, electrical, magnetic, optical and chemical properties of solids are the direct consequence of Pauli exclusion.
of Heisenberg. However, stability of large systems with many electrons and many nuclei is a different matter, and requires the Pauli exclusion principle.
It has been shown that the Pauli exclusion principle is responsible for the fact that ordinary bulk matter is stable and occupies volume. This suggestion was first made in 1931 by Paul Ehrenfest
, who pointed out that the electrons of each atom cannot all fall into the lowest-energy orbital and must occupy successively larger shells. Atoms therefore occupy a volume and cannot be squeezed too closely together.
A more rigorous proof was provided in 1967 by Freeman Dyson
and Andrew Lenard, who considered the balance of attractive (electron-nuclear) and repulsive (electron-electron and nuclear-nuclear) forces and showed that ordinary matter would collapse and occupy a much smaller volume without the Pauli principle. The consequence of the Pauli principle here is that electrons of the same spin are kept apart by a repulsive exchange interaction
, which is a short-range effect, acting simultaneously with the long-range electrostatic or coulombic force. This effect is partly responsible for the everyday observation in the macroscopic world that two solid objects cannot be in the same place in the same time.
that, in sufficiently intense gravitational fields, matter collapses to form a black hole
.
Astronomy provides a spectacular demonstration of the effect of the Pauli principle, in the form of white dwarf
and neutron star
s. In both types of body, atomic structure is disrupted by large gravitation
al forces, leaving the constituents supported by "degeneracy pressure" alone. This exotic form of matter is known as degenerate matter
. In white dwarfs atoms are held apart by electron degeneracy pressure
. In neutron stars, subject to even stronger gravitational forces, electrons have merged with proton
s to form neutron
s. Neutrons are capable of producing an even higher degeneracy pressure, albeit over a shorter range. This can stabilize neutron stars from further collapse, but at a smaller size and higher density
than a white dwarf. Neutrons are the most "rigid" objects known; their Young modulus (or more accurately, bulk modulus
) is 20 orders of magnitude larger than that of diamond
. However, even this enormous rigidity can be overcome by the gravitational field
of a massive star or by the pressure of a supernova
, leading to the formation of a black hole
.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
principle that no two identical
Identical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
fermions (particles with half-integer spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
) may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
with respect to exchange of the particles. The principle was formulated by Austrian physicist Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
in 1925.
For example, no two electrons in a single atom can have the same four quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s; if n, l, and ml are the same, ms must be different such that the electrons have opposite spins, and so on.
Integer spin particles, boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s, are not subject to the Pauli exclusion principle: any number of identical bosons can occupy the same quantum state, as with, for instance, photons produced by a laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
and Bose-Einstein condensate.
Overview
The three types of particles from which the ordinary atomAtom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
is made—proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s, electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s, and neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s—are all subject to it, and the structure and chemical behavior of atoms is due to it. It causes atoms to take up the space they do, since electrons cannot all congregate in the lowest-energy state but must occupy higher energy states at a distance from lower-energy electrons, therefore matter made of atoms occupies space rather than being condensed. As such, the Pauli exclusion principle underpins many properties of everyday matter, from its large-scale stability to the periodic table of the elements
Periodic table
The periodic table of the chemical elements is a tabular display of the 118 known chemical elements organized by selected properties of their atomic structures. Elements are presented by increasing atomic number, the number of protons in an atom's atomic nucleus...
.
Fermions, particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s with antisymmetric wave functions, obey the Pauli exclusion principle. In addition to the electron, proton and neutron, these include neutrino
Neutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
s and quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s (the constituent particles of protons and neutrons), and some atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s such as helium-3
Helium-3
Helium-3 is a light, non-radioactive isotope of helium with two protons and one neutron. It is rare on Earth, and is sought for use in nuclear fusion research...
. All fermions have "half-integer spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
", i.e. their intrinsic angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
value is
(reduced Planck's constant) times a half-integerHalf-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
(1/2, 3/2, 5/2, etc.). In the theory of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
fermions are described by antisymmetric states
Identical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
. Particles with integer spin (called bosons) have symmetric wave functions; unlike fermions they may share the same quantum states. Bosons include the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
, the Cooper pairs which are responsible for superconductivity
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
, and the W and Z bosons
W and Z bosons
The W and Z bosons are the elementary particles that mediate the weak interaction; their symbols are , and . The W bosons have a positive and negative electric charge of 1 elementary charge respectively and are each other's antiparticle. The Z boson is electrically neutral and its own...
. (Fermions take their name from the Fermi–Dirac statistical distribution that they obey, and bosons from their Bose–Einstein distribution
Bose–Einstein statistics
In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...
).
History
In the early 20th century it became evident that atoms and molecules with even numbers of electrons are more chemically stable than those with odd numbers of electrons. In the famous 1916 article The Atom and the Molecule by Gilbert N. LewisGilbert N. Lewis
Gilbert Newton Lewis was an American physical chemist known for the discovery of the covalent bond , his purification of heavy water, his reformulation of chemical thermodynamics in a mathematically rigorous manner accessible to ordinary chemists, his theory of Lewis acids and...
, for example, the third of his six postulates of chemical behavior states that the atom tends to hold an even number of electrons in the shell and especially to hold eight electrons which are normally arranged symmetrically at the eight corners of a cube (see: cubical atom
Cubical atom
The cubical atom was an early atomic model in which electrons were positioned at the eight corners of a cube in a non-polar atom or molecule. This theory was developed in 1902 by Gilbert N. Lewis and published in 1916 in the famous article "The Atom and the Molecule" and used to account for the...
). In 1919 chemist Irving Langmuir
Irving Langmuir
Irving Langmuir was an American chemist and physicist. His most noted publication was the famous 1919 article "The Arrangement of Electrons in Atoms and Molecules" in which, building on Gilbert N. Lewis's cubical atom theory and Walther Kossel's chemical bonding theory, he outlined his...
suggested that the periodic table
Periodic table
The periodic table of the chemical elements is a tabular display of the 118 known chemical elements organized by selected properties of their atomic structures. Elements are presented by increasing atomic number, the number of protons in an atom's atomic nucleus...
could be explained if the electrons in an atom were connected or clustered in some manner. Groups of electrons were thought to occupy a set of electron shell
Electron shell
An electron shell may be thought of as an orbit followed by electrons around an atom's nucleus. The closest shell to the nucleus is called the "1 shell" , followed by the "2 shell" , then the "3 shell" , and so on further and further from the nucleus. The shell letters K,L,M,.....
s about the nucleus. In 1922, Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
updated his model of the atom by assuming that certain numbers of electrons (for example 2, 8 and 18) corresponded to stable "closed shells".
Pauli looked for an explanation for these numbers, which were at first only empirical
Empirical relationship
In science, an empirical relationship is one based solely on observation rather than theory. An empirical relationship requires only confirmatory data irrespective of theoretical basis. Sometimes theoretical explanations for what were initially empirical relationships are found, in which case the...
.
At the same time he was trying to explain experimental results in the Zeeman effect
Zeeman effect
The Zeeman effect is the splitting of a spectral line into several components in the presence of a static magnetic field. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field...
in atomic spectroscopy
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
and in ferromagnetism
Ferromagnetism
Ferromagnetism is the basic mechanism by which certain materials form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished...
. He found an essential clue in a 1924 paper by E.C.Stoner
Edmund Clifton Stoner
Edmund Clifton Stoner was a British theoretical physicist. He is principally known for his work on the origin and nature of itinerant ferromagnetism , including the collective electron theory of ferromagnetism...
which pointed out that for a given value of the principal quantum number
Principal quantum number
In atomic physics, the principal quantum symbolized as n is the firstof a set of quantum numbers of an atomic orbital. The principal quantum number can only have positive integer values...
(n), the number of energy levels of a single electron in the alkali metal
Alkali metal
The alkali metals are a series of chemical elements in the periodic table. In the modern IUPAC nomenclature, the alkali metals comprise the group 1 elements, along with hydrogen. The alkali metals are lithium , sodium , potassium , rubidium , caesium , and francium...
spectra in an external magnetic field, where all degenerate energy level
Degenerate energy level
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
s are separated, is equal to the number of electrons in the closed shell of the rare gases for the same value of n. This led Pauli to realize that the complicated numbers of electrons in closed shells can be reduced to the simple rule of one per state, if the electron states are defined using four quantum numbers. For this purpose he introduced a new two-valued quantum number, identified by Samuel Goudsmit and George Uhlenbeck as electron spin.
Connection to quantum state symmetry
The Pauli exclusion principle with a single-valued many-particle wavefunction is equivalent to requiring the wavefunction to be antisymmetric. An antisymmetric two-particle state is represented as a sum of statesSuperposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
in which one particle is in state
and the other in state :and antisymmetry under exchange means that A(x,y) = -A(y,x). This implies that A(x,x)=0, which is Pauli exclusion. It is true in any basis, since unitary changes of basis keep antisymmetric matrices antisymmetric, although strictly speaking, the quantity A(x,y) is not a matrix but an antisymmetric rank-two tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
.
Conversely, if the diagonal quantities A(x,x) are zero in every basis, then the wavefunction component:
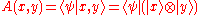
is necessarily antisymmetric. To prove it, consider the matrix element:
This is zero, because the two particles have zero probability to both be in the superposition state
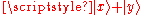. But this is equal toThe first and last terms on the right hand side are diagonal elements and are zero, and the whole sum is equal to zero. So the wavefunction matrix elements obey:
.or
The Pauli principle in advanced quantum theory
According to the spin-statistics theoremSpin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
, particles with integer spin occupy symmetric quantum states, and particles with half-integer spin occupy antisymmetric states; furthermore, only integer or half-integer values of spin are allowed by the principles of quantum mechanics.
In relativistic quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the Pauli principle follows from applying a rotation operator in imaginary time to particles of half-integer spin. Since, nonrelativistically, particles can have any statistics and any spin, there is no way to prove a spin-statistics theorem in nonrelativistic quantum mechanics.
In one dimension, bosons, as well as fermions, can obey the exclusion principle. A one-dimensional Bose gas with delta function repulsive interactions of infinite strength is equivalent to a gas of free fermions. The reason for this is that, in one dimension, exchange of particles requires that they pass through each other; for infinitely strong repulsion this cannot happen. This model is described by a quantum nonlinear Schrödinger equation
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
. In momentum space the exclusion principle is valid also for finite repulsion in a Bose gas with delta function interactions, as well as for interacting spins
Heisenberg model (quantum)
The Heisenberg model is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spin of the magnetic systems are treated quantum mechanically...
and Hubbard model
Hubbard model
The Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
in one dimension, and for other models solvable by Bethe ansatz
Bethe ansatz
In physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
. The ground state
Stationary state
In quantum mechanics, a stationary state is an eigenvector of the Hamiltonian, implying the probability density associated with the wavefunction is independent of time . This corresponds to a quantum state with a single definite energy...
in models solvable by Bethe ansatz is a Fermi sphere
Fermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
.
Atoms and the Pauli principle
The Pauli exclusion principle helps explain a wide variety of physical phenomena. One particularly important consequence of the principle is the elaborate electron shellElectron configuration
In atomic physics and quantum chemistry, electron configuration is the arrangement of electrons of an atom, a molecule, or other physical structure...
structure of atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s and the way atoms share electrons, explaining the variety of chemical elements and their chemical combinations. An electrically neutral
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
atom contains bound electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s equal in number to the protons in the nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
. Electrons, being fermions, cannot occupy the same quantum state, so electrons have to "stack" within an atom, i.e. have different momenta while at the same place.
An example is the neutral helium
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...
atom, which has two bound electrons, both of which can occupy the lowest-energy (1s
Electron shell
An electron shell may be thought of as an orbit followed by electrons around an atom's nucleus. The closest shell to the nucleus is called the "1 shell" , followed by the "2 shell" , then the "3 shell" , and so on further and further from the nucleus. The shell letters K,L,M,.....
) states by acquiring opposite spin; as spin is part of the quantum state of the electron, the two electrons are in different quantum states and do not violate the Pauli principle. However, the spin can take only two different values (eigenvalues). In a lithium
Lithium
Lithium is a soft, silver-white metal that belongs to the alkali metal group of chemical elements. It is represented by the symbol Li, and it has the atomic number 3. Under standard conditions it is the lightest metal and the least dense solid element. Like all alkali metals, lithium is highly...
atom, with three bound electrons, the third electron cannot reside in a 1s state, and must occupy one of the higher-energy 2s states instead. Similarly, successively larger elements must have shells of successively higher energy. The chemical properties of an element largely depend on the number of electrons in the outermost shell; atoms with different numbers of shells but the same number of electrons in the outermost shell have similar properties, which gives rise to the periodic table of the elements
Periodic table
The periodic table of the chemical elements is a tabular display of the 118 known chemical elements organized by selected properties of their atomic structures. Elements are presented by increasing atomic number, the number of protons in an atom's atomic nucleus...
.
Solid state properties and the Pauli principle
In conductorElectrical conductor
In physics and electrical engineering, a conductor is a material which contains movable electric charges. In metallic conductors such as copper or aluminum, the movable charged particles are electrons...
s and semi-conductors, free electrons have to share entire bulk space. Thus, their energy levels stack up, creating band structure out of each atomic energy level
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
. In strong conductors (metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s) electrons are so degenerate
Degenerate energy level
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
that they can not even contribute much to the thermal capacity of a metal. Many mechanical, electrical, magnetic, optical and chemical properties of solids are the direct consequence of Pauli exclusion.
Stability of matter
The stability of the electrons in an atom itself is not related to the exclusion principle, but is described by the quantum theory of the atom. The underlying idea is that close approach of an electron to the nucleus of the atom necessarily increases its kinetic energy, an application of the uncertainty principleUncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
of Heisenberg. However, stability of large systems with many electrons and many nuclei is a different matter, and requires the Pauli exclusion principle.
It has been shown that the Pauli exclusion principle is responsible for the fact that ordinary bulk matter is stable and occupies volume. This suggestion was first made in 1931 by Paul Ehrenfest
Paul Ehrenfest
Paul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...
, who pointed out that the electrons of each atom cannot all fall into the lowest-energy orbital and must occupy successively larger shells. Atoms therefore occupy a volume and cannot be squeezed too closely together.
A more rigorous proof was provided in 1967 by Freeman Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
and Andrew Lenard, who considered the balance of attractive (electron-nuclear) and repulsive (electron-electron and nuclear-nuclear) forces and showed that ordinary matter would collapse and occupy a much smaller volume without the Pauli principle. The consequence of the Pauli principle here is that electrons of the same spin are kept apart by a repulsive exchange interaction
Exchange interaction
In physics, the exchange interaction is a quantum mechanical effect without classical analog which increases or decreases the expectation value of the energy or distance between two or more identical particles when their wave functions overlap...
, which is a short-range effect, acting simultaneously with the long-range electrostatic or coulombic force. This effect is partly responsible for the everyday observation in the macroscopic world that two solid objects cannot be in the same place in the same time.
Astrophysics and the Pauli principle
Dyson and Lenard did not consider the extreme magnetic or gravitational forces which occur in some astronomical objects. In 1995 Elliott Lieb and coworkers showed that the Pauli principle still leads to stability in intense magnetic fields such as in neutron stars, although at a much higher density than in ordinary matter. It is a consequence of general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
that, in sufficiently intense gravitational fields, matter collapses to form a black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
.
Astronomy provides a spectacular demonstration of the effect of the Pauli principle, in the form of white dwarf
White dwarf
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
and neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
s. In both types of body, atomic structure is disrupted by large gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
al forces, leaving the constituents supported by "degeneracy pressure" alone. This exotic form of matter is known as degenerate matter
Degenerate matter
Degenerate matter is matter that has such extraordinarily high density that the dominant contribution to its pressure is attributable to the Pauli exclusion principle. The pressure maintained by a body of degenerate matter is called the degeneracy pressure, and arises because the Pauli principle...
. In white dwarfs atoms are held apart by electron degeneracy pressure
Electron degeneracy pressure
Electron degeneracy pressure is a particular manifestation of the more general phenomenon of quantum degeneracy pressure. The Pauli Exclusion Principle disallows two half integer spin particles from occupying the same quantum state at a given time. The resulting emergent repulsive force is...
. In neutron stars, subject to even stronger gravitational forces, electrons have merged with proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s to form neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s. Neutrons are capable of producing an even higher degeneracy pressure, albeit over a shorter range. This can stabilize neutron stars from further collapse, but at a smaller size and higher density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
than a white dwarf. Neutrons are the most "rigid" objects known; their Young modulus (or more accurately, bulk modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
) is 20 orders of magnitude larger than that of diamond
Diamond
In mineralogy, diamond is an allotrope of carbon, where the carbon atoms are arranged in a variation of the face-centered cubic crystal structure called a diamond lattice. Diamond is less stable than graphite, but the conversion rate from diamond to graphite is negligible at ambient conditions...
. However, even this enormous rigidity can be overcome by the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
of a massive star or by the pressure of a supernova
Supernova
A supernova is a stellar explosion that is more energetic than a nova. It is pronounced with the plural supernovae or supernovas. Supernovae are extremely luminous and cause a burst of radiation that often briefly outshines an entire galaxy, before fading from view over several weeks or months...
, leading to the formation of a black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
.
See also
- Exchange forceExchange forceIn physics the term exchange force has been used to describe two distinct concepts which should not be confused.-Exchange of force carriers in particle physics:...
- Exchange interactionExchange interactionIn physics, the exchange interaction is a quantum mechanical effect without classical analog which increases or decreases the expectation value of the energy or distance between two or more identical particles when their wave functions overlap...
- Exchange symmetryExchange symmetryExchange symmetry is derived from a fundamental postulate of quantum statistics, which states that no observable physical quantity should change after exchanging two identical particles...
- Hund's rule
- Fermi holeFermi holeThe idea of a Fermi hole requires some background in the idea of anti-symmetrized wavefunctions. The Pauli exclusion principle is the "rule" that no more than two electrons can be in the same orbital. The "rule" traces to a deep algebraic property of nature that has nothing whatsoever to do with...
External links
- Nobel Lecture: Exclusion Principle and Quantum Mechanics Pauli's own account of the development of the Exclusion Principle.
- The Exclusion Principle (1997), Pauli's exclusion rules vs. the Aspden exclusion rules (plus the radiation factor, Larmor radiation formula, elliptical motion, the quantum states, occupancy of electron shells, nature of ferromagnetism, ...).