Quantum state
Encyclopedia
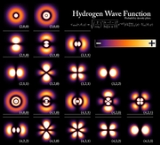
A quantum state is a set of mathematical variables that fully describes a quantum system. For example, the set of 4 numbers {
, 
, 
, 
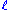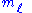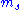} defines the state of an electron within a hydrogen atom and are known as the electron's quantum number
s. Other examples could be "given direction and energy, or some other given condition", when we are talking about scattering. More generally, the state of the system is represented by a single vector known as a ket
.
Typically, one postulates some experimental apparatus and procedure which "prepares" this quantum state; the mathematical object reflects the setup of the apparatus. Quantum states can be either pure or mixed. Pure states cannot be described as a mixture of others. Mixed states correspond to an experiment involving a random process that blends pure states together.
When performing a particular measurement
on a quantum state, the result is usually described by a probability distribution
, and the form that this distribution takes is completely determined by the quantum state and the observable
describing the measurement. These probability distributions are necessary for both mixed states and pure states: It is impossible in quantum mechanics (unlike classical mechanics) to have any state whose properties are all fixed and certain. This is exemplified by the Heisenberg uncertainty principle, and reflects a core difference between classical
and quantum physics.
Mathematically, a pure quantum state is typically represented by a vector in a Hilbert space
which is a generalization of our more usual three dimensional space. In a Hilbert space the co-ordinates are complex numbers, a complex kind of distance between points is defined and infinite series of numbers are made to converge. In physics, bra-ket notation
is often used to denote such vectors. Linear combination
s (superpositions
) of vectors can describe interference phenomena. Mixed quantum states are described by density matrices
.
In a more general mathematical context, quantum states can be understood as positive normalized linear functional
s on a C* algebra; see GNS construction.
is a complete description of the parameters of the experiment.
To understand this rather abstract notion, it is useful to first explore it in an example from classical mechanics.
Consider an experiment with a (non-quantum) particle of mass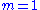
that moves freely, and without friction, in one spatial direction.
We put the particle at initial position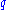
and start the experiment at time 
by pushing the particle with some speed and in some direction. Doing this, we determine the initial momentum
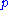
of the particle. These initial conditions are what characterizes the state
of the system,
formally denoted as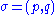
. We say that we prepare the state of the system
by fixing its initial conditions.
At a later time
, we conduct measurements on the particle.
The measurements we can perform on this simple
system are essentially its position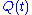
at time 
, its momentum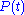 
,
and combinations of these.
Here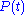
and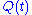 
refer to the measurable quantities (observables)
of the system as such, not the specific results they produce in a certain run of the experiment.
However, knowing the state
of the system, we can compute the
value of the observables in the specific state, i.e. the results that our measurements will produce,
depending on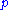
and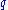 
.
We denote these values as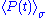
and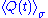 
.
In our simple example, it is well known that the particle moves with constant velocity; therefore,
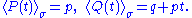
Now suppose that we start the particle with a random initial position and momentum.
(For argument's sake, we may suppose that the particle is pushed away at
by some apparatus which is controlled by a random number generator.)
The state
of the system is now not described by two numbers
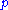and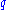 
, but rather by two probability distributions.
The observables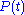
and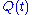 
will produce random results now;
they become random variable
s, and their values in a single measurement cannot be predicted.
However, if we repeat the experiment sufficiently often,
always preparing the same state
, we can predict the expectation value
of the observables (their statistical mean
) in the state
. The expectation
value of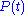
is again denoted by 
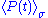, etc.
These "statistical" states of the system are called mixed states,
as opposed to the pure states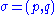
discussed further below.
Abstractly, mixed states arise as a statistical mixture
of pure states.
In quantum systems, the conceptual distinction between observables and states persists just as described above.
The state
of the system is fixed by the way the physicist prepares the experiment
(e.g., how the physicist adjusts the particle source). As above, there is a distinction between pure states and
mixed states, the latter being statistical mixtures of the former.
However, some important differences arise in comparison with classical mechanics.
In quantum theory, even pure states show statistical behaviour.
Regardless of how carefully we prepare the state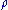
of the system,
measurement results are not repeatable in general, and we must understand the expectation value
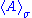of an observable 
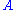as a statistical mean.
It is this mean that is predicted by physical theories.
For any fixed observable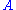
, it is generally
possible to prepare a pure state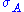
such that 
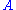has a fixed
value in this state: If we repeat the experiment several times, each time
measuring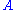
, we will always obtain the same measurement result,
without any random behaviour.
Such pure states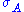
are called eigenstates of 
.
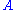However, it is impossible to prepare a simultaneous eigenstate
for all observables. For example, we cannot prepare a state
such that both the position measurement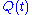
and the momentum measurement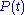
(at the same time
) produce "sharp" results;
at least one of them will exhibit random behaviour.
This is the content of the Heisenberg uncertainty relation
.
Moreover, in contrast to classical mechanics, it is unavoidable that
performing a measurement on the system generally changes its state.
More precisely: After measuring an observable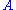
,
the system will be in an eigenstate of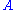
; thus the state has changed, unless the system was already in that eigenstate.
This expresses a kind of logical consistency: If we measure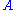
twice in the same
run of the experiment, the measurements being directly consecutive in time, then they will
produce the same results. This has some strange consequences however:
Consider two observables,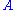
and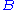 
, where 
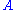corresponds
to a measurement earlier in time than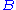
.
Suppose that the system is in an eigenstate of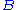
.
If we measure only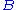
, we will not notice statistical behaviour.
If we measure first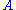
and then 
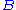in the same run of the experiment,
the system will transfer to an eigenstate of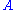
after the first measurement,
and we will generally notice that the results of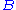
are statistical.
Thus, quantum mechanical measurements influence one another, and it is important
in which order they are performed.
Another feature of quantum states becomes relevant if we consider a physical system that
consists of multiple subsystems; for example, an experiment with two particles rather than one.
Quantum physics allows for certain states, called entangled states,
that show certain statistical correlations between measurements on the two particles
which cannot be explained by classical theory. For details, see entanglement
.
These entangled states lead to experimentally testable properties (Bell's theorem
)
that allow us to distinguish between quantum theory and alternative classical (non-quantum) models.
, 
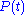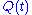
to be dependent on time, while the state
was fixed once at the beginning of the experiment.
This approach is called the Heisenberg picture
. One can, equivalently, treat the observables as fixed,
while the state of the system depends on time; that is known as the Schrödinger picture
.
Conceptually (and mathematically), both approaches are equivalent; choosing one of them is a matter of convention.
Both viewpoints are used in quantum theory. While non-relativistic quantum mechanics
is usually formulated
in terms of the Schrödinger picture, the Heisenberg picture is often preferred in a relativistic context,
that is, for quantum field theory
.
Compare with Dirac picture.
, as follows. Any given system is identified with some Hilbert space
, such that each vector in the Hilbert space (apart from the origin) corresponds to a pure quantum state. In addition, two vectors that differ only by a nonzero complex scalar
correspond to the same state (in other words, each pure state is a ray in the Hilbert space; equivalently, a point in the projective Hilbert space
.).
Alternatively, many authors choose to only consider normalized vectors (vectors of norm
1) as corresponding to quantum states. In this case, the set of all pure states corresponds to the unit sphere
of a Hilbert space, with the proviso that two normalized vectors correspond to the same state if they differ only by a complex scalar of absolute value 1, which is called the phase factor.
s, and Hermitian conjugation. In order to make such calculations more straightforward, and to obviate the need (in some contexts) to fully understand the underlying linear algebra, Paul Dirac
invented a notation to describe quantum states, known as bra-ket notation. Although the details of this are beyond the scope of this article (see the article Bra-ket notation
), some consequences of this are:
, a discrete variable m exists, corresponding to the value of the z-component of the spin
vector. This can be thought of as a kind of intrinsic angular momentum. However, it does not appear at all in classical mechanics and arises from Dirac's relativistic generalization of the theory. As a consequence, the quantum state of a system of N particles is described by a function with four variables per particle, e.g.
. Here, the variables mν assume values from the set {
}, where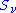 
(in units of Planck's reduced constant 
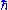), is either a non-negative integer (0,1,2...; boson
s), or semi-integer (1/2,3/2,5/2,...; fermion
s). Moreover, in the case of identical particles, the above N-particle function must either be symmetrized (in the bosonic case) or anti-symmetrized (in the fermionic case) with respect to the particle numbers.
Electrons are fermions with S = 1/2, photons (quanta of light) are bosons with S = 1.
Apart from the symmetrization or anti-symmetrization, N-particle states can thus simply be obtained by tensor product
s of one-particle states, to which we return herewith.
, if a basis
is chosen for the Hilbert space of a system, then any ket can be expanded as a linear combination
of those basis elements. Symbolically, given basis kets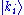
, any ket 
can be written
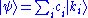
where ci are complex numbers. In physical terms, this is described by saying that
has been expressed as a quantum superposition of the states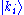 
. If the basis kets are chosen to be orthonormal
(as is often the case), then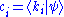
.
One property worth noting is that the normalized states
are characterized by
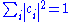
Expansions of this sort play an important role in measurement in quantum mechanics. In particular, if the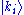
are eigenstates (with eigenvalues 
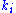) of an observable, and that observable is measured on the normalized state 
, then the probability that the result of the measurement is ki is |ci|2. (The normalization condition above mandates that the total sum of probabilities is equal to one.)
A particularly important example is the position basis, which is the basis consisting of eigenstates of the observable which corresponds to measuring position. If these eigenstates are nondegenerate (for example, if the system is a single, spinless
particle), then any ket
is associated with a complex-valued function of three-dimensional space:
.
This function is called the wavefunction
corresponding to
.
of them can be formed. If
and 
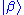are two kets corresponding to quantum states, the ket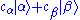
is a different quantum state (possibly not normalized). Note that which quantum state it is depends on both the amplitudes and phases (arguments) of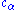
and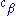 
. In other words, for example, even though 
and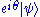 
(for real θ) correspond to the same physical quantum state, they are not interchangeable, since for example 
and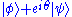 
do not (in general) correspond to the same physical state. However, 
and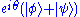 
do correspond to the same physical state. This is sometimes described by saying that "global" phase factors are unphysical, but "relative" phase factors are physical and important.
One example of a quantum interference phenomenon that arises from superposition is the double-slit experiment
. The photon
state is a superposition of two different states, one of which corresponds to the photon having passed through the left slit, and the other corresponding to passage through the right slit. The relative phase of those two states has a value which depends on the distance from each of the two slits. Depending on what that phase is, the interference is constructive at some locations and destructive in others, creating the interference pattern.
Another example of the importance of relative phase in quantum superposition is Rabi oscillations, where the relative phase of two states varies in time due to the Schrödinger equation
. The resulting superposition ends up oscillating back and forth between two different states.
). Equivalently, a mixed-quantum state on a given quantum system described by a Hilbert space H naturally arises as a pure quantum state (called a purification) on a larger bipartite system H tensor K, the other half of which is inaccessible to the observer.
A mixed state cannot be described as a ket vector. Instead, it is described by its associated density matrix (or density operator), usually denoted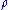
. Note that density matrices can describe both mixed and pure states, treating them on the same footing.
The density matrix is defined as
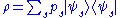
where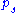
is the fraction of the ensemble in each pure state 
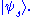Here, one typically uses a one-particle formalism to describe the average behaviour of an N-particle system.
A simple criterion for checking whether a density matrix is describing a pure or mixed state is that the trace
of ρ2 is equal to 1 if the state is pure, and less than 1 if the state is mixed. Another, equivalent, criterion is that the von Neumann entropy
is 0 for a pure state, and strictly positive for a mixed state.
The rules for measurement in quantum mechanics are particularly simple to state in terms of density matrices. For example, the ensemble average (expectation value
) of a measurement corresponding to an observable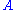
is given by
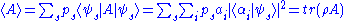
where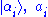
are eigenkets and eigenvalues, respectively, for the operator 
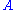, and tr denotes trace. It is important to note that two types of averaging are occurring, one being a quantum average over the basis kets 
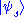of the pure states, and the other being a statistical average with the probabilities 
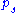of those states.
W.r.t. these different types of averaging, i.e. to distinguish pure and/or mixed states, one often uses the expressions 'coherent' and/or 'incoherent superposition' of quantum states.
For a discussion of conceptual aspects and a comparison with classical states, see:
For a more detailed coverage of mathematical aspects, see: In particular, see Sec. 2.3.
For a discussion of purifications of mixed quantum states, see Chapter 2 of John Preskill's lecture notes for Physics 219 at Caltech.
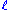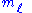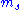, , , } defines the state of an electron within a hydrogen atom and are known as the electron's quantum numberQuantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s. Other examples could be "given direction and energy, or some other given condition", when we are talking about scattering. More generally, the state of the system is represented by a single vector known as a ket
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
.
Typically, one postulates some experimental apparatus and procedure which "prepares" this quantum state; the mathematical object reflects the setup of the apparatus. Quantum states can be either pure or mixed. Pure states cannot be described as a mixture of others. Mixed states correspond to an experiment involving a random process that blends pure states together.
When performing a particular measurement
Measurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
on a quantum state, the result is usually described by a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, and the form that this distribution takes is completely determined by the quantum state and the observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
describing the measurement. These probability distributions are necessary for both mixed states and pure states: It is impossible in quantum mechanics (unlike classical mechanics) to have any state whose properties are all fixed and certain. This is exemplified by the Heisenberg uncertainty principle, and reflects a core difference between classical
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
and quantum physics.
Mathematically, a pure quantum state is typically represented by a vector in a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
which is a generalization of our more usual three dimensional space. In a Hilbert space the co-ordinates are complex numbers, a complex kind of distance between points is defined and infinite series of numbers are made to converge. In physics, bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
is often used to denote such vectors. Linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s (superpositions
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
) of vectors can describe interference phenomena. Mixed quantum states are described by density matrices
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
.
In a more general mathematical context, quantum states can be understood as positive normalized linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s on a C* algebra; see GNS construction.
The state of a physical system
The state of a physical systemPhysical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
is a complete description of the parameters of the experiment.
To understand this rather abstract notion, it is useful to first explore it in an example from classical mechanics.
Consider an experiment with a (non-quantum) particle of mass
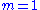that moves freely, and without friction, in one spatial direction.We put the particle at initial position
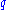and start the experiment at time by pushing the particle with some speed and in some direction. Doing this, we determine the initial momentumMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
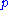
of the particle. These initial conditions are what characterizes the state
of the system,formally denoted as
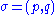. We say that we prepare the state of the systemby fixing its initial conditions.
At a later time
, we conduct measurements on the particle.The measurements we can perform on this simple
system are essentially its position
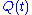at time , its momentum 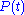,and combinations of these.
Here
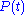and 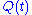refer to the measurable quantities (observables)of the system as such, not the specific results they produce in a certain run of the experiment.
However, knowing the state
of the system, we can compute thevalue of the observables in the specific state, i.e. the results that our measurements will produce,
depending on
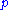and 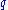.We denote these values as
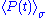and 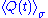.In our simple example, it is well known that the particle moves with constant velocity; therefore,
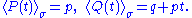
Now suppose that we start the particle with a random initial position and momentum.
(For argument's sake, we may suppose that the particle is pushed away at
by some apparatus which is controlled by a random number generator.)
The state
of the system is now not described by two numbers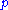 and 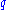, but rather by two probability distributions.The observables
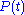and 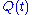will produce random results now;they become random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, and their values in a single measurement cannot be predicted.
However, if we repeat the experiment sufficiently often,
always preparing the same state
, we can predict the expectation valueof the observables (their statistical mean
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
) in the state
. The expectationvalue of
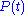is again denoted by 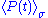, etc.These "statistical" states of the system are called mixed states,
as opposed to the pure states
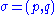discussed further below.Abstractly, mixed states arise as a statistical mixture
Mixture density
In probability and statistics, a mixture distribution is the probability distribution of a random variable whose values can be interpreted as being derived in a simple way from an underlying set of other random variables. In particular, the final outcome value is selected at random from among the...
of pure states.
Quantum states
The state
of the system is fixed by the way the physicist prepares the experiment(e.g., how the physicist adjusts the particle source). As above, there is a distinction between pure states and
mixed states, the latter being statistical mixtures of the former.
However, some important differences arise in comparison with classical mechanics.
In quantum theory, even pure states show statistical behaviour.
Regardless of how carefully we prepare the state
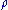of the system,measurement results are not repeatable in general, and we must understand the expectation value
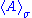of an observable 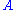as a statistical mean.It is this mean that is predicted by physical theories.
For any fixed observable
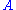, it is generallypossible to prepare a pure state
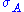such that 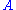has a fixedvalue in this state: If we repeat the experiment several times, each time
measuring
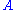, we will always obtain the same measurement result,without any random behaviour.
Such pure states
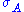are called eigenstates of 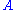.However, it is impossible to prepare a simultaneous eigenstate
for all observables. For example, we cannot prepare a state
such that both the position measurement
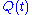
and the momentum measurement
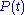
(at the same time
) produce "sharp" results;at least one of them will exhibit random behaviour.
This is the content of the Heisenberg uncertainty relation
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
.
Moreover, in contrast to classical mechanics, it is unavoidable that
performing a measurement on the system generally changes its state.
More precisely: After measuring an observable
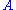,the system will be in an eigenstate of
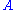; thus the state has changed, unless the system was already in that eigenstate.This expresses a kind of logical consistency: If we measure
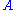twice in the samerun of the experiment, the measurements being directly consecutive in time, then they will
produce the same results. This has some strange consequences however:
Consider two observables,
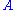and 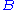, where 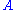correspondsto a measurement earlier in time than
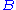.Suppose that the system is in an eigenstate of
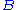.If we measure only
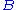, we will not notice statistical behaviour.If we measure first
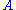and then 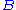in the same run of the experiment,the system will transfer to an eigenstate of
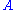after the first measurement,and we will generally notice that the results of
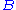are statistical.Thus, quantum mechanical measurements influence one another, and it is important
in which order they are performed.
Another feature of quantum states becomes relevant if we consider a physical system that
consists of multiple subsystems; for example, an experiment with two particles rather than one.
Quantum physics allows for certain states, called entangled states,
that show certain statistical correlations between measurements on the two particles
which cannot be explained by classical theory. For details, see entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
.
These entangled states lead to experimentally testable properties (Bell's theorem
Bell's theorem
In theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
)
that allow us to distinguish between quantum theory and alternative classical (non-quantum) models.
Schrödinger picture vs. Heisenberg picture
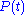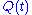
In the discussion above, we have taken the observables, to be dependent on time, while the state
was fixed once at the beginning of the experiment.This approach is called the Heisenberg picture
Heisenberg picture
In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
. One can, equivalently, treat the observables as fixed,
while the state of the system depends on time; that is known as the Schrödinger picture
Schrödinger picture
In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...
.
Conceptually (and mathematically), both approaches are equivalent; choosing one of them is a matter of convention.
Both viewpoints are used in quantum theory. While non-relativistic quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
is usually formulated
in terms of the Schrödinger picture, the Heisenberg picture is often preferred in a relativistic context,
that is, for quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
Compare with Dirac picture.
Pure states as rays in a Hilbert space
Quantum physics is most commonly formulated in terms of linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, as follows. Any given system is identified with some Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, such that each vector in the Hilbert space (apart from the origin) corresponds to a pure quantum state. In addition, two vectors that differ only by a nonzero complex scalar
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
correspond to the same state (in other words, each pure state is a ray in the Hilbert space; equivalently, a point in the projective Hilbert space
Projective Hilbert space
In mathematics and the foundations of quantum mechanics, the projective Hilbert space P of a complex Hilbert space H is the set of equivalence classes of vectors v in H, with v ≠ 0, for the relation given by...
.).
Alternatively, many authors choose to only consider normalized vectors (vectors of norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
1) as corresponding to quantum states. In this case, the set of all pure states corresponds to the unit sphere
Unit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
of a Hilbert space, with the proviso that two normalized vectors correspond to the same state if they differ only by a complex scalar of absolute value 1, which is called the phase factor.
Bra-ket notation
Calculations in quantum mechanics make frequent use of linear operators, inner products, dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
s, and Hermitian conjugation. In order to make such calculations more straightforward, and to obviate the need (in some contexts) to fully understand the underlying linear algebra, Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
invented a notation to describe quantum states, known as bra-ket notation. Although the details of this are beyond the scope of this article (see the article Bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
), some consequences of this are:
- The variable name used to denote a vector (which corresponds to a pure quantum state) is chosen to be of the form
(where the "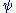
" can be replaced by any other symbols, letters, numbers, or even words). This can be contrasted with the usual mathematical notation, where vectors are usually bold, lower-case letters, or letters with arrows on top. - Instead of vector, the term ket is used synonymously.
- Each ket
is uniquely associated with a so-called bra, denoted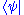 
, which is also said to correspond to the same physical quantum state. Technically, the bra is an element of the dual space, and related to the ket by the Riesz representation theoremRiesz representation theoremThere are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
. - Inner products (also called brackets) are written so as to look like a bra and ket next to each other:
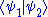. (Note that the phrase "bra-ket" is supposed to resemble "bracket".)
Spin, many-body states
It is important to note that in quantum mechanics besides, e.g., the usual position variable, a discrete variable m exists, corresponding to the value of the z-component of the spinSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
vector. This can be thought of as a kind of intrinsic angular momentum. However, it does not appear at all in classical mechanics and arises from Dirac's relativistic generalization of the theory. As a consequence, the quantum state of a system of N particles is described by a function with four variables per particle, e.g.
. Here, the variables mν assume values from the set {}, where 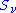(in units of Planck's reduced constant 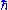), is either a non-negative integer (0,1,2...; bosonBoson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s), or semi-integer (1/2,3/2,5/2,...; fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s). Moreover, in the case of identical particles, the above N-particle function must either be symmetrized (in the bosonic case) or anti-symmetrized (in the fermionic case) with respect to the particle numbers.
Electrons are fermions with S = 1/2, photons (quanta of light) are bosons with S = 1.
Apart from the symmetrization or anti-symmetrization, N-particle states can thus simply be obtained by tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of one-particle states, to which we return herewith.
Basis states of one-particle systems
As with any vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, if a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
is chosen for the Hilbert space of a system, then any ket can be expanded as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of those basis elements. Symbolically, given basis kets
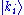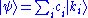
, any ket can be writtenwhere ci are complex numbers. In physical terms, this is described by saying that
has been expressed as a quantum superposition of the states 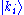. If the basis kets are chosen to be orthonormalOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
(as is often the case), then
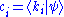.One property worth noting is that the normalized states
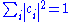
are characterized byExpansions of this sort play an important role in measurement in quantum mechanics. In particular, if the
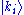are eigenstates (with eigenvalues 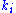) of an observable, and that observable is measured on the normalized state , then the probability that the result of the measurement is ki is |ci|2. (The normalization condition above mandates that the total sum of probabilities is equal to one.)A particularly important example is the position basis, which is the basis consisting of eigenstates of the observable which corresponds to measuring position. If these eigenstates are nondegenerate (for example, if the system is a single, spinless
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
particle), then any ket
is associated with a complex-valued function of three-dimensional space:.This function is called the wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
corresponding to
.Superposition of pure states
One aspect of quantum states, mentioned above, is that superpositionsSuperposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of them can be formed. If
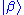and are two kets corresponding to quantum states, the ket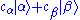is a different quantum state (possibly not normalized). Note that which quantum state it is depends on both the amplitudes and phases (arguments) of
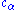and 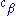. In other words, for example, even though and 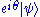(for real θ) correspond to the same physical quantum state, they are not interchangeable, since for example and 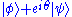do not (in general) correspond to the same physical state. However, and 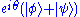do correspond to the same physical state. This is sometimes described by saying that "global" phase factors are unphysical, but "relative" phase factors are physical and important.One example of a quantum interference phenomenon that arises from superposition is the double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
. The photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
state is a superposition of two different states, one of which corresponds to the photon having passed through the left slit, and the other corresponding to passage through the right slit. The relative phase of those two states has a value which depends on the distance from each of the two slits. Depending on what that phase is, the interference is constructive at some locations and destructive in others, creating the interference pattern.
Another example of the importance of relative phase in quantum superposition is Rabi oscillations, where the relative phase of two states varies in time due to the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. The resulting superposition ends up oscillating back and forth between two different states.
Mixed states
A pure quantum state is a state which can be described by a single ket vector, as described above. A mixed quantum state is a statistical ensemble of pure states (see quantum statistical mechanicsQuantum statistical mechanics
Quantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be...
). Equivalently, a mixed-quantum state on a given quantum system described by a Hilbert space H naturally arises as a pure quantum state (called a purification) on a larger bipartite system H tensor K, the other half of which is inaccessible to the observer.
A mixed state cannot be described as a ket vector. Instead, it is described by its associated density matrix (or density operator), usually denoted
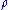. Note that density matrices can describe both mixed and pure states, treating them on the same footing.The density matrix is defined as
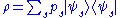
where
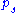is the fraction of the ensemble in each pure state 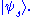Here, one typically uses a one-particle formalism to describe the average behaviour of an N-particle system.A simple criterion for checking whether a density matrix is describing a pure or mixed state is that the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of ρ2 is equal to 1 if the state is pure, and less than 1 if the state is mixed. Another, equivalent, criterion is that the von Neumann entropy
Von Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
is 0 for a pure state, and strictly positive for a mixed state.
The rules for measurement in quantum mechanics are particularly simple to state in terms of density matrices. For example, the ensemble average (expectation value
Expectation value (quantum mechanics)
In quantum mechanics, the expectation value is the predicted mean value of the result of an experiment. Despite the name, it is not the most probable value of a measurement...
) of a measurement corresponding to an observable
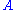is given by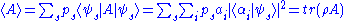where
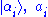are eigenkets and eigenvalues, respectively, for the operator 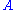, and tr denotes trace. It is important to note that two types of averaging are occurring, one being a quantum average over the basis kets 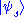of the pure states, and the other being a statistical average with the probabilities 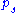of those states.W.r.t. these different types of averaging, i.e. to distinguish pure and/or mixed states, one often uses the expressions 'coherent' and/or 'incoherent superposition' of quantum states.
Mathematical formulation
For a mathematical discussion on states as functionals, see Gelfand–Naimark–Segal construction. There, the same objects are described in a C*-algebraic context.See also
- Basic concepts of quantum mechanicsBasic concepts of quantum mechanicsQuantum mechanics explains the behaviour of matter and energy on the scale of atoms and subatomic particles.Classical physics explains matter and energy at the macroscopic level of the scale familiar to human experience, including the behavior of astronomical bodies...
- Excited stateExcited stateExcitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being excited to an excited state....
- Introduction to quantum mechanicsIntroduction to quantum mechanicsQuantum mechanics is the body of scientific principles that explains the behavior of matter and its interactions with energy on the scale of atoms and atomic particles....
- Orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
- Probability amplitudeProbability amplitudeIn quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
- Quantum harmonic oscillatorQuantum harmonic oscillatorThe quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
- QubitQubitIn quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
- Stationary stateStationary stateIn quantum mechanics, a stationary state is an eigenvector of the Hamiltonian, implying the probability density associated with the wavefunction is independent of time . This corresponds to a quantum state with a single definite energy...
- W stateW stateThe W state is an entangled quantum state of three qubits which has the following shapeand which is remarkable for representing a specific type of multipartite entanglement and for occurring in several applications in quantum information theory.-Properties:...
- Wave function
Further reading
The concept of quantum states, in particular the content of the section Formalism in quantum physics above, is covered in most standard textbooks on quantum mechanics.For a discussion of conceptual aspects and a comparison with classical states, see:
For a more detailed coverage of mathematical aspects, see: In particular, see Sec. 2.3.
For a discussion of purifications of mixed quantum states, see Chapter 2 of John Preskill's lecture notes for Physics 219 at Caltech.