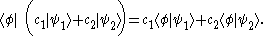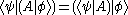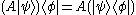Bra-ket notation
Encyclopedia
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics
composed of angle brackets
and vertical bar
s. It can also be used to denote abstract vectors
and linear functional
s in mathematics
. It is so called because the inner product (or dot product
) of two states is denoted by a bracket,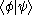 , consisting of a left part,
, consisting of a left part, 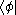 , called the bra (ˈbrɑː), and a right part,
, called the bra (ˈbrɑː), and a right part, 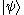 , called the ket (ˈkɛt). The notation was introduced in 1930 by Paul Dirac
, called the ket (ˈkɛt). The notation was introduced in 1930 by Paul Dirac
, and is also known as Dirac notation.
Bra-ket notation is widespread in quantum mechanics
: almost every phenomenon that is explained using quantum mechanics—including a large portion of modern physics
—is usually explained with the help of bra-ket notation. The expression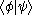 is typically interpreted as the probability amplitude
is typically interpreted as the probability amplitude
for the state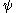 to collapse
to collapse
into the state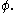
, the state of a physical
system is identified with a ray in a complex
separable Hilbert space
,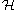 , or, equivalently, by a point in the projective Hilbert space
, or, equivalently, by a point in the projective Hilbert space
of the system. Each vector
in the ray is called a "ket" and written as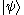 , which would be read as "ket psi
, which would be read as "ket psi
". (The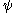 can be replaced by any symbols, letters, numbers, or even words—whatever serves as a convenient label for the ket.)
can be replaced by any symbols, letters, numbers, or even words—whatever serves as a convenient label for the ket.)
The ket can be viewed as a column vector and (given a basis for the Hilbert space) written out in coordinates,
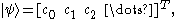
when the considered Hilbert space is finite-dimensional. In infinite-dimensional spaces there are infinitely many coordinates and the ket may be written in complex function notation, by prepending it with a bra (see below). For example,
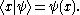
Every ket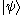 has a dual bra, written as
has a dual bra, written as 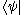 . For example, the bra corresponding to the ket
. For example, the bra corresponding to the ket 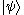 above would be the row vector
above would be the row vector
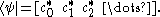
This is a continuous linear functional
from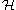 to the complex numbers
to the complex numbers 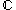 , defined by:
, defined by:
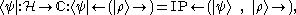
for all kets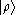 , where
, where 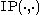 denotes the inner product defined on the Hilbert space
denotes the inner product defined on the Hilbert space
. Here the origin of the bra-ket notation becomes clear: when we drop the parentheses (as is common with linear functionals) and meld the bars together we get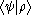 , which is common notation for an inner product in a Hilbert space. This combination of a bra with a ket to form a complex number is called a bra-ket or bracket.
, which is common notation for an inner product in a Hilbert space. This combination of a bra with a ket to form a complex number is called a bra-ket or bracket.
The bra is simply the conjugate transpose
(also called the Hermitian conjugate) of the ket and vice versa. The notation is justified by the Riesz representation theorem
, which states that a Hilbert space and its dual space
are isometrically conjugate isomorphic. Thus, each bra corresponds to exactly one ket, and vice versa. More precisely, if
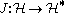
is the Riesz isomorphism between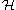 and its dual space, then
and its dual space, then
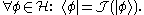
Note that this only applies to states that are actually vectors in the Hilbert space. Non-normalizable states, such as those whose wavefunction
s are Dirac delta function
s or infinite plane wave
s, do not technically belong to the Hilbert space. So if such a state is written as a ket, it will not have a corresponding bra according to the above definition. This problem can be dealt with in either of two ways. First, since all physical quantum states are normalizable, one can carefully avoid non-normalizable states. Alternatively, the underlying theory can be modified and generalized to accommodate such states, as in the Gelfand–Naimark–Segal construction or rigged Hilbert space
s. In fact, physicists routinely use bra-ket notation for non-normalizable states, taking the second approach either implicitly or explicitly.
In quantum mechanics the expression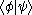 (mathematically: the coefficient for the projection of
(mathematically: the coefficient for the projection of 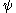 onto
onto 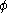 ) is typically interpreted as the probability amplitude
) is typically interpreted as the probability amplitude
for the state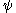 to collapse
to collapse
into the state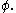
The advantage of the bra-ket notation over explicit wave function algebra is the possibility of expressing operations on quantum states independent of a basis. For example the time-independent Schrödinger equation
is simply expressed as
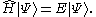
The operators can be conveniently expressed in different bases (see next section for the operations used in these formulas : action of a linear operator, outer product of a ket and a bra):
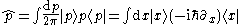
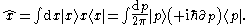
(For a rigorous definition of basis with a continuous set of indices and consequently for a rigorous definition of position and momentum basis see )
(For a rigorous statement of the expansion of an S-diagonalizable operator - observable - in its eigenbasis or in another basis see )
The wave functions in real, momentum or reciprocal space can be retrieved as needed: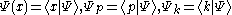
and all basis conversions can be performed via the relations such as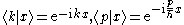
(for a rigorous treatment of the Dirac inner product of non-normalizable states see the definition given by D. Carfì in and )
. In any Banach space
B, the vectors may be notated by kets and the continuous linear functional
s by bras. Over any vector space without topology
, we may also notate the vectors by kets and the linear functionals by bras. In these more general contexts, the bracket does not have the meaning of an inner product, because the Riesz representation theorem does not apply.
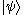 to obtain the ket
to obtain the ket 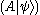 . Linear operators are ubiquitous in the theory of quantum mechanics. For example, observable physical quantities are represented by self-adjoint operator
. Linear operators are ubiquitous in the theory of quantum mechanics. For example, observable physical quantities are represented by self-adjoint operator
s, such as energy
or momentum
, whereas transformative processes are represented by unitary
linear operators such as rotation or the progression of time.
Operators can also be viewed as acting on bras from the right hand side. Composing the bra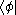 with the operator A results in the bra
with the operator A results in the bra 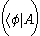 , defined as a linear functional on H by the rule
, defined as a linear functional on H by the rule
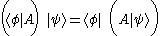 .
.
This expression is commonly written as (cf. energy inner product)
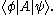
Note that the second symbol | is completely optional, i.e.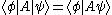 , since
, since 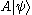 is in itself a ket and may be written
is in itself a ket and may be written 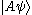 .
.
If the same state vector appears on both bra and ket side, this expression gives the expectation value
, or mean or average value, of the observable represented by operator A for the physical system in the state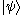 , written as
, written as
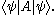
A convenient way to define linear operators on H is given by the outer product
: if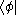 is a bra and
is a bra and 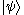 is a ket, the outer product
is a ket, the outer product
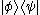
denotes the rank-one operator that maps the ket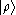 to the ket
to the ket 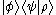 (where
(where 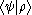 is a scalar multiplying the vector
is a scalar multiplying the vector 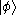 ). One of the uses of the outer product is to construct projection operators. Given a ket
). One of the uses of the outer product is to construct projection operators. Given a ket 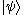 of norm 1, the orthogonal projection onto the subspace
of norm 1, the orthogonal projection onto the subspace
spanned by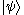 is
is
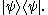
Just as kets and bras can be transformed into each other (making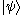 into
into 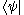 ) the element from the dual space corresponding with
) the element from the dual space corresponding with 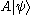 is
is 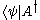 where A† denotes the Hermitian conjugate (or adjoint) of the operator A.
where A† denotes the Hermitian conjugate (or adjoint) of the operator A.
It is usually taken as a postulate or axiom
of quantum mechanics
, that any operator corresponding to an observable
quantity
(shortly called observable) is self-adjoint, that is, it satisfies A† = A. Then the identity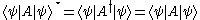
holds (for the first equality, use the scalar product's conjugate symmetry
and the conversion rule from the
preceding paragraph).
This implies that expectation values
of observables are real.
s, c* denotes the complex conjugate
of c, A and B denote arbitrary linear operators, and these properties are to hold for any choice of bras and kets.
and so forth. The expressions can thus be written, unambiguously, with no parentheses whatsoever. Note that the associative property does not hold for expressions that include non-linear operators, such as the antilinear time reversal operator
in physics.
These rules are sufficient to formally write the Hermitian conjugate of any such expression; some examples are as follows:
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
composed of angle brackets
Bracket
Brackets are tall punctuation marks used in matched pairs within text, to set apart or interject other text. In the United States, "bracket" usually refers specifically to the "square" or "box" type.-List of types:...
and vertical bar
Vertical bar
The vertical bar is a character with various uses in mathematics, where it can be used to represent absolute value, among others; in computing and programming and in general typography, as a divider not unlike the interpunct...
s. It can also be used to denote abstract vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
and linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. It is so called because the inner product (or dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
) of two states is denoted by a bracket,
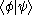 , consisting of a left part,
, consisting of a left part, 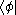 , called the bra (ˈbrɑː), and a right part,
, called the bra (ˈbrɑː), and a right part, 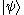 , called the ket (ˈkɛt). The notation was introduced in 1930 by Paul Dirac
, called the ket (ˈkɛt). The notation was introduced in 1930 by Paul DiracPaul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, and is also known as Dirac notation.
Bra-ket notation is widespread in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
: almost every phenomenon that is explained using quantum mechanics—including a large portion of modern physics
Modern physics
The term modern physics refers to the post-Newtonian conception of physics. The term implies that classical descriptions of phenomena are lacking, and that an accurate, "modern", description of reality requires theories to incorporate elements of quantum mechanics or Einsteinian relativity, or both...
—is usually explained with the help of bra-ket notation. The expression
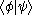 is typically interpreted as the probability amplitude
is typically interpreted as the probability amplitudeProbability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
for the state
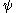 to collapse
to collapseWavefunction collapse
In quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer...
into the state
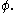
Usage in quantum mechanics
In quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the state of a physical
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
system is identified with a ray in a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
separable Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
,
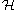 , or, equivalently, by a point in the projective Hilbert space
, or, equivalently, by a point in the projective Hilbert spaceProjective Hilbert space
In mathematics and the foundations of quantum mechanics, the projective Hilbert space P of a complex Hilbert space H is the set of equivalence classes of vectors v in H, with v ≠ 0, for the relation given by...
of the system. Each vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
in the ray is called a "ket" and written as
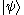 , which would be read as "ket psi
, which would be read as "ket psiPsi (letter)
Psi is the 23rd letter of the Greek alphabet and has a numeric value of 700. In both Classical and Modern Greek, the letter indicates the combination /ps/ . The letter was adopted into the Old Italic alphabet, and its shape is continued into the Algiz rune of the Elder Futhark...
". (The
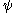 can be replaced by any symbols, letters, numbers, or even words—whatever serves as a convenient label for the ket.)
can be replaced by any symbols, letters, numbers, or even words—whatever serves as a convenient label for the ket.)The ket can be viewed as a column vector and (given a basis for the Hilbert space) written out in coordinates,
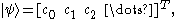
when the considered Hilbert space is finite-dimensional. In infinite-dimensional spaces there are infinitely many coordinates and the ket may be written in complex function notation, by prepending it with a bra (see below). For example,
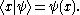
Every ket
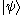 has a dual bra, written as
has a dual bra, written as 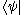 . For example, the bra corresponding to the ket
. For example, the bra corresponding to the ket 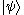 above would be the row vector
above would be the row vector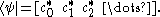
This is a continuous linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
from
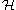 to the complex numbers
to the complex numbers 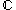 , defined by:
, defined by: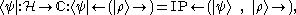
for all kets
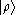 , where
, where 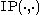 denotes the inner product defined on the Hilbert space
denotes the inner product defined on the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. Here the origin of the bra-ket notation becomes clear: when we drop the parentheses (as is common with linear functionals) and meld the bars together we get
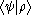 , which is common notation for an inner product in a Hilbert space. This combination of a bra with a ket to form a complex number is called a bra-ket or bracket.
, which is common notation for an inner product in a Hilbert space. This combination of a bra with a ket to form a complex number is called a bra-ket or bracket.The bra is simply the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
(also called the Hermitian conjugate) of the ket and vice versa. The notation is justified by the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, which states that a Hilbert space and its dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
are isometrically conjugate isomorphic. Thus, each bra corresponds to exactly one ket, and vice versa. More precisely, if
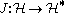
is the Riesz isomorphism between
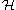 and its dual space, then
and its dual space, then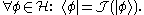
Note that this only applies to states that are actually vectors in the Hilbert space. Non-normalizable states, such as those whose wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s are Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
s or infinite plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
s, do not technically belong to the Hilbert space. So if such a state is written as a ket, it will not have a corresponding bra according to the above definition. This problem can be dealt with in either of two ways. First, since all physical quantum states are normalizable, one can carefully avoid non-normalizable states. Alternatively, the underlying theory can be modified and generalized to accommodate such states, as in the Gelfand–Naimark–Segal construction or rigged Hilbert space
Rigged Hilbert space
In mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
s. In fact, physicists routinely use bra-ket notation for non-normalizable states, taking the second approach either implicitly or explicitly.
In quantum mechanics the expression
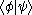 (mathematically: the coefficient for the projection of
(mathematically: the coefficient for the projection of 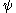 onto
onto 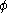 ) is typically interpreted as the probability amplitude
) is typically interpreted as the probability amplitudeProbability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
for the state
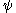 to collapse
to collapseWavefunction collapse
In quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer...
into the state
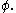
The advantage of the bra-ket notation over explicit wave function algebra is the possibility of expressing operations on quantum states independent of a basis. For example the time-independent Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
is simply expressed as
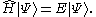
The operators can be conveniently expressed in different bases (see next section for the operations used in these formulas : action of a linear operator, outer product of a ket and a bra):
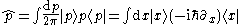
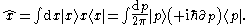
(For a rigorous definition of basis with a continuous set of indices and consequently for a rigorous definition of position and momentum basis see )
(For a rigorous statement of the expansion of an S-diagonalizable operator - observable - in its eigenbasis or in another basis see )
The wave functions in real, momentum or reciprocal space can be retrieved as needed:
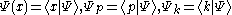
and all basis conversions can be performed via the relations such as
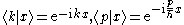
(for a rigorous treatment of the Dirac inner product of non-normalizable states see the definition given by D. Carfì in and )
More general uses
Bra-ket notation can be used even if the vector space is not a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. In any Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
B, the vectors may be notated by kets and the continuous linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s by bras. Over any vector space without topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, we may also notate the vectors by kets and the linear functionals by bras. In these more general contexts, the bracket does not have the meaning of an inner product, because the Riesz representation theorem does not apply.
Linear operators
If A : H → H is a linear operator, we can apply A to the ket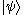 to obtain the ket
to obtain the ket 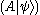 . Linear operators are ubiquitous in the theory of quantum mechanics. For example, observable physical quantities are represented by self-adjoint operator
. Linear operators are ubiquitous in the theory of quantum mechanics. For example, observable physical quantities are represented by self-adjoint operatorSelf-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s, such as energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
or momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, whereas transformative processes are represented by unitary
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
linear operators such as rotation or the progression of time.
Operators can also be viewed as acting on bras from the right hand side. Composing the bra
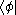 with the operator A results in the bra
with the operator A results in the bra 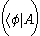 , defined as a linear functional on H by the rule
, defined as a linear functional on H by the rule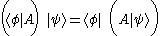 .
.This expression is commonly written as (cf. energy inner product)
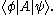
Note that the second symbol | is completely optional, i.e.
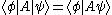 , since
, since 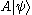 is in itself a ket and may be written
is in itself a ket and may be written 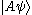 .
.If the same state vector appears on both bra and ket side, this expression gives the expectation value
Expectation value (quantum mechanics)
In quantum mechanics, the expectation value is the predicted mean value of the result of an experiment. Despite the name, it is not the most probable value of a measurement...
, or mean or average value, of the observable represented by operator A for the physical system in the state
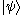 , written as
, written as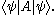
A convenient way to define linear operators on H is given by the outer product
Outer product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
: if
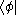 is a bra and
is a bra and 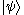 is a ket, the outer product
is a ket, the outer product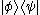
denotes the rank-one operator that maps the ket
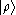 to the ket
to the ket 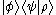 (where
(where 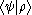 is a scalar multiplying the vector
is a scalar multiplying the vector 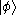 ). One of the uses of the outer product is to construct projection operators. Given a ket
). One of the uses of the outer product is to construct projection operators. Given a ket 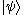 of norm 1, the orthogonal projection onto the subspace
of norm 1, the orthogonal projection onto the subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
spanned by
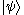 is
is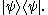
Just as kets and bras can be transformed into each other (making
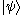 into
into 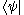 ) the element from the dual space corresponding with
) the element from the dual space corresponding with 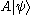 is
is 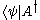 where A† denotes the Hermitian conjugate (or adjoint) of the operator A.
where A† denotes the Hermitian conjugate (or adjoint) of the operator A.It is usually taken as a postulate or axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, that any operator corresponding to an observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
quantity
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
(shortly called observable) is self-adjoint, that is, it satisfies A† = A. Then the identity
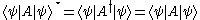
holds (for the first equality, use the scalar product's conjugate symmetry
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
and the conversion rule from the
preceding paragraph).
This implies that expectation values
Expectation value (quantum mechanics)
In quantum mechanics, the expectation value is the predicted mean value of the result of an experiment. Despite the name, it is not the most probable value of a measurement...
of observables are real.
Properties
Bra-ket notation was designed to facilitate the formal manipulation of linear-algebraic expressions. Some of the properties that allow this manipulation are listed herein. In what follows, c1 and c2 denote arbitrary complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, c* denotes the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of c, A and B denote arbitrary linear operators, and these properties are to hold for any choice of bras and kets.
Linearity
- Since bras are linear functionals,
- By the definition of addition and scalar multiplication of linear functionals in the dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
,
Associativity
Given any expression involving complex numbers, bras, kets, inner products, outer products, and/or linear operators (but not addition), written in bra-ket notation, the parenthetical groupings do not matter (i.e., the associative property holds). For example:and so forth. The expressions can thus be written, unambiguously, with no parentheses whatsoever. Note that the associative property does not hold for expressions that include non-linear operators, such as the antilinear time reversal operator
T-symmetry
T Symmetry is the symmetry of physical laws under a time reversal transformation: T: t \mapsto -t.Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.Time asymmetries...
in physics.
Hermitian conjugation
Bra-ket notation makes it particularly easy to compute the Hermitian conjugate (also called dagger, and denoted †) of expressions. The formal rules are:- The Hermitian conjugate of a bra is the corresponding ket, and vice-versa.
- The Hermitian conjugate of a complex number is its complex conjugate.
- The Hermitian conjugate of the Hermitian conjugate of anything (linear operators, bras, kets, numbers) is itself—i.e.,
-
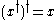 .
.
- Given any combination of complex numbers, bras, kets, inner products, outer products, and/or linear operators, written in bra-ket notation, its Hermitian conjugate can be computed by reversing the order of the components, and taking the Hermitian conjugate of each.
These rules are sufficient to formally write the Hermitian conjugate of any such expression; some examples are as follows:
- Kets:
-
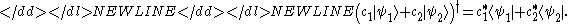
- Inner products:
-
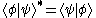
- Matrix elements:
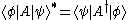

- Outer products:

Composite bras and kets
Two Hilbert spaces V and W may form a third space by a tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
by a tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
. In quantum mechanics, this is used for describing composite systems. If a system is composed of two subsystems described in V and W respectively, then the Hilbert space of the entire system is the tensor product of the two spaces. (The exception to this is if the subsystems are actually identical particlesIdentical particlesIdentical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
. In that case, the situation is a little more complicated.)
If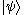 is a ket in V and
is a ket in V and 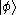 is a ket in W, the direct product of the two kets is a ket in
is a ket in W, the direct product of the two kets is a ket in  . This is written variously as
. This is written variously as
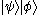 or
or 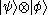 or
or 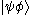 or
or 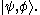
Representations in terms of bras and kets
In quantum mechanics, it is often convenient to work with the projections of state vectors onto a particular basis, rather than the vectors themselves. The reason is that the former are simply complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, and can be formulated in terms of partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s (see, for example, the derivation of the position-basis Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
). This process is very similar to the use of coordinate vectors in linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
.
For instance, the Hilbert space of a zero-spinSpin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
point particle is spanned by a position basis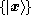 , where the label x extends over the set of position vectors. Starting from any ket
, where the label x extends over the set of position vectors. Starting from any ket 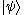 in this Hilbert space, we can define a complex scalar function of x, known as a wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
in this Hilbert space, we can define a complex scalar function of x, known as a wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
:
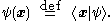
It is then customary to define linear operators acting on wavefunctions in terms of linear operators acting on kets, by
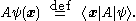
For instance, the momentumMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
operator p has the following form:
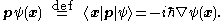
One occasionally encounters an expression like
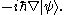
This is something of an abuse of notationAbuse of notationIn mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
, though a fairly common one. The differential operator must be understood to be an abstract operator, acting on kets, that has the effect of differentiating wavefunctions once the expression is projected into the position basis:
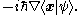
For further details, see rigged Hilbert spaceRigged Hilbert spaceIn mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
.
The unit operator
Consider a complete orthonormal system (basisBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
),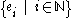 , for a Hilbert space H, with respect to the norm from an inner product
, for a Hilbert space H, with respect to the norm from an inner product 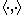 . From basic functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. From basic functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
we know that any ket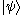 can be written as
can be written as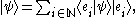
with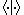 the inner product on the Hilbert space. From the commutativity of kets with (complex) scalars now follows that
the inner product on the Hilbert space. From the commutativity of kets with (complex) scalars now follows that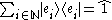
must be the unit operator, which sends each vector to itself. This can be inserted in any expression without affecting its value, for example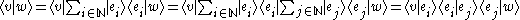
where in the last identity Einstein summation convention has been used.
In quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
it often occurs that little or no information about the inner product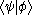 of two arbitrary (state) kets is present, while it is possible to say something about the expansion coefficients
of two arbitrary (state) kets is present, while it is possible to say something about the expansion coefficients 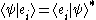 and
and  of those vectors with respect to a chosen (orthonormalized) basis. In this case it is particularly useful to insert the unit operator into the bracket one time or more (for more information see Resolution of the identity).
of those vectors with respect to a chosen (orthonormalized) basis. In this case it is particularly useful to insert the unit operator into the bracket one time or more (for more information see Resolution of the identity).
Notation used by mathematicians
The object physicists are considering when using the "bra-ket" notation is a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
(a complete inner product spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
).
Let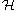 be a Hilbert space and
be a Hilbert space and  is a vector in
is a vector in  . What physicists would denote as
. What physicists would denote as 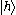 is the vector itself. That is
is the vector itself. That is
-
 .
.
Let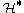 be the dual space of
be the dual space of 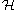 . This is the space of linear functionals on
. This is the space of linear functionals on 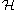 . The isomorphism
. The isomorphism 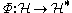 is defined by
is defined by 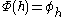 where for all
where for all 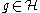 we have
we have
-
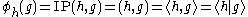 ,
,
Where
are just different notations for expressing an inner product between two elements in a Hilbert space (or for the first three, in any inner product space). Notational confusion arises when identifying and
and 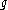 with
with 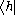 and
and  respectively. This is because of literal symbolic substitutions. Let
respectively. This is because of literal symbolic substitutions. Let 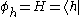 and let
and let 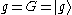 . This gives
. This gives
-
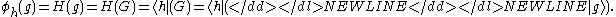
One ignores the parentheses and removes the double bars. Some properties of this notation are convenient since we are dealing with linear operators and composition acts like a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
multiplication.
External links
- Richard Fitzpatrick, "Quantum Mechanics: A graduate level course", The University of Texas at Austin.
- 1. Ket space
- 2. Bra space
- 3. Operators
- 4. The outer product
- 5. Eigenvalues and eigenvectors
- Robert Littlejohn, Lecture notes on "The Mathematical Formalism of Quantum mechanics", including bra-ket notation.
- Richard Fitzpatrick, "Quantum Mechanics: A graduate level course", The University of Texas at Austin.