Outer product
Encyclopedia
- For "outer product" in geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, see exterior productExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
.
In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the outer product typically refers to the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of two vectors. The result of applying the outer product to a pair of vectors is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. The name contrasts with the inner product, which takes as input a pair of vectors and produces a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
.
The outer product of vectors can be also regarded as a special case of the Kronecker product
Kronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
of matrices.
Some authors use the expression "outer product of tensors" as a synonym of "tensor product". The outer product is also a higher-order function
Higher-order function
In mathematics and computer science, higher-order functions, functional forms, or functionals are functions which do at least one of the following:*take one or more functions as an input*output a function...
in some computer programming languages such as APL
APL programming language
APL is an interactive array-oriented language and integrated development environment, which is available from a number of commercial and noncommercial vendors and for most computer platforms. It is based on a mathematical notation developed by Kenneth E...
and Mathematica
Mathematica
Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
.
Definition
Given a vector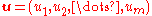
with m elements and a vector 
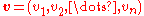with n elements, their outer product 
is defined as the 
matrix 
obtained by multiplying each element of 
by each element of 
:
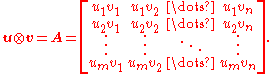
Note that
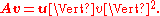
For complex vectors, it is customary to use the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of
(denoted 
). Namely, matrix 
is obtained by multiplying each element of 
by the complex conjugate of each element of 
.Definition (matrix multiplication)
The outer product
as defined above is equivalent to a matrix multiplication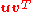 
, provided that 
is represented as a 
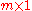column vector and 
as a 
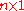column vector (which makes 
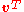a row vector). For instance, if 
and 
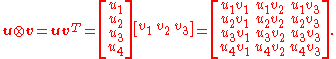
For complex vectors, it is customary to use the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of
(denoted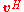 
):
Contrast with inner product
If m = n, then one can take the matrix product the other way, yielding a scalar (or
matrix):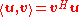
which is the standard inner product for Euclidean vector spaces, better known as the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
. The inner product is the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the outer product.
Definition (abstract)
Let V and W be two vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, and let W* be the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of W.
Given a vector x ∈ V and y* ∈ W*, then the tensor product y* ⊗ x corresponds to the map A : W → V given by
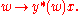
Here y*(w) denotes the value of the linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
y* (which is an element of the dual space of W) when evaluated at the element w ∈ W. This scalar in turn is multiplied by x to give as the final result an element of the space V.
Thus intrinsically, the outer product is defined for a vector and a covector; to define the outer product of two vectors requires converting one vector to a covector (in coordinates, transpose), which one can do in the presence of a bilinear form
generally taken to be a nondegenerate form (meaning this is an isomorphism) or more narrowly an inner product.If V and W are finite-dimensional, then the space of all linear transformations from W to V, denoted Hom(W,V), is generated by such outer products; in fact, the rank of a matrix is the minimal number of such outer products needed to express it as a sum (this is the tensor rank of a matrix). In this case Hom(W,V) is isomorphic to W* ⊗ V.
Contrast with inner product
If
, then one can also pair the covector w*∈V* with the vector v∈V via 
, which is the duality pairing between V and its dual, sometimes called the inner product.Definition (tensor multiplication)
The outer product on tensors is typically referred to as the tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
. Given a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
a with rank q and dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s (i 1, ..., i q), and a tensor b with rank r and dimensions (j 1, ..., j r), their outer product c has rank q+r and dimensions (k 1, ..., k q+r) which are the i dimensions followed by the j dimensions. For example, if A has rank 3 and dimensions (3, 5, 7) and B has rank 2 and dimensions (10, 100), their outer product c has rank 5 and dimensions (3, 5, 7, 10, 100). If A[2, 2, 4] = 11 and B[8, 88]= 13 then C[2, 2, 4, 8, 88] = 143. .
To understand the matrix definition of outer product in terms of the definition of tensor product:
- The vector v can be interpreted as a rank 1 tensor with dimension (M), and the vector u as a rank 1 tensor with dimension (N). The result is a rank 2 tensor with dimension (M, N).
- The rank of the result of an inner product between two tensors of rank q and r is the greater of q+r-2 and 0. Thus, the inner product of two matrices has the same rank as the outer product (or tensor product) of two vectors.
- It is possible to add arbitrarily many leading or trailing 1 dimensions to a tensor without fundamentally altering its structure. These 1 dimensions would alter the character of operations on these tensors, so any resulting equivalences should be expressed explicitly.
- The inner product of two matrices V with dimensions (d, e) and U with dimensions (e, f) is
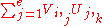where 
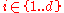and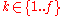 
, For the case where e =1, the summation is trivial (involving only a single term).
The term "rank" is used here in its tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
sense, and should not be interpreted as matrix rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
.
Applications
The outer product is useful in computing physical quantities (e.g., the tensor of inertiaMoment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
), and performing transform operations in digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
and digital image processing
Digital image processing
Digital image processing is the use of computer algorithms to perform image processing on digital images. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing...
. It is also useful in statistical analysis for computing the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
and auto-covariance matrices for two random variables.
Duality
- Complex conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
- Conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
- TransposeTransposeIn linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
- Bra-ket notationBra-ket notationBra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
for outer product