Geometric algebra
Encyclopedia
Geometric algebra together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry
. GA now finds application in all of physics
, in graphics
and in robotics
. GA is Clifford algebra
over the field of real numbers, where the naturally embedded Grassmann algebra
plays a part. Spacetime algebra
and Conformal Geometric algebra are specific examples of GA.
A feature of GA is its geometric interpretation due to the natural correspondence between geometric entities and the elements of the algebra. GA allows direct manipulation of subspaces and is a coordinate-free formalism. Proponents argue that it provides compact and intuitive descriptions in many areas including classical
and quantum mechanics
, electromagnetic theory and relativity
among others. In many cases, the "proliferation of manifolds" that occurs during the standard curriculum of differential geometry can be reduced by working with real-only algebras.
Given a finite dimensional real quadratic space with quadratic form , the geometric algebra for this quadratic space is the Clifford algebra
Cℓ(V,Q).
The algebra product is called the geometric product, and it is just the Clifford product. It is standard to denote the geometric product by juxtaposition.
For bilinear forms of any signature
, an orthogonal basis
{e1,...,en} can be found for V such that each ei2 is either −1, 0 or +1. The number of each case is dictated by the signature.
When Q is nondegenerate there are no 0's in the signature, and so an orthogonal basis of V exists with p elements squaring to 1 and q elements squaring to −1, with . We denote this algebra
. For example, 
models 3D Euclidean space
,
relativistic spacetime
and
a 3D Conformal Geometric algebra.
given by . This is the inner product for V discussed below. With respect to this bilinear form, a basis
for V can be found such that
for all (othogonality) and
The set of all possible products of these n symbols with indices in increasing order, including 1 as the empty product, forms a basis for the geometric algebra. As an illustration, the following is a basis for the geometric algebra
:
A basis formed this way is called a standard basis for the geometric algebra, and any other orthogonal basis for V fitting the above description will produce another standard basis. Each standard basis consists of 2n elements. The geometric product between elements of the algebra is completely described by the rules:
These first four rules give the geometric product of any two elements in the standard basis as another up to a sign or zero. A few example computations follow:
The geometric product of any two elements in the algebra can be computed with these rules, including the last. Specifically, if the standard basis elements with S being an index set, then
Standard bases may be used to define grades (not to be confused with a grading
over the geometric product) of some elements in the geometric algebra. Normal vectors in the span of
are called 1-vectors. Scalars are called 0-vectors. Elements in the span of 
are called 2-vectors, and elements in the span of 
are called 3-vectors and so on until the last grade of n-vectors. Many of the elements of the algebra are not graded by this scheme since they are sums of elements of differing grade. Such elements are said to be of mixed grade.
Generic elements of the geometric algebra are usually called multivectors with the term vector usually reserved for 1-vectors. The grading of multivectors is independent of the orthogonal basis chosen originally.
A multivector
may be decomposed with the grade projection operator 
which outputs the grade r portion of A. As a result:
As an example, the geometric product of two vectors
since 
and 
and 
for i other than 0 and 2.
If for some vector a, then a−1 exists and is equal to . For a positive-definite or negative-definite quadratic form, all nonzero vectors have multiplicative inverses. Not all the elements of the algebra are invertible. For example, if u is a unit vector in V (i.e. a vector such that , the elements have no inverse since they are zero divisor
s: .
Vectors will be represented by lower case letters (e.g. ), and multivectors by upper case letters (e.g. ). Scalars will be represented by Greek characters.
and using the geometric product to form the blade . There are multiple blades representing W; all those representing W are scalar multiples of D. These blades can be separated into two sets: positive multiples of D and negative multiples of D. The positive multiples of D are said to have the same orientation as D, and the negative multiples the opposite orientation.
Blades are important since geometric operations such as projections, rotations and reflections are implemented by using the geometric product to multiply vectors and blades.
Suppose the geometric algebra
with the familiar positive definite inner product on Rn is formed. Given a plane (2-dimensional subspace) of Rn, one can find an orthonormal basis {b1,b2} spanning the plane, and thus find a pseudoscalar representing this plane. The geometric product of any two vectors in the span of b1 and b2 lies in 
, that is, it is the sum of a 0-vector and a 2-vector.
By the properties of the geometric product, . The resemblance to the imaginary unit
is not accidental: the subspace
is R-algebra isomorphic to the complex number
s. In this way, a copy of the complex numbers is embedded in the geometric algebra for each 2-dimensional subspace of V.
It is sometimes possible to identify the presence of an imaginary unit in a physical equation. Such units arise from one of the many quantities in the real algebra that square to −1, and these have geometric significance because of the properties of the algebra and the interaction of its various subspaces.
In
, an exceptional case occurs. Given a standard basis built from orthonormal ei's from V, the set of all 2-vectors is generated by
.
Labelling these i, j and k (momentarily deviating from our uppercase convention), the subspace generated by 0-vectors and 2-vectors is exactly
. This set is seen to be a subalgebra, and furthermore is R-algebra isomorphic to the quaternion
s, another important algebraic system.
The inner product on vectors can also be generalised, but in more than one non-equivalent way. The paper gives a full treatment of several different inner products developed for geometric algebras and their interrelationships. Among these several different generalizations are:
makes an argument for the use of contractions in preference to Hestenes's inner product (below); they are algebraically more regular and have cleaner geometric interpretations. A number of identities relating these products are valid without restriction of their inputs. Benefits of using the left contraction as an extension of the inner product on vectors are that the identity
is extended to 
for a vector a and any multivector B, and that the projection
operation
is extended to 
for any blades A and B.
The inner product generalization introduced by D. Hestenes ignores the scalar component of both inputs, and must be used care with respect to the grades in each input:
may be directly compared
to vector algebra.
The even subalgebra
of
is isomorphic to the complex number
s, as may be seen by writing a vector in terms of its components in an orthonormal basis and left multiplying by the basis vector , yielding
where we identify since
Similarly, the even subalgebra of
with basis is isomorphic to the quaternion
s as may be seen by identifing , and .
Every associative algebra
has a matrix representation; the Pauli matrices
are a representation of
and the Dirac matrices are a representation of 
, showing the equivalence with matrix representations used by physicists.
then we denote the reverse as
.
As an example, assume that
we get
.
Scaling so that then
so
† leaves the length of 
unchanged. We can also show that
so the transformation preserves both length and angle. It therefore can be identified as a rotation or rotoreflection; is called a rotor
if it is a proper rotation (as it is if it can be expressed as a product of an even number of vectors) and is an instance of what is known in GA as a versor (presumably for historical reasons).
There is a general method for rotating a vector involving the formation of a multivector of the form
that produces an anticlockwise rotation 
in the plane defined by a bivector 
.
Rotors are a generalization of quaternions to n-D spaces.
For more about reflections, rotations and "sandwiching" products like see Plane of rotation
.
Essentially, the vector derivative is defined so that the GA version of Green's theorem
is true,
and then one can write
as a geometric product, effectively generalizing Stokes theorem (including the differential forms version of it).
In
when A is a curve with endpoints 
and 
, then
reduces to
or the fundamental theorem of integral calculus.
Also developed are the concept of vector manifold and geometric integration theory (which generalizes Cartan's differential forms).
This again extends the language of GA, the conformal model of
is embedded in the CGA 
via the identification of Euclidean points with 
vectors in the 
null cone, adding a point at infinity and normalizing all points to the hyperplane
. Allows all of conformal algebra to be done by combinations of rotations and reflections and the language is covariant, permitting the extension of incidence relations of projective geometry to circles and spheres.
Specifically, we add
such that 
and 
such that 
to the orthonormal basis of 
allowing the creation of
representing an ideal point (point at infinity)(see Compactification
)
representing the origin where
and 
where 
is a unit pseudoscalar
representing the Minkowski plane
.
This procedure has some similarities to the procedure for working with homogeneous coordinates
in projective geometry and in this case allows the modeling of Euclidean transformations as Orthogonal transformations.
A fast changing and fluid area of GA, CGA is also being investigated for applications to
relativistic physics.
The following is a list of freely available software that does not require ownership of commercial software or purchase of any commercial products for this purpose:
The link provides a manual, introduction to GA and sample material as well as the software.
Software allowing script creation and including sample visualizations, manual and GA introduction.
For programmers,this is a code generator with support for C,C++,C# and Java.
is a 
-blade then a vector 
has a projection or parallel component 
onto 
,
and a rejection or perpendicular component
So for vectors
and 
in 2D we have
or 
and we have that
is the product of the "altitude" and the "base" of the 
-parallelogram, that is, its area.
We may define the line parametrically by
where p and t are position vectors for points T and P and v is the direction vector for the line.
Then
and 
so
and
.
(APS), and the geometric algebra of Minkowski 3+1 spacetime, Cl3,1, called spacetime algebra
(STA).
In APS, points of (3+1)-dimensional space-time are represented by paravector
s: a 3-dimensional vector (space) plus a 1-dimensional scalar (time), while in STA points of space-time are represented simply by vectors.
In spacetime algebra the electromagnetic field tensor has a bivector representation
where the imaginary unit is the volume element, and where Maxwell's equations
simplify to one equation:
Boosts in this Lorenzian metric space have the same expression
as rotation in Euclidean space, where 
is the bivector generated by the time and the space directions involved, whereas in the Euclidean case it is the bivector generated by the two space directions, strengthening the "analogy" to almost identity.
and angular momentum
make use of the Cross product
.
The cross product can be viewed in terms of the outer product allowing a more natural geometric interpretation of the cross product as a bivector using the dual
relationship
For example,torque is generally defined as the magnitude of the perpendicular force component times distance, or work per unit angle.
Suppose a circular path in an arbitrary plane containing orthonormal vectors
and
is parameterized by angle.
By designating the unit bivector of this plane as the imaginary number
this path vector can be conveniently written in complex exponential form
and the derivative with respect to angle is
So the torque, the rate of change of work W, due to a forceF, is
Unlike the cross product description of torque,
, the geometric-algebra description does not introduce a vector in the normal direction; a vector that does not exist in two and that is not unique in greater than three dimensions. The unit bivector describes the plane and the orientation of the rotation, and the sense of the rotation is relative to the angle between the vectors 
and 
.
's Elements
in the 3rd century B.C. (see Greek geometric algebra),
GA in the sense used in this article was not developed until 1844, when it was used in a systematic way to describe the geometrical properties and transformations of a space. In that year, Hermann Grassmann
introduced the idea of a geometrical algebra in full generality as a certain calculus (analogous to the propositional calculus
) which encoded all of the geometrical information of a space. Grassmann's algebraic system could be applied to a number of different kinds of spaces: the chief among them being Euclidean space
, affine space
, and projective space
. Following Grassmann, in 1878 William Kingdon Clifford
examined Grassmann's algebraic system alongside the quaternions of William Rowan Hamilton
in . From his point of view, the quaternions described certain transformations (which he called rotors), whereas Grassmann's algebra described certain properties (or Strecken such as length, area, and volume). His contribution was to define a new product — the geometric product — on an existing Grassmann algebra, which realized the quaternions as living within that algebra. Subsequently Rudolf Lipschitz
in 1886 generalized Clifford's interpretation of the quaternions and applied them to the geometry of rotations in n dimensions. Later these developments would lead other 20th-century mathematicians to formalize and explore the properties of the Clifford algebra.
Nevertheless, another revolutionary development of the 19th-century would completely overshadow the geometric algebras: that of vector analysis, developed independently by Josiah Willard Gibbs
and Oliver Heaviside
. Vector analysis was motivated by James Clerk Maxwell
's studies of electromagnetism
, and specifically the need to express and manipulate conveniently certain differential equation
s. Vector analysis had a certain intuitive appeal compared to the rigors of the new algebras. Physicists and mathematicians alike readily adopted it as their geometrical toolkit of choice, particularly following the influential 1901 textbook Vector Analysis by Edwin Bidwell Wilson
, following lectures of Gibbs.
In more detail, there have been three approaches to geometric algebra: quaternion
ic analysis, initiated by Hamilton in 1843 and geometrized as rotors by Clifford in 1878; geometric algebra, initiated by Grassmann in 1844; and vector analysis, developed out of quaternionic analysis in the late 19th century by Gibbs and Heaviside. The legacy of quaternionic analysis in vector analysis can be seen in the use of
to indicate the basis vectors of 
it is being thought of as the purely imaginary quaternions. From the perspective of geometric algebra, quaternions can be identified as Cℓ+3,0(R), the even part of the Clifford algebra on Euclidean 3-space, which unifies the three approaches.
ists such as Hermann Weyl
and Claude Chevalley
. The geometrical approach to geometric algebras has seen a number of 20th-century revivals. In mathematics, Emil Artin
's Geometric Algebra discusses the algebra associated with each of a number of geometries, including affine geometry
, projective geometry
, symplectic geometry, and orthogonal geometry. In physics, geometric algebras have been revived as a "new" way to do classical mechanics and electromagnetism, together with more advanced topics such as quantum mechanics and gauge theory. David Hestenes
reinterpreted the Pauli and Dirac matrices as vectors in ordinary space and spacetime, respectively, and has been a primary contemporary advocate for the use of geometric algebra.
In computer graphics
, geometric algebras have been revived in order to represent efficiently rotations (and other transformations) on computer hardware.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. GA now finds application in all of physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, in graphics
Graphics
Graphics are visual presentations on some surface, such as a wall, canvas, computer screen, paper, or stone to brand, inform, illustrate, or entertain. Examples are photographs, drawings, Line Art, graphs, diagrams, typography, numbers, symbols, geometric designs, maps, engineering drawings,or...
and in robotics
Robotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
. GA is Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
over the field of real numbers, where the naturally embedded Grassmann algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
plays a part. Spacetime algebra
Spacetime algebra
In mathematical physics, spacetime algebra is a name for the Clifford algebra Cℓ1,3,or Geometric algebra G4 = G which can be particularly closely associated with the geometry of special relativity and relativistic spacetime....
and Conformal Geometric algebra are specific examples of GA.
A feature of GA is its geometric interpretation due to the natural correspondence between geometric entities and the elements of the algebra. GA allows direct manipulation of subspaces and is a coordinate-free formalism. Proponents argue that it provides compact and intuitive descriptions in many areas including classical
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, electromagnetic theory and relativity
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
among others. In many cases, the "proliferation of manifolds" that occurs during the standard curriculum of differential geometry can be reduced by working with real-only algebras.
Definition and Notation
This section begins with a brief, formal description, but then it will demonstrate easy to understand properties of the geometric algebra in a concrete way.Given a finite dimensional real quadratic space with quadratic form , the geometric algebra for this quadratic space is the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
Cℓ(V,Q).
The algebra product is called the geometric product, and it is just the Clifford product. It is standard to denote the geometric product by juxtaposition.
For bilinear forms of any signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
, an orthogonal basis
Orthogonal basis
In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...
{e1,...,en} can be found for V such that each ei2 is either −1, 0 or +1. The number of each case is dictated by the signature.
When Q is nondegenerate there are no 0's in the signature, and so an orthogonal basis of V exists with p elements squaring to 1 and q elements squaring to −1, with . We denote this algebra
. For example, models 3D Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
,
relativistic spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
and
a 3D Conformal Geometric algebra.Standard bases and grading
The geometric product creates a symmetric bilinear formSymmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
given by . This is the inner product for V discussed below. With respect to this bilinear form, a basis
for V can be found such that for all (othogonality) andThe set of all possible products of these n symbols with indices in increasing order, including 1 as the empty product, forms a basis for the geometric algebra. As an illustration, the following is a basis for the geometric algebra
:A basis formed this way is called a standard basis for the geometric algebra, and any other orthogonal basis for V fitting the above description will produce another standard basis. Each standard basis consists of 2n elements. The geometric product between elements of the algebra is completely described by the rules:
for (orthogonal vectors anticommute)
(scalars commute)
(associativity of the geometric product)
and 
(distributivity of the geometric product over addition).
These first four rules give the geometric product of any two elements in the standard basis as another up to a sign or zero. A few example computations follow:
The geometric product of any two elements in the algebra can be computed with these rules, including the last. Specifically, if the standard basis elements with S being an index set, then
Standard bases may be used to define grades (not to be confused with a grading
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
over the geometric product) of some elements in the geometric algebra. Normal vectors in the span of
are called 1-vectors. Scalars are called 0-vectors. Elements in the span of are called 2-vectors, and elements in the span of are called 3-vectors and so on until the last grade of n-vectors. Many of the elements of the algebra are not graded by this scheme since they are sums of elements of differing grade. Such elements are said to be of mixed grade.Generic elements of the geometric algebra are usually called multivectors with the term vector usually reserved for 1-vectors. The grading of multivectors is independent of the orthogonal basis chosen originally.
A multivector
may be decomposed with the grade projection operator which outputs the grade r portion of A. As a result:
As an example, the geometric product of two vectors
since and and for i other than 0 and 2.Inner and outer products
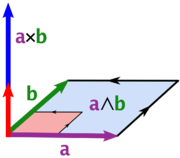
There are two other important operations on in the geometric algebra besides the geometric product. Let a and b be elements of V:- The inner product on V is the symmetric bilinear formSymmetric bilinear formA symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
arising as the symmetric part of geometric multiplication (and equivalently the bilinear form arising from the quadratic form Q), and is denoted by
. It is related to the geometric product and quadratic form by these equations:
- The inner product of two vectors is always a 0-vector of the algebra.
- The outer product on V, denoted with ∧, arises as the antisymmetric part of the geometric product:
- The outer product on V, denoted with ∧, arises as the antisymmetric part of the geometric product:
- The outer product of two vectors is always a 2-vector of the algebra.
- The inner and outer products are united into the geometric product since
,
- The inner and outer products are united into the geometric product since
- Thus the geometric product of two vectors is in general of mixed grade.
If for some vector a, then a−1 exists and is equal to . For a positive-definite or negative-definite quadratic form, all nonzero vectors have multiplicative inverses. Not all the elements of the algebra are invertible. For example, if u is a unit vector in V (i.e. a vector such that , the elements have no inverse since they are zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s: .
Vectors will be represented by lower case letters (e.g. ), and multivectors by upper case letters (e.g. ). Scalars will be represented by Greek characters.
Representation of subspaces
Geometric algebra represents subspaces of V as multivectors, and so they coexist in the same algebra with vectors from V. A k dimensional subspace W of V is represented by taking an orthogonal basis and using the geometric product to form the blade . There are multiple blades representing W; all those representing W are scalar multiples of D. These blades can be separated into two sets: positive multiples of D and negative multiples of D. The positive multiples of D are said to have the same orientation as D, and the negative multiples the opposite orientation.Blades are important since geometric operations such as projections, rotations and reflections are implemented by using the geometric product to multiply vectors and blades.
Pseudoscalars
Pseudoscalars are blades that play important roles in GA. A pseudoscalar for a subspace W of V is a blade that is the product of the members of an orthonormal basis for W. It can be shown that if and are both pseudoscalars for W, then .Suppose the geometric algebra
with the familiar positive definite inner product on Rn is formed. Given a plane (2-dimensional subspace) of Rn, one can find an orthonormal basis {b1,b2} spanning the plane, and thus find a pseudoscalar representing this plane. The geometric product of any two vectors in the span of b1 and b2 lies in , that is, it is the sum of a 0-vector and a 2-vector.By the properties of the geometric product, . The resemblance to the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
is not accidental: the subspace
is R-algebra isomorphic to the complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. In this way, a copy of the complex numbers is embedded in the geometric algebra for each 2-dimensional subspace of V.
It is sometimes possible to identify the presence of an imaginary unit in a physical equation. Such units arise from one of the many quantities in the real algebra that square to −1, and these have geometric significance because of the properties of the algebra and the interaction of its various subspaces.
In
, an exceptional case occurs. Given a standard basis built from orthonormal ei's from V, the set of all 2-vectors is generated by.Labelling these i, j and k (momentarily deviating from our uppercase convention), the subspace generated by 0-vectors and 2-vectors is exactly
. This set is seen to be a subalgebra, and furthermore is R-algebra isomorphic to the quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, another important algebraic system.
Extensions of the inner and outer products
It is common practice to extend the outer product on vectors to the entire algebra. This may be done through the use of the grade projection operator:-
(the outer product)
The inner product on vectors can also be generalised, but in more than one non-equivalent way. The paper gives a full treatment of several different inner products developed for geometric algebras and their interrelationships. Among these several different generalizations are:
-
(the left contraction) -
(the right contraction) -
(the scalar product) -
(the "(fat) dot" product)
makes an argument for the use of contractions in preference to Hestenes's inner product (below); they are algebraically more regular and have cleaner geometric interpretations. A number of identities relating these products are valid without restriction of their inputs. Benefits of using the left contraction as an extension of the inner product on vectors are that the identity
is extended to for a vector a and any multivector B, and that the projectionProjection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
operation
is extended to for any blades A and B.The inner product generalization introduced by D. Hestenes ignores the scalar component of both inputs, and must be used care with respect to the grades in each input:
-
(Hestenes's inner product)
Relationship with other formalisms
may be directly comparedComparison of vector algebra and geometric algebra
Vector algebra and geometric algebra are alternative approaches to providing additional algebraic structures on vector spaces, with geometric interpretations, particularly vector fields in multivariable calculus and applications in mathematical physics....
to vector algebra.
The even subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of
is isomorphic to the complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, as may be seen by writing a vector in terms of its components in an orthonormal basis and left multiplying by the basis vector , yielding
where we identify since
Similarly, the even subalgebra of
with basis is isomorphic to the quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s as may be seen by identifing , and .
Every associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
has a matrix representation; the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
are a representation of
and the Dirac matrices are a representation of , showing the equivalence with matrix representations used by physicists.Rotations
If we have a product of vectors then we denote the reverse as.As an example, assume that
we get.Scaling so that then
so
† leaves the length of unchanged. We can also show thatso the transformation preserves both length and angle. It therefore can be identified as a rotation or rotoreflection; is called a rotor
Rotor (mathematics)
A rotor is an n-blade object in geometric algebra, which rotates another n-blade object about a fixed or translated point. They are normally motivated by considering an even number of reflections, which generate rotations...
if it is a proper rotation (as it is if it can be expressed as a product of an even number of vectors) and is an instance of what is known in GA as a versor (presumably for historical reasons).
There is a general method for rotating a vector involving the formation of a multivector of the form
that produces an anticlockwise rotation in the plane defined by a bivector .Rotors are a generalization of quaternions to n-D spaces.
For more about reflections, rotations and "sandwiching" products like see Plane of rotation
Plane of rotation
In geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
.
Geometric Calculus
Geometric Calculus extends the formalism to include differentiation and integration including differential geometry and differential forms.Essentially, the vector derivative is defined so that the GA version of Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
is true,
and then one can write
as a geometric product, effectively generalizing Stokes theorem (including the differential forms version of it).
In
when A is a curve with endpoints and , thenreduces to
or the fundamental theorem of integral calculus.
Also developed are the concept of vector manifold and geometric integration theory (which generalizes Cartan's differential forms).
Conformal Geometric Algebra (CGA)
A compact description of the current state of the art is provided by Bayro-Corrochano and Scheuermann (2010), which also includes further references, in particular to Dorst et al (2007). Another useful reference is Li (2008).This again extends the language of GA, the conformal model of
is embedded in the CGA via the identification of Euclidean points with vectors in the null cone, adding a point at infinity and normalizing all points to the hyperplaneHyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
. Allows all of conformal algebra to be done by combinations of rotations and reflections and the language is covariant, permitting the extension of incidence relations of projective geometry to circles and spheres.Specifically, we add
such that and such that to the orthonormal basis of allowing the creation of representing an ideal point (point at infinity)(see CompactificationCompactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
)
representing the origin where and where is a unit pseudoscalarPseudoscalar
In physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
representing the Minkowski plane
Minkowski plane
In mathematics, the Minkowski plane is a two-dimensional affine space provided with a metric that is invariant under translations.Often one identifies the underlying affine space with the plane R2....
.
This procedure has some similarities to the procedure for working with homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
in projective geometry and in this case allows the modeling of Euclidean transformations as Orthogonal transformations.
A fast changing and fluid area of GA, CGA is also being investigated for applications to
relativistic physics.
Software
GA is a very application oriented subject. There is a reasonably steep initial learning curve associated with it, but this can be eased somewhat by the use of applicable software.The following is a list of freely available software that does not require ownership of commercial software or purchase of any commercial products for this purpose:
- GA Viewer Fontijne, Dorst, Bouma & Mann
The link provides a manual, introduction to GA and sample material as well as the software.
- CLUViz Perwass
Software allowing script creation and including sample visualizations, manual and GA introduction.
- Gaigen Fontijne
For programmers,this is a code generator with support for C,C++,C# and Java.
Area of parallelogram spanned by two vectors
If is a -blade then a vector has a projection or parallel component onto ,and a rejection or perpendicular component
So for vectors
and in 2D we have or and we have that
is the product of the "altitude" and the "base" of the -parallelogram, that is, its area.Intersection of a line and a plane
Consider a line L defined by points T and P (which we seek) and a plane defined by a bivector B containing points P and Q.We may define the line parametrically by
where p and t are position vectors for points T and P and v is the direction vector for the line.Then
and so
and
.Electrodynamics and special relativity
In physics, the main applications are the geometric algebra of Euclidean 3-space, Cl3, called the Algebra of physical spaceAlgebra of physical space
In physics, the algebra of physical space is the use of the Clifford or geometric algebra Cℓ3 of the three-dimensional Euclidean space as a model for -dimensional space-time, representing a point in space-time via a paravector .The Clifford algebra Cℓ3 has a faithful representation, generated by...
(APS), and the geometric algebra of Minkowski 3+1 spacetime, Cl3,1, called spacetime algebra
Spacetime algebra
In mathematical physics, spacetime algebra is a name for the Clifford algebra Cℓ1,3,or Geometric algebra G4 = G which can be particularly closely associated with the geometry of special relativity and relativistic spacetime....
(STA).
In APS, points of (3+1)-dimensional space-time are represented by paravector
Paravector
The name paravector is used for the sum of a scalar and a vector in any Clifford algebra This name was given by J. G...
s: a 3-dimensional vector (space) plus a 1-dimensional scalar (time), while in STA points of space-time are represented simply by vectors.
In spacetime algebra the electromagnetic field tensor has a bivector representation
where the imaginary unit is the volume element, and where Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
simplify to one equation:
Boosts in this Lorenzian metric space have the same expression
as rotation in Euclidean space, where is the bivector generated by the time and the space directions involved, whereas in the Euclidean case it is the bivector generated by the two space directions, strengthening the "analogy" to almost identity.Rotational Systems
The mathematical description of rotational forces such as TorqueTorque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
make use of the Cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
.
Hodge dual
In mathematics, the Hodge star operator or Hodge dual is a significant linear map introduced in general by W. V. D. Hodge. It is defined on the exterior algebra of a finite-dimensional oriented inner product space.-Dimensions and algebra:...
relationship
For example,torque is generally defined as the magnitude of the perpendicular force component times distance, or work per unit angle.
Suppose a circular path in an arbitrary plane containing orthonormal vectors
and is parameterized by angle.By designating the unit bivector of this plane as the imaginary number
this path vector can be conveniently written in complex exponential form
and the derivative with respect to angle is
So the torque, the rate of change of work W, due to a forceF, is
Unlike the cross product description of torque,
, the geometric-algebra description does not introduce a vector in the normal direction; a vector that does not exist in two and that is not unique in greater than three dimensions. The unit bivector describes the plane and the orientation of the rotation, and the sense of the rotation is relative to the angle between the vectors and .History
Although the connection of geometry with algebra dates as far back at least to EuclidEuclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
in the 3rd century B.C. (see Greek geometric algebra),
GA in the sense used in this article was not developed until 1844, when it was used in a systematic way to describe the geometrical properties and transformations of a space. In that year, Hermann Grassmann
Hermann Grassmann
Hermann Günther Grassmann was a German polymath, renowned in his day as a linguist and now also admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher...
introduced the idea of a geometrical algebra in full generality as a certain calculus (analogous to the propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
) which encoded all of the geometrical information of a space. Grassmann's algebraic system could be applied to a number of different kinds of spaces: the chief among them being Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, and projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. Following Grassmann, in 1878 William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
examined Grassmann's algebraic system alongside the quaternions of William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in . From his point of view, the quaternions described certain transformations (which he called rotors), whereas Grassmann's algebra described certain properties (or Strecken such as length, area, and volume). His contribution was to define a new product — the geometric product — on an existing Grassmann algebra, which realized the quaternions as living within that algebra. Subsequently Rudolf Lipschitz
Rudolf Lipschitz
Rudolf Otto Sigismund Lipschitz was a German mathematician and professor at the University of Bonn from 1864. Peter Gustav Dirichlet was his teacher. He supervised the early work of Felix Klein....
in 1886 generalized Clifford's interpretation of the quaternions and applied them to the geometry of rotations in n dimensions. Later these developments would lead other 20th-century mathematicians to formalize and explore the properties of the Clifford algebra.
Nevertheless, another revolutionary development of the 19th-century would completely overshadow the geometric algebras: that of vector analysis, developed independently by Josiah Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
and Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
. Vector analysis was motivated by James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
's studies of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, and specifically the need to express and manipulate conveniently certain differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. Vector analysis had a certain intuitive appeal compared to the rigors of the new algebras. Physicists and mathematicians alike readily adopted it as their geometrical toolkit of choice, particularly following the influential 1901 textbook Vector Analysis by Edwin Bidwell Wilson
Edwin Bidwell Wilson
Edwin Bidwell Wilson was an American mathematician and polymath. He was the sole protégé of Yale's physicist Josiah Willard Gibbs and was mentor to MIT economist Paul Samuelson. He received his AB from Harvard College in 1899 and his PhD from Yale University in 1901, working under Gibbs.E.B...
, following lectures of Gibbs.
In more detail, there have been three approaches to geometric algebra: quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
ic analysis, initiated by Hamilton in 1843 and geometrized as rotors by Clifford in 1878; geometric algebra, initiated by Grassmann in 1844; and vector analysis, developed out of quaternionic analysis in the late 19th century by Gibbs and Heaviside. The legacy of quaternionic analysis in vector analysis can be seen in the use of
to indicate the basis vectors of it is being thought of as the purely imaginary quaternions. From the perspective of geometric algebra, quaternions can be identified as Cℓ+3,0(R), the even part of the Clifford algebra on Euclidean 3-space, which unifies the three approaches.20th century and Present
Progress on the study of Clifford algebras quietly advanced through the twentieth century, although largely due to the work of abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
ists such as Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
and Claude Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
. The geometrical approach to geometric algebras has seen a number of 20th-century revivals. In mathematics, Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
's Geometric Algebra discusses the algebra associated with each of a number of geometries, including affine geometry
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
, projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, symplectic geometry, and orthogonal geometry. In physics, geometric algebras have been revived as a "new" way to do classical mechanics and electromagnetism, together with more advanced topics such as quantum mechanics and gauge theory. David Hestenes
David Hestenes
David Orlin Hestenes, Ph.D. is a physicist. For more than 30 years, he was employed in the Department of Physics and Astronomy of Arizona State University , where he retired with the rank of Research Professor and is now emeritus....
reinterpreted the Pauli and Dirac matrices as vectors in ordinary space and spacetime, respectively, and has been a primary contemporary advocate for the use of geometric algebra.
In computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, geometric algebras have been revived in order to represent efficiently rotations (and other transformations) on computer hardware.
See also
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
- Algebra of physical spaceAlgebra of physical spaceIn physics, the algebra of physical space is the use of the Clifford or geometric algebra Cℓ3 of the three-dimensional Euclidean space as a model for -dimensional space-time, representing a point in space-time via a paravector .The Clifford algebra Cℓ3 has a faithful representation, generated by...
- Spacetime algebraSpacetime algebraIn mathematical physics, spacetime algebra is a name for the Clifford algebra Cℓ1,3,or Geometric algebra G4 = G which can be particularly closely associated with the geometry of special relativity and relativistic spacetime....
- SpinorSpinorIn mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
- QuaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
Further reading
- Baylis, W. E., ed., 1996. Clifford (Geometric) Algebra with Applications to Physics, Mathematics, and Engineering. Boston: Birkhäuser.
- Baylis, W. E., 2002. Electrodynamics: A Modern Geometric Approach, 2nd ed. Birkhäuser. ISBN 0-8176-4025-8
- Nicolas BourbakiNicolas BourbakiNicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
, 1980. Eléments de Mathématique. Algèbre. Chpt. 9, "Algèbres de Clifford". Paris: Hermann. - Hestenes, D.David HestenesDavid Orlin Hestenes, Ph.D. is a physicist. For more than 30 years, he was employed in the Department of Physics and Astronomy of Arizona State University , where he retired with the rank of Research Professor and is now emeritus....
, 1999. New Foundations for Classical Mechanics, 2nd ed. Springer Verlag ISBN 0-7923-5302-1 - Lasenby, J., Lasenby, A. N., and Doran, C. J. L., 2000, "A Unified Mathematical Language for Physics and Engineering in the 21st Century," Philosophical Transactions of the Royal Society of London A 358: 1-18.
External links
- Imaginary Numbers are not Real - the Geometric Algebra of Spacetime. Introduction (Cambridge GA group).
- Physical Applications of Geometric Algebra. Final-year undergraduate course by Chris Doran and Anthony Lasenby (Cambridge GA group; see also 1999 version).
- Maths for (Games) Programmers: 5 - Multivector methods. Comprehensive introduction and reference for programmers, from Ian BellIan Bell (programmer)Ian Colin Graham Bell is a game programmer, game designer and game producer. He is most famous for co-authoring the computer game Elite .He attended the independent St Albans School...
. - Clifford algebra, geometric algebra, and applications Douglas Lundholm, Lars Svensson Lecture notes for a course on the theory of Clifford algebras, with special emphasis on their wide range of applications in mathematics and physics.
- IMPA SUmmer School 2010 Fernandes Oliveira Intro and Slides.
- University of Fukui E.S.M. Hitzer and Japan GA publications.
- Google Group for GA
Research groups
- Geometric Calculus International. Links to Research groups, Software, and Conferences, worldwide.
- Cambridge Geometric Algebra group. Full-text online publications, and other material.
- University of Amsterdam group
- Geometric Calculus research & development (Arizona State University).
- GA-Net blog and newsletter archive. Geometric Algebra/Clifford Algebra development news.