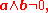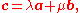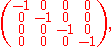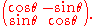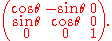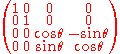Plane of rotation
Encyclopedia
In geometry
, a plane of rotation is an abstract object used to describe or visualise rotation
s in space. In three dimensions it is an alternative to the axis of rotation
, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.
Mathematically such planes can be described in a number of ways. They can be described in terms of planes and angle
s of rotation. They can be associated with bivector
s from geometric algebra
. They are related to the eigenvalues and eigenvectors of a rotation matrix. And in particular dimension
s they are related to other algebraic and geometric properties, which can then be generalised to other dimensions.
Planes of rotation are not used much in two and three dimensions, as in two dimensions there is only one plane so identifying the plane of rotation is trivial and rarely done, while in three dimensions the axis of rotation serves the same purpose and is the more established approach. The main use for them is in describing more complex rotations in higher dimensions, where they can be used to break down the rotations into simpler parts. This can be done using geometric algebra
, with the planes of rotations associated with simple bivectors in the algebra.
, that is they contain the zero vector. Such a plane in n-dimensional space is a 2-dimensional linear subspace
of the space. It is completely specified by any two non-zero and non-parallel vectors that lie in the plane, that is by any two vectors a and b, such that
where ∧ is the exterior product from exterior algebra
or geometric algebra
(in three dimensions the cross product
can be used). More precisely the quantity a ∧ b is the bivector associated with the plane specifed by a and b, and has magnitude |a| |b| sin φ, where φ is the angle between the vectors; hence the requirement that the vectors be non-zero and non-parallel.
If the bivector a ∧ b is written B then the condition that a point lies on the plane associated with B is simply
This is true in all dimensions, and can be taken as the definition on the plane. In particular, from the properties of the exterior product it is satisfied by both a and b, and so by any vector of the form
with λ and μ real numbers. As λ and μ range over all real numbers c ranges over the whole plane, so this can be taken as another definition of the plane.
is a plane that is mapped to itself by the rotation. The plane is not fixed, but all vectors in the plane are mapped to other vectors in the same plane by the rotation. This transformation of the plane to itself is always a rotation about the origin, through an angle which is the angle of rotation
for the plane.
Every rotation except for the identity
rotation (with matrix the identity matrix
) has at least one plane of rotation, and up to
planes of rotation, where n is the dimension. The maximum number of planes up to eight dimensions is shown in this table:
When a rotation has multiple planes of rotation they are always orthogonal to each other, with only the origin in common. This is a stronger condition than to say the planes are at right angle
s; it instead means that the planes have no nonzero vectors in common, and that every vector in one plane is orthogonal to every vector in the other plane. This can only happen in four or more dimensions. In two dimensions there is only one plane, while in three dimensions all planes have at least one nonzero vector in common, along their line of intersection.
In more than three dimensions planes of rotation are not always unique. For example the negative of the identity matrix
in four dimensions (the central inversion),
describes a rotation in four dimensions in which every plane through the origin is a plane of rotation through an angle π, so any pair of orthogonal planes generates the rotation. But for a general rotation it is at least theoretically possible to identify a unique set of orthogonal planes, in each of which points are rotated through an angle, so the set of planes and angles fully characterise the rotation.
there is only one plane of rotation, the plane of the space itself. In a Cartesian coordinate system
it is the Cartesian plane, in complex numbers it is the complex plane
. Any rotation therefore is of the whole plane, i.e. of the space, keeping only the origin
fixed. It is specified completely by the signed angle of rotation, in the range for example −π to π. So if the angle is θ the rotation in the complex plane is given by Euler's formula
:
while the rotation in a Cartesian plane is given by the 2×2 rotation matrix:
there are an infinite number of planes of rotation, only one of which is involved in any given rotation. That is for a general rotation there is precisely one plane which is associated with it or which the rotation takes place in. The only exception is the trivial rotation, corresponding to the identity matrix, in which no rotation takes place.
In any rotation in three dimensions there is always a fixed axis, the axis of rotation. The rotation can described by giving this axis, with the angle through which the rotation turns about it; this is the axis angle
representation of a rotation. The plane of rotation is the plane orthogonal to this axis, so the axis is a surface normal
of the plane. The rotation then rotates this plane through the same angle as it rotates around the axis, that is everything in the plane rotates by the same angle about the origin.
One example is shown in the diagram, where the rotation takes place about the z-axis. The plane of rotation is the xy-plane, so everything in that plane it kept in the plane by the rotation. This could be described by a matrix like the following, with the rotation being through an angle θ (about the axis or in the plane):
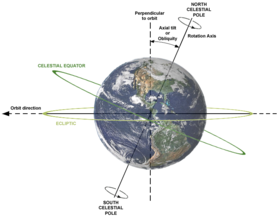Another example is the Earth's rotation. The axis of rotation is the line joining the North Pole
and South Pole
and the plane of rotation is the plane through the equator
between the Northern
and Southern
Hemispheres. Other examples include mechanical devices like a gyroscope
or flywheel
which store rotational energy
in mass usually along the plane of rotation.
In any three dimensional rotation the plane of rotation is uniquely defined. Together with the angle of rotation it fully describes the rotation. Or in a continuously rotating object the rotational properties such as the rate of rotation can be described in terms of the plane of rotation. It is perpendicular to, and so is defined by and defines, an axis of rotation, so any description of a rotation in terms of a plane of rotation can be described in terms of an axis of rotation, and vice-versa. But unlike the axis of rotation the plane generalises into other, in particular higher, dimensions.
For example the following matrix fixes the xy-plane: points in that plane and only in that plane are unchanged. The plane of rotation is the zw-plane, points in this plane are rotated through an angle θ. A general point rotates only in the zw-plane, that is it rotates around the xy-plane by changing only its z and w coordinates.
In two and three dimensions all rotations are simple, in that they have only one plane of rotation. Only in four and more dimensions are there rotations that are not simple simple rotations. In particular in four dimensions there are also double and isoclinic rotations.
A double rotation has two angles of rotation, one for each plane of rotation. The rotation is specified by giving the two planes and two non-zero angles, α and β (if either angle is zero the rotation is simple). Points in the first plane rotate through α, while points in the second plane rotate through β. All other points rotate through an angle between α and β, so in a sense they together determine the amount of rotation. For a general double rotation the planes of rotation and angles are unique, and given a general rotation they can be calculated. For example a rotation of α in the xy-plane and β in the zw-plane is given by the matrix
so the complexity quickly increases with more than four dimensions and categorising rotations as above becomes too complex to be practical, but some observations can be made.
Simple rotations can be identified in all dimensions, as rotations with just one plane of rotation. A simple rotation in n dimensions takes place about (that is at a fixed distance from) an -dimensional subspace orthogonal to the plane of rotation.
A general rotation is not simple, and has the maximum number of planes of rotation as given above. In the general case the angles of rotations in these planes are distinct and the planes are uniquely defined. If any of the angles are the same then the planes are not unique, as in four dimensions with an isoclinic rotation.
In n even dimensions (n = 2, 4, 6...) there are up to planes of rotation span the space, so a general rotation rotates all points except the origin which is the only fixed point. In n odd dimensions (n = 3, 5, 7, ...) there are planes and angles of rotation, the same as the even dimension one lower. These do not span the space, but leave an line which does not rotate – like the axis of rotation
in three dimensions, except rotations do not take place about this line but in multiple planes orthogonal to it.
s. Reflections can be specified in n-dimensions by giving an (n − 1)-dimensional subspace to reflect in, so a two-dimensional reflection is in a line, a three-dimensional reflection is in a plane, and so on. But this becomes increasingly difficult to apply in higher dimensions, so it is better to use vectors instead, as follows.
A reflection in n-dimensions is specified by a vector perpendicular to the (n − 1)-dimensional subspace. To generate simple rotations only reflections that fix the origin are needed, so the vector does not have a position, just direction. It does also not matter which way it is facing: it can be replaced with its negative without changing the result. Similarly unit vectors can be used to simplify the calculations.
So the reflection in a (n − 1)-dimensional space is given by the unit vector perpendicular to it, m, thus:
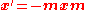
where the product is the geometric product from geometric algebra
.
If x' is reflected in another, distinct, (n − 1)-dimensional space, described by a unit vector n perpendicular to it, the result is
This is a simple rotation in n-dimensions, through twice the angle between the subspaces, which is also the angle between the vectors m and n. It can be checked using geometric algebra that this is a rotation, and that it rotates all vectors as expected.
The quantity mn is a rotor
, and nm is its inverse as
So the rotation can be written
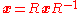
where R = mn is the rotor.
The plane of rotation is the plane containing m and n, which must be distinct otherwise the reflections are the same and no rotation takes place. As either vector can be replaced by its negative the angle between them can always be acute, or at most π/2. The rotation is through twice the angle between the vectors, up to π or a half-turn. The sense of the rotation is to rotate from m towards n: the geometric product is not commutative so the product nm is the inverse rotation, with sense from n to m.
Conversely all simple rotations can be generated this way, with two reflections, by two unit vectors in the plane of rotation separated by half the desired angle of rotation. These can be composed to produce more general rotations, using up to n reflections if the dimension n is even, n − 2 if n is odd, by choosing pairs of reflections given by two vectors in each plane of rotation.
s are quantities from geometric algebra
, clifford algebra
and the exterior algebra
, which generalise the idea of vectors into two dimensions. As vectors are to lines, so are bivectors to planes. So every plane (in any dimension) can be associated with a bivector, and every simple bivector is associated with a plane. This makes them a good fit for describing planes of rotation.
Every rotation plane in a rotation has a simple bivector associated with it. This is parallel to the plane and has magnitude equal to the angle of rotation in the plane. These bivectors are summed to produce a single, generally non-simple, bivector for the whole rotation. This can generate a rotor
through the exponential map
, which can be used to rotate an object.
Bivectors are related to rotors through the exponential map
(which applied to bivectors generates rotors and rotations using De Moivre's formula
). In particular given any bivector B the rotor associated with it is
This is a simple rotation if the bivector is simple, a more general rotation otherwise. When squared,
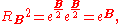
it gives a rotor that rotates through twice the angle. If B is simple then this is the same rotation as is generated by two reflections, as the product mn gives a rotation through twice the angle between the vectors. These can be equated,
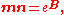
from which it follows that the bivector associated with the plane of rotation containing m and n that rotates m to n is
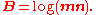
This is a simple bivector, associated with the simple rotation described. More general rotations in four or more dimensions are associated with sums of simple bivectors, one for each plane of rotation, calculated as above.
Examples include the two rotations in four dimensions given above. The simple rotation in the zw-plane by an angle θ has bivector e34θ, a simple bivector. The double rotation by α and β in the xy-plane and zw-planes has bivector e12α + e34β, the sum of two simple bivectors e12α and e34β which are parallel to the two planes of rotation and have magnitudes equal to the angles of rotation.
Given a rotor the bivector associated with it can be recovered by taking the logarithm of the rotor, which can then be split into simple bivectors to determine the planes of rotation, although in practice for all but the simplest of cases this may be impractical. But given the simple bivectors geometric algebra is a useful tool for studying planes of rotation using algebra like the above.
such pairs. These correspond to the planes of rotation, the eigenplane
s of the matrix, which can be calculated using algebraic techniques. In addition arguments of the complex roots are the magnitudes of the bivectors associated with the planes of rotations. The form of the characteristic equation is related to the planes, making it possible to relate its algebraic properties like repeated roots to the bivectors, where repeated bivector magnitudes have particular geometric interpretations.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a plane of rotation is an abstract object used to describe or visualise rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
s in space. In three dimensions it is an alternative to the axis of rotation
Rotation around a fixed axis
Rotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation around more than one axis at the same...
, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.
Mathematically such planes can be described in a number of ways. They can be described in terms of planes and angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s of rotation. They can be associated with bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s from geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
. They are related to the eigenvalues and eigenvectors of a rotation matrix. And in particular dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s they are related to other algebraic and geometric properties, which can then be generalised to other dimensions.
Planes of rotation are not used much in two and three dimensions, as in two dimensions there is only one plane so identifying the plane of rotation is trivial and rarely done, while in three dimensions the axis of rotation serves the same purpose and is the more established approach. The main use for them is in describing more complex rotations in higher dimensions, where they can be used to break down the rotations into simpler parts. This can be done using geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, with the planes of rotations associated with simple bivectors in the algebra.
Plane
For this article all planes are planes through the originOrigin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
, that is they contain the zero vector. Such a plane in n-dimensional space is a 2-dimensional linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of the space. It is completely specified by any two non-zero and non-parallel vectors that lie in the plane, that is by any two vectors a and b, such that
where ∧ is the exterior product from exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
or geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
(in three dimensions the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
can be used). More precisely the quantity a ∧ b is the bivector associated with the plane specifed by a and b, and has magnitude |a| |b| sin φ, where φ is the angle between the vectors; hence the requirement that the vectors be non-zero and non-parallel.
If the bivector a ∧ b is written B then the condition that a point lies on the plane associated with B is simply
This is true in all dimensions, and can be taken as the definition on the plane. In particular, from the properties of the exterior product it is satisfied by both a and b, and so by any vector of the form
with λ and μ real numbers. As λ and μ range over all real numbers c ranges over the whole plane, so this can be taken as another definition of the plane.
Plane of rotation
A plane of rotation for a particular rotationRotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
is a plane that is mapped to itself by the rotation. The plane is not fixed, but all vectors in the plane are mapped to other vectors in the same plane by the rotation. This transformation of the plane to itself is always a rotation about the origin, through an angle which is the angle of rotation
Angle of rotation
In mathematics, the angle of rotation is a measurement of the amount, the angle, that a figure is rotated about a fixed point, often the center of a circle....
for the plane.
Every rotation except for the identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
rotation (with matrix the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
) has at least one plane of rotation, and up to
planes of rotation, where n is the dimension. The maximum number of planes up to eight dimensions is shown in this table:
| Dimension | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| Number of planes | 1 | 1 | 2 | 2 | 3 | 3 | 4 |
When a rotation has multiple planes of rotation they are always orthogonal to each other, with only the origin in common. This is a stronger condition than to say the planes are at right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
s; it instead means that the planes have no nonzero vectors in common, and that every vector in one plane is orthogonal to every vector in the other plane. This can only happen in four or more dimensions. In two dimensions there is only one plane, while in three dimensions all planes have at least one nonzero vector in common, along their line of intersection.
In more than three dimensions planes of rotation are not always unique. For example the negative of the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
in four dimensions (the central inversion),
describes a rotation in four dimensions in which every plane through the origin is a plane of rotation through an angle π, so any pair of orthogonal planes generates the rotation. But for a general rotation it is at least theoretically possible to identify a unique set of orthogonal planes, in each of which points are rotated through an angle, so the set of planes and angles fully characterise the rotation.
Two dimensions
In two-dimensional spaceTwo-dimensional space
- Details :Bi-dimensional space is a geometric model of the planar projection of the physical universe in which we live.The two dimensions are commonly called length and width .Both directions lies in the same plane....
there is only one plane of rotation, the plane of the space itself. In a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
it is the Cartesian plane, in complex numbers it is the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. Any rotation therefore is of the whole plane, i.e. of the space, keeping only the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
fixed. It is specified completely by the signed angle of rotation, in the range for example −π to π. So if the angle is θ the rotation in the complex plane is given by Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
:
while the rotation in a Cartesian plane is given by the 2×2 rotation matrix:
Three dimensions
In three-dimensional spaceThree-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
there are an infinite number of planes of rotation, only one of which is involved in any given rotation. That is for a general rotation there is precisely one plane which is associated with it or which the rotation takes place in. The only exception is the trivial rotation, corresponding to the identity matrix, in which no rotation takes place.
In any rotation in three dimensions there is always a fixed axis, the axis of rotation. The rotation can described by giving this axis, with the angle through which the rotation turns about it; this is the axis angle
Axis angle
The axis-angle representation of a rotation, also known as the exponential coordinates of a rotation, parameterizes a rotation by two values: a unit vector indicating the direction of a directed axis , and an angle describing the magnitude of the rotation about the axis...
representation of a rotation. The plane of rotation is the plane orthogonal to this axis, so the axis is a surface normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
of the plane. The rotation then rotates this plane through the same angle as it rotates around the axis, that is everything in the plane rotates by the same angle about the origin.
One example is shown in the diagram, where the rotation takes place about the z-axis. The plane of rotation is the xy-plane, so everything in that plane it kept in the plane by the rotation. This could be described by a matrix like the following, with the rotation being through an angle θ (about the axis or in the plane):
North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is, subject to the caveats explained below, defined as the point in the northern hemisphere where the Earth's axis of rotation meets its surface...
and South Pole
South Pole
The South Pole, also known as the Geographic South Pole or Terrestrial South Pole, is one of the two points where the Earth's axis of rotation intersects its surface. It is the southernmost point on the surface of the Earth and lies on the opposite side of the Earth from the North Pole...
and the plane of rotation is the plane through the equator
Equator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
between the Northern
Northern Hemisphere
The Northern Hemisphere is the half of a planet that is north of its equator—the word hemisphere literally means “half sphere”. It is also that half of the celestial sphere north of the celestial equator...
and Southern
Southern Hemisphere
The Southern Hemisphere is the part of Earth that lies south of the equator. The word hemisphere literally means 'half ball' or "half sphere"...
Hemispheres. Other examples include mechanical devices like a gyroscope
Gyroscope
A gyroscope is a device for measuring or maintaining orientation, based on the principles of angular momentum. In essence, a mechanical gyroscope is a spinning wheel or disk whose axle is free to take any orientation...
or flywheel
Flywheel
A flywheel is a rotating mechanical device that is used to store rotational energy. Flywheels have a significant moment of inertia, and thus resist changes in rotational speed. The amount of energy stored in a flywheel is proportional to the square of its rotational speed...
which store rotational energy
Rotational energy
The rotational energy or angular kinetic energy is the kinetic energy due to the rotation of an object and is part of its total kinetic energy...
in mass usually along the plane of rotation.
In any three dimensional rotation the plane of rotation is uniquely defined. Together with the angle of rotation it fully describes the rotation. Or in a continuously rotating object the rotational properties such as the rate of rotation can be described in terms of the plane of rotation. It is perpendicular to, and so is defined by and defines, an axis of rotation, so any description of a rotation in terms of a plane of rotation can be described in terms of an axis of rotation, and vice-versa. But unlike the axis of rotation the plane generalises into other, in particular higher, dimensions.
Four dimensions
A general rotation in four-dimensional space has only one fixed point, the origin. Therefore an axis of rotation cannot be used in four dimensions. But planes of rotation can be used, and each non-trivial rotation in four dimensions has one or two planes of rotation.Simple rotations
A rotation with only one plane of rotation is a simple rotation. In a simple rotation there is a fixed plane, and rotation can be said to take place about this plane, so points as they rotate do not change their distance from this plane. The plane of rotation is orthogonal to this plane, and the rotation can be said to take place in this plane.For example the following matrix fixes the xy-plane: points in that plane and only in that plane are unchanged. The plane of rotation is the zw-plane, points in this plane are rotated through an angle θ. A general point rotates only in the zw-plane, that is it rotates around the xy-plane by changing only its z and w coordinates.
In two and three dimensions all rotations are simple, in that they have only one plane of rotation. Only in four and more dimensions are there rotations that are not simple simple rotations. In particular in four dimensions there are also double and isoclinic rotations.
Double rotations
In a double rotation there are two planes of rotation, no fixed planes, and the only fixed point is the origin. The rotation can be said to take place in both planes of rotation, as points in them are rotated within the planes. These planes are orthogonal, that is they have no vectors in common so every vector in one plane is at right angles to every vector in the other plane. The two rotation planes span four-dimensional space, so every point in the space can be specified by two points, one on each of the planes.A double rotation has two angles of rotation, one for each plane of rotation. The rotation is specified by giving the two planes and two non-zero angles, α and β (if either angle is zero the rotation is simple). Points in the first plane rotate through α, while points in the second plane rotate through β. All other points rotate through an angle between α and β, so in a sense they together determine the amount of rotation. For a general double rotation the planes of rotation and angles are unique, and given a general rotation they can be calculated. For example a rotation of α in the xy-plane and β in the zw-plane is given by the matrix
Isoclinic rotations
A special case of the double rotation is when the angles are equal, that is if . This is called an isoclinic rotation, and it differs from a general double rotation in a number of ways. For example in an isoclinic rotations all non-zero points rotate through the same angle, α. Most importantly the planes of rotation are not uniquely identified. There are instead an infinite number of pairs of orthogonal planes that can be treated as planes of rotation. For example any point can be taken, and the plane it rotates in together with the plane orthogonal to it can be used as two planes of rotation.Higher dimensions
As already noted the maximum number of planes of rotation in n dimensions is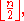so the complexity quickly increases with more than four dimensions and categorising rotations as above becomes too complex to be practical, but some observations can be made.
Simple rotations can be identified in all dimensions, as rotations with just one plane of rotation. A simple rotation in n dimensions takes place about (that is at a fixed distance from) an -dimensional subspace orthogonal to the plane of rotation.
A general rotation is not simple, and has the maximum number of planes of rotation as given above. In the general case the angles of rotations in these planes are distinct and the planes are uniquely defined. If any of the angles are the same then the planes are not unique, as in four dimensions with an isoclinic rotation.
In n even dimensions (n = 2, 4, 6...) there are up to planes of rotation span the space, so a general rotation rotates all points except the origin which is the only fixed point. In n odd dimensions (n = 3, 5, 7, ...) there are planes and angles of rotation, the same as the even dimension one lower. These do not span the space, but leave an line which does not rotate – like the axis of rotation
Rotation around a fixed axis
Rotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation around more than one axis at the same...
in three dimensions, except rotations do not take place about this line but in multiple planes orthogonal to it.
Mathematical properties
The examples given above were chosen to be clear and simple examples of rotations, with planes generally parallel to the coordinate axes in three and four dimensions. But this is not generally the case: planes are not usually parallel to the axes, and the matrices cannot simply be written down. In all dimensions the rotations are fully described by the planes of rotation and their associated angles, so it is useful to be able to determine them, or at least find ways to describe them mathematically.Reflections
Every simple rotation can be generated by two reflectionReflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s. Reflections can be specified in n-dimensions by giving an (n − 1)-dimensional subspace to reflect in, so a two-dimensional reflection is in a line, a three-dimensional reflection is in a plane, and so on. But this becomes increasingly difficult to apply in higher dimensions, so it is better to use vectors instead, as follows.
A reflection in n-dimensions is specified by a vector perpendicular to the (n − 1)-dimensional subspace. To generate simple rotations only reflections that fix the origin are needed, so the vector does not have a position, just direction. It does also not matter which way it is facing: it can be replaced with its negative without changing the result. Similarly unit vectors can be used to simplify the calculations.
So the reflection in a (n − 1)-dimensional space is given by the unit vector perpendicular to it, m, thus:
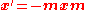
where the product is the geometric product from geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
.
If x' is reflected in another, distinct, (n − 1)-dimensional space, described by a unit vector n perpendicular to it, the result is
This is a simple rotation in n-dimensions, through twice the angle between the subspaces, which is also the angle between the vectors m and n. It can be checked using geometric algebra that this is a rotation, and that it rotates all vectors as expected.
The quantity mn is a rotor
Rotor (mathematics)
A rotor is an n-blade object in geometric algebra, which rotates another n-blade object about a fixed or translated point. They are normally motivated by considering an even number of reflections, which generate rotations...
, and nm is its inverse as
So the rotation can be written
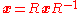
where R = mn is the rotor.
The plane of rotation is the plane containing m and n, which must be distinct otherwise the reflections are the same and no rotation takes place. As either vector can be replaced by its negative the angle between them can always be acute, or at most π/2. The rotation is through twice the angle between the vectors, up to π or a half-turn. The sense of the rotation is to rotate from m towards n: the geometric product is not commutative so the product nm is the inverse rotation, with sense from n to m.
Conversely all simple rotations can be generated this way, with two reflections, by two unit vectors in the plane of rotation separated by half the desired angle of rotation. These can be composed to produce more general rotations, using up to n reflections if the dimension n is even, n − 2 if n is odd, by choosing pairs of reflections given by two vectors in each plane of rotation.
Bivectors
BivectorBivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s are quantities from geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
and the exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
, which generalise the idea of vectors into two dimensions. As vectors are to lines, so are bivectors to planes. So every plane (in any dimension) can be associated with a bivector, and every simple bivector is associated with a plane. This makes them a good fit for describing planes of rotation.
Every rotation plane in a rotation has a simple bivector associated with it. This is parallel to the plane and has magnitude equal to the angle of rotation in the plane. These bivectors are summed to produce a single, generally non-simple, bivector for the whole rotation. This can generate a rotor
Rotor (mathematics)
A rotor is an n-blade object in geometric algebra, which rotates another n-blade object about a fixed or translated point. They are normally motivated by considering an even number of reflections, which generate rotations...
through the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
, which can be used to rotate an object.
Bivectors are related to rotors through the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
(which applied to bivectors generates rotors and rotations using De Moivre's formula
De Moivre's formula
In mathematics, de Moivre's formula , named after Abraham de Moivre, states that for any complex number x and integer n it holds that...
). In particular given any bivector B the rotor associated with it is
This is a simple rotation if the bivector is simple, a more general rotation otherwise. When squared,
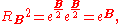
it gives a rotor that rotates through twice the angle. If B is simple then this is the same rotation as is generated by two reflections, as the product mn gives a rotation through twice the angle between the vectors. These can be equated,
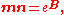
from which it follows that the bivector associated with the plane of rotation containing m and n that rotates m to n is
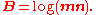
This is a simple bivector, associated with the simple rotation described. More general rotations in four or more dimensions are associated with sums of simple bivectors, one for each plane of rotation, calculated as above.
Examples include the two rotations in four dimensions given above. The simple rotation in the zw-plane by an angle θ has bivector e34θ, a simple bivector. The double rotation by α and β in the xy-plane and zw-planes has bivector e12α + e34β, the sum of two simple bivectors e12α and e34β which are parallel to the two planes of rotation and have magnitudes equal to the angles of rotation.
Given a rotor the bivector associated with it can be recovered by taking the logarithm of the rotor, which can then be split into simple bivectors to determine the planes of rotation, although in practice for all but the simplest of cases this may be impractical. But given the simple bivectors geometric algebra is a useful tool for studying planes of rotation using algebra like the above.
Eigenvalues and eigenplanes
The planes of rotations for a particular rotation using the eigenvalues. Given a general rotation matrix in n dimensions its characteristic equation has either one (in odd dimensions) or zero (in even dimensions) real roots. The other roots are in complex conjugate pairs, exactlysuch pairs. These correspond to the planes of rotation, the eigenplane
Eigenplane
In mathematics, an eigenplane is a two-dimensional invariant subspace in a given vector space. By analogy with the term eigenvector for a vector which, when operated on by a linear operator is another vector which is a scalar multiple of itself, the term eigenplane can be used to describe a...
s of the matrix, which can be calculated using algebraic techniques. In addition arguments of the complex roots are the magnitudes of the bivectors associated with the planes of rotations. The form of the characteristic equation is related to the planes, making it possible to relate its algebraic properties like repeated roots to the bivectors, where repeated bivector magnitudes have particular geometric interpretations.