Axis angle
Encyclopedia
The axis-angle representation of a rotation, also known as the exponential coordinates of a rotation, parameterizes a rotation
by two values: a unit vector indicating the direction of a directed axis (straight line), and an angle
describing the magnitude of the rotation about the axis. The rotation occurs in the sense prescribed by the right-hand rule
.
This representation evolves from Euler's rotation theorem
, which implies that any rotation or sequence of rotations of a rigid body in a three-dimensional space is equivalent to a pure rotation about a single fixed axis.
The axis-angle representation is equivalent to the more concise rotation vector, or Euler vector representation. In this case, both the axis and the angle are represented by a non-normalized vector codirectional with the axis whose magnitude
is the rotation angle.
Rodrigues' rotation formula
can be used to apply to a vector a rotation represented by an axis and an angle.
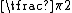radians (or 90 degrees
) about the z axis. In axis-angle representation, this would be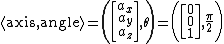
This can be represented as a rotation vector with a magnitude of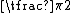
pointing in the z direction.
) is an efficient algorithm for rotating a vector in space, given a rotation axis and an angle of rotation
. In other words, the Rodrigues formula provides an algorithm to compute the exponential map
from so(3) to SO(3) without computing the full matrix exponent (the rotation matrix).
If v is a vector in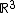
and ω is a unit vector describing an axis of rotation about which we want to rotate v by an angle θ (in a right-handed sense
), the Rodrigues formula to obtain the rotated vector is:
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
by two values: a unit vector indicating the direction of a directed axis (straight line), and an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
describing the magnitude of the rotation about the axis. The rotation occurs in the sense prescribed by the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
.
This representation evolves from Euler's rotation theorem
Euler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
, which implies that any rotation or sequence of rotations of a rigid body in a three-dimensional space is equivalent to a pure rotation about a single fixed axis.
The axis-angle representation is equivalent to the more concise rotation vector, or Euler vector representation. In this case, both the axis and the angle are represented by a non-normalized vector codirectional with the axis whose magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
is the rotation angle.
Rodrigues' rotation formula
Rodrigues' rotation formula
In the theory of three-dimensional rotation, Rodrigues' rotation formula is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix from an axis-angle representation...
can be used to apply to a vector a rotation represented by an axis and an angle.
Uses
The axis-angle representation is convenient when dealing with rigid body dynamics. It is useful to both characterize rotations, and also for converting between different representations of rigid body motion, such as homogeneous transformations and twists.Example
Say you are standing on the ground and you pick the direction of gravity to be the negative z direction. Then if you turn to your left, you will travel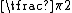 radians (or 90 degreesDegree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
) about the z axis. In axis-angle representation, this would be
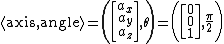
This can be represented as a rotation vector with a magnitude of
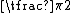pointing in the z direction.
Rotating a vector
Rodrigues' rotation formula (named after Olinde RodriguesOlinde Rodrigues
Benjamin Olinde Rodrigues , more commonly known as Olinde Rodrigues, was a French banker, mathematician, and social reformer.Rodrigues was born into a well-to-do Sephardi Jewish family in Bordeaux....
) is an efficient algorithm for rotating a vector in space, given a rotation axis and an angle of rotation
Angle of rotation
In mathematics, the angle of rotation is a measurement of the amount, the angle, that a figure is rotated about a fixed point, often the center of a circle....
. In other words, the Rodrigues formula provides an algorithm to compute the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
from so(3) to SO(3) without computing the full matrix exponent (the rotation matrix).
If v is a vector in
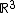and ω is a unit vector describing an axis of rotation about which we want to rotate v by an angle θ (in a right-handed senseRight-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
), the Rodrigues formula to obtain the rotated vector is:
-
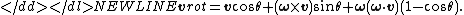
This is more efficient than converting ω and θ into a rotation matrix, and using the rotation matrix to compute the rotated vector.
Relationship to other representations
There are many ways to represent a rotation. It is useful to understand how different representations relate to one another, and how to convert between them.
Exponential map from so(3) to SO(3)
The exponential mapExponential mapIn differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
is used as a transformation from axis-angle representation of rotations to rotation matrices.
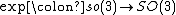
Essentially, by using a Taylor expansion you can derive a closed form relationship between these two representations. Given an axis,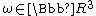
having length 1, and an angle, 
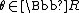, an equivalent rotation matrix is given by the following:
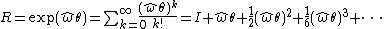
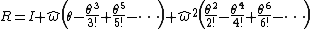
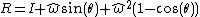
where R is a 3x3 rotation matrix and the hat operator gives the antisymmetric matrix equivalent of the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
. This can be easily derived from Rodrigues' rotation formulaRodrigues' rotation formulaIn the theory of three-dimensional rotation, Rodrigues' rotation formula is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix from an axis-angle representation...
.
Log map from SO(3) to so(3)
To retrieve the axis-angle representation of a rotation matrix calculate the angle of rotation: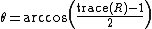
and then use it to find the normalized axis: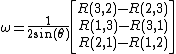
Note, also that the Matrix logarithm of the rotation matrix R is: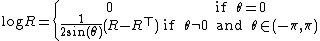
Except when R has eigenvalues equal to -1 where the log is not unique. However, even in the case where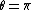
the Frobenius norm of the log is: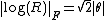
Note that given rotation matrices A and B: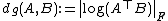
is the geodesic distance on the 3D manifold of rotation matrices.
Unit Quaternions
To transform from axis-angle coordinates to unit quaternions use the following expression:
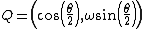
Given a unit quaternion, the axis-angle coordinates can be extracted using the following:
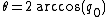
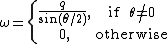
It may also be useful to know: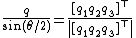
Simultaneous orthogonal rotations angle
Multiplying the rotation axis and angle gives vector SORA:
-
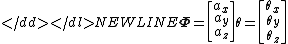
where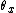
, 
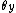, and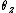 
represent angles of three simultaneous rotations around orthogonal axes. It holds:
-
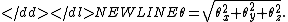
and
-
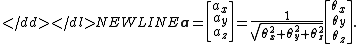
See also
- SO(3) - the group of all rotations in three dimensional space
- Charts on SO(3)Charts on SO(3)In mathematics, the special orthogonal group in three dimensions, otherwise known as the rotation group SO, is a naturally occurring example of a manifold. The various charts on SO set up rival coordinate systems: in this case there cannot be said to be a preferred set of parameters describing a...
for other representations - rotation groupRotation groupIn mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
- a mathematical look at rotations - homogeneous coordinatesHomogeneous coordinatesIn mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
- screw theoryScrew theoryScrew theory refers to the algebra and calculus of pairs of vectors, such as forces and moments and angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies....
- a representation of rigid body motions and velocities using the concepts of twists, screws and wrenches - Rotation around a fixed axisRotation around a fixed axisRotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation around more than one axis at the same...
- Rotation representation (mathematics)Rotation representation (mathematics)In geometry a rotation representation expresses a rotation as a mathematical transformation. In physics, this concept extends to classical mechanics where rotational kinematics is the science of describing with numbers the purely rotational motion of an object.According to Euler's rotation theorem...
- Rodrigues' rotation formulaRodrigues' rotation formulaIn the theory of three-dimensional rotation, Rodrigues' rotation formula is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix from an axis-angle representation...
- Simultaneous orthogonal rotations angleSimultaneous orthogonal rotations angleA simultaneous orthogonal rotations angle is a vector representing angular orientation of a rigid-body relative to some reference frame...
-
-
-