Details

Bi-dimensional space is a geometric model of the planar projection of the physical universe

Universe

The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...

 in which we live.
The two dimensions are commonly called length and width .Both directions lies in the same plane.

In physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

 and mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a sequence of n numbers

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 can be understood as a location

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

 in n-dimensional space. When n = 2, the set of all such locations is called 2-dimensional Euclidean space or bi-dimensional Euclidean space.

In physics, our bi-dimensional space is viewed as a planar representation of the space in which we move, described as bi-dimensional space or two-dimensional space

Two-dimensional space

- Details :Bi-dimensional space is a geometric model of the planar projection of the physical universe in which we live.The two dimensions are commonly called length and width .Both directions lies in the same plane....

.

Polytopes

In two dimensions, there are infinitely many regular polytopes: the polygons. The first few are shown below:

Convex

The Schläfli symbol {p} represents a regular p-gon

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

.

Name	Triangle (2-simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... )	Square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... (2-orthoplex Cross-polytope In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices... ) (2-cube Hypercube In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An... )	Pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...	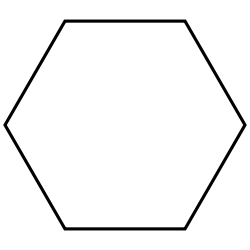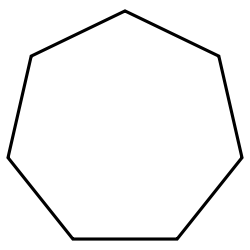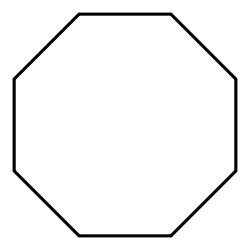Hexagon	Heptagon	Octagon
Schläfli	{3}	{4}	{5}	{6}	{7}	{8}
Image
Name	Nonagon	Decagon Decagon In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...	Hendecagon Hendecagon In geometry, a hendecagon is an 11-sided polygon....	Dodecagon Dodecagon In geometry, a dodecagon is any polygon with twelve sides and twelve angles.- Regular dodecagon :It usually refers to a regular dodecagon, having all sides of equal length and all angles equal to 150°...	Triskaidecagon	Tetradecagon
Schläfli	{9}	{10}	{11}	{12}	{13}	{14}
Image
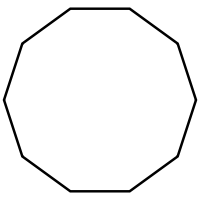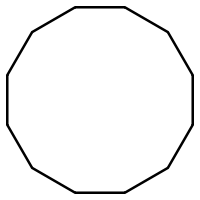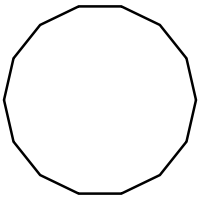Name	Pentadecagon Pentadecagon In geometry, a pentadecagon is any 15-sided, 15-angled, polygon.- Regular pentadecagon:A regular pentadecagon has interior angles of 156°, and with a side length a, has an area given by...	Hexadecagon Hexadecagon In mathematics, a hexadecagon is a polygon with 16 sides and 16 vertices.- Regular hexadecagon :A regular hexadecagon is constructible with a compass and straightedge....	Heptadecagon Heptadecagon In geometry, a heptadecagon is a seventeen-sided polygon.-Heptadecagon construction:The regular heptadecagon is a constructible polygon, as was shown by Carl Friedrich Gauss in 1796 at the age of 19....	Octadecagon Octadecagon An octadecagon is a polygon with 18 sides and 18 vertices. Another name for an octadecagon is octakaidecagon.- Construction :A regular octadecagon cannot be constructed using compass and straightedge.- Petrie polygons :...	Enneadecagon Enneadecagon In geometry, an enneadecagon is a polygon with 19 sides and angles. It is also known as an enneakaidecagon or a nonadecagon.The radius of the circumcircle of the regular enneadecagon with side length t is...	Icosagon Icosagon In geometry, an icosagon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.One interior angle in a regular icosagon is 162° meaning that one exterior angle would be 18°...	...n-gon Regular polygon A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
Schläfli	{15}	{16}	{17}	{18}	{19}	{20}	{n}
Image

Degenerate (Spherical)

The regular henagon {1} and regular digon

Digon

In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...

 {2} can be considered degenerate regular polygons. They can exist nondegenerately in non-Euclidean spaces like on the surface of a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

 or torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

.

Name	Henagon	Digon Digon In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...
Schläfli	{1}	{2}
Image

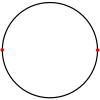Non-convex

There exist infinitely many non-convex regular polytopes in two dimensions, whose Schläfli symbols consist of rational numbers {n/m}. They are called star polygons and share the same vertex arrangement

Vertex arrangement

In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....

s of the convex regular polygons.

In general, for any natural number n, there are n-pointed non-convex regular polygonal stars with Schläfli symbols {n/m} for all m such that m < n/2 (strictly speaking {n/m}={n/(n-m)}) and m and n are coprime

Coprime

In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...

.

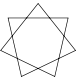
Name	Pentagram Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes...	Heptagram Heptagram A heptagram or septegram is a seven-pointed star drawn with seven straight strokes.- Geometry :In general, a heptagram is any self-intersecting heptagon .... s		Octagram Octagram In geometry, an octagram is an eight-sided star polygon.- Geometry :In general, an octagram is any self-intersecting octagon ....	Enneagrams Enneagram (geometry) In geometry, an enneagram is a nine-pointed geometric figure. It is sometimes called a nonagram.-Regular enneagram:A regular enneagram is constructed using the same points as the regular enneagon but connected in fixed steps...		Decagram	...n-agrams
Schläfli	{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}	{10/3}	{n/m}
Image

Hypersphere

The hypersphere

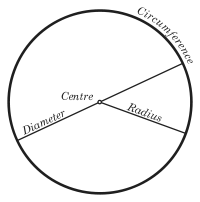
Hypersphere

In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...

 in 2 dimensions is a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

, sometimes called a 1-sphere because its surface is one-dimensional. Its area is
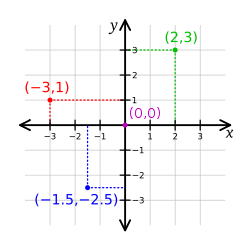
where is the radius.

Coordinate systems in two-dimensional space

The most popular coordinate systems are the Cartesian coordinate system

Cartesian coordinate system

A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...

, the polar coordinate system

Polar coordinate system

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....

 and the geographic coordinate system

Geographic coordinate system

A geographic coordinate system is a coordinate system that enables every location on the Earth to be specified by a set of numbers. The coordinates are often chosen such that one of the numbers represent vertical position, and two or three of the numbers represent horizontal position...

.