In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a decagon is any polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

 with ten sides and ten angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

s, and usually refers to a regular

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

 decagon, having all sides of equal length and each internal angle equal to 144°. Its Schläfli symbol is {10}.

Regular decagon

The area

Area

Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

 of a regular decagon is: (with t = edge length)



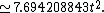
An alternative formula is 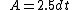where d is the distance between parallel sides, or the height when the decagon stands on one side as base.

By simple trigonometry d = 2t(cos54° + cos18°).

Sides

The side of a regular decagon inscribed in a unit circle is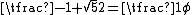 , where 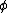is the golden ratio

Golden ratio

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...

, .

Construction

A regular decagon is constructible

Constructible polygon

In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not....

 using compass and straightedge

Compass and straightedge

Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....

:
An alternative (but similar) method is as follows:

1. Construct a pentagon in a circle by one of the methods shown in constructing a pentagon
   Pentagon
   In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
   
   .
2. Extend a line from each vertex of the pentagon through the center of the circle
   Circle
   A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
   
    to the opposite side of that same circle. Where each line cuts the circle is a vertex of the decagon.
3. The five corners of the pentagon constitute alternate corners of the decagon. Join these points to the adjacent new points to form the decagon..

Related figures

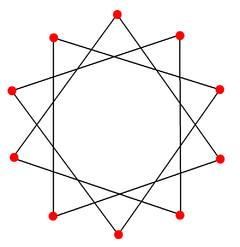
There is one regular star polygon, the decagram

Decagram

Decagram may refer to:* 10 grams, unit of mass* Decagram , geometric figure...

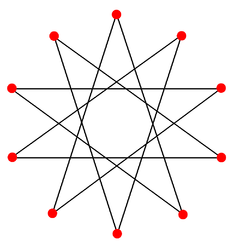
 {10/3}, using the same points, but connecting every third points. There are also two compounds: {10/4} is reduced to 2{5/2} as two pentagram

Pentagram

A pentagram is the shape of a five-pointed star drawn with five straight strokes...

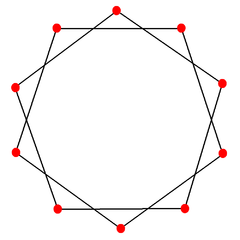
s, and {10/2} is reduced to 2{5} as two pentagon

Pentagon

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...

s.

{10/3} Decagram Decagram Decagram may refer to:* 10 grams, unit of mass* Decagram , geometric figure...

{10/2} or 2{5}

{10/4} or 2{5/2}

Petrie polygons

The regular decagon is the Petrie polygon

Petrie polygon

In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets...

 for many higher dimensional polytopes, shown in these skew orthogonal projections in various Coxeter planes:

A9	9-simplex	Rectified 9-simplex Rectified 9-simplex In nine-dimensional geometry, a rectified 9-simplex is a convex uniform 9-polytope, being a rectification of the regular 9-simplex.These polytopes are part of a family of 271 uniform 9-polytopes with A9 symmetry....	Trirectified 9-simplex	Quadrirectified 9-simplex	Quintirectified 9-simplex
BC5	5-orthoplex	Rectified 5-orthoplex	Birectified 5-cube	Rectified 5-cube Rectified 5-cube In give-dimensional geometry, a rectified 5-cube is a convex uniform 5-polytope, being a rectification of the regular 5-cube.There are 5 degrees of rectifications of a 5-polytope, the zeroth here being the 5-cube, and the 4th and last being the 5-orthoplex. Vertices of the rectified 5-cube are...	5-cube
D6	t1(431)	t3(131)	t2(131)	t1(131)	6-demicube (131)
H3	Dodecahedron	Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....	Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...

External links

• Definition and properties of a decagon With interactive animation