Icosahedron
Encyclopedia
In geometry
, an icosahedron (icon or aɪ; plural: -drons, -dra /-drə/; , from eikosi twenty + hedron seat) is a regular polyhedron
with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solid
s.
It has five triangular faces meeting at each vertex. It can be represented by its vertex figure
as 3.3.3.3.3 or 35, and also by Schläfli symbol {3,5}. It is the dual
of the dodecahedron, which is represented by {5,3}, having three pentagonal faces around each vertex.
 , the radius
, the radius
of a circumscribed sphere
(one that touches the icosahedron at all vertices) is
and the radius of an inscribed sphere (tangent
to each of the icosahedron's faces) is
while the midradius, which touches the middle of each edge, is
where (also called
(also called  ) is the golden ratio
) is the golden ratio
.
V of a regular icosahedron of edge length a are:

 The following Cartesian coordinates define the vertices of an icosahedron with edge-length 2, centered at the origin:
The following Cartesian coordinates define the vertices of an icosahedron with edge-length 2, centered at the origin:
where φ = (1+√5)/2 is the golden ratio (also written τ).
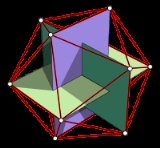
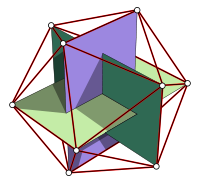
Note that these vertices form five sets of three concentric, mutually orthogonal golden rectangles, whose edges form Borromean rings
.
If the original icosahedron has edge length 1, its dual dodecahedron has edge length , one divided by the golden ratio
, one divided by the golden ratio
.
The 12 edges of a regular octahedron
can be subdivided in the golden ratio so that the resulting vertices define a regular icosahedron. This is done by first placing vectors along the octahedron's edges such that each face is bounded by a cycle, then similarly subdividing each edge into the golden mean along the direction of its vector. The five octahedra
defining any given icosahedron form a regular polyhedral compound
, as do the two icosahedra that can be defined in this way from any given octahedron.
 necessary in more elementary approaches.
necessary in more elementary approaches.
The existence of the icosahedron amounts to the existence of six equiangular lines
in . Indeed, intersecting such a system of equiangular lines with a Euclidean sphere centered at their common intersection yields the twelve vertices of a regular icosahedron as can easily be checked. Conversely, supposing the existence of a regular icosahedron, lines defined by its six pairs of opposite vertices form an equiangular system.
. Indeed, intersecting such a system of equiangular lines with a Euclidean sphere centered at their common intersection yields the twelve vertices of a regular icosahedron as can easily be checked. Conversely, supposing the existence of a regular icosahedron, lines defined by its six pairs of opposite vertices form an equiangular system.
In order to construct such an equiangular system, we start with this square matrix
square matrix
:

A straightforward computation yields (where
(where  is the 6x6 identity matrix). This implies that
is the 6x6 identity matrix). This implies that  has eigenvalues
has eigenvalues
 and
and  , both with multiplicity 3 since
, both with multiplicity 3 since  is symmetric and of trace
is symmetric and of trace
zero.
The matrix induces thus an Euclidean structure
induces thus an Euclidean structure
on the quotient space
 which is isomorphic
which is isomorphic
to since the kernel
since the kernel  of
of  has dimension
has dimension
3. The image under the projection
 of the six coordinate axes
of the six coordinate axes  in
in  forms thus a system of six equiangular lines in
forms thus a system of six equiangular lines in  intersecting pairwise at a common acute angle of
intersecting pairwise at a common acute angle of  . Orthogonal projection of
. Orthogonal projection of  onto the
onto the  -eigenspace
-eigenspace
of yields thus the twelve vertices of the icosahedron.
yields thus the twelve vertices of the icosahedron.
A second straightforward construction of the icosahedron uses representation theory
of the alternating group acting by direct isometries
acting by direct isometries
on the icosahedron.
of the regular icosahedron is isomorphic to the alternating group on five letters. This non-abelian
simple group
is the only non-trivial normal subgroup
of the symmetric group
on five letters. Since the Galois group
of the general quintic equation
is isomorphic to the symmetric group on five letters, and this normal subgroup is simple and non-abelian, the general quintic equation does not have a solution in radicals. The proof of the Abel-Ruffini theorem uses this simple fact, and Felix Klein
wrote a book that made use of the theory of icosahedral symmetries to derive an analytical solution to the general quintic equation, . See icosahedral symmetry: related geometries for further history, and related symmetries on seven and eleven letters.
The full symmetry group of the icosahedron (including reflections) is known as the full icosahedral group, and is isomorphic to the product of the rotational symmetry group and the group of size two, which is generated by the reflection through the center of the icosahedron.
of size two, which is generated by the reflection through the center of the icosahedron.
, 59 stellation
s were identified for the regular icosahedron. The first form is the icosahedron itself. One is a regular Kepler-Poinsot polyhedron. Three are regular compound polyhedra.
under the same rotation
s as the tetrahedron, and are somewhat analogous to the snub cube
and snub dodecahedron
, including some forms which are chiral
and some with Th-symmetry, i.e. have different planes of symmetry from the tetrahedron. The icosahedron has a large number of stellations, including one of the Kepler-Poinsot polyhedra and some of the regular compounds, which could be discussed here.
The icosahedron is unique among the Platonic solids in possessing a dihedral angle
greater than 120°. Its dihedral angle is approximately 138.19°. Thus, just as hexagons have angles not less than 120° and cannot be used alone as the faces of a convex regular polyhedron, because such a construction would not meet the requirement that at least three faces meet at a vertex and leave a positive defect
for folding in three dimensions, icosahedra cannot be used as the cells
of a convex regular polychoron
because, similarly, at least three cells must meet at an edge and leave a positive defect for folding in four dimensions (in general for a convex polytope
in n dimensions, at least three facets
must meet at a peak
and leave a positive defect for folding in n-space). However, when combined with suitable cells having smaller dihedral angles, icosahedra can be used as cells in semi-regular polychora (for example the snub 24-cell
), just as hexagons can be used as faces in semi-regular polyhedra (for example the truncated icosahedron
). Finally, non-convex polytopes do not carry the same strict requirements as convex polytopes, and icosahedra are indeed the cells of the icosahedral 120-cell, one of the ten non-convex regular polychora.
An icosahedron can also be called a gyroelongated pentagonal bipyramid. It can be decomposed into a gyroelongated pentagonal pyramid
and a pentagonal pyramid
or into a pentagonal antiprism
and two equal pentagonal pyramids.
s of the icosahedron. These colorings can be represented as 11213, 11212, 11111, naming the 5 triangular faces around each vertex by their color.
The icosahedron can be considered a snub tetrahedron, as snubification
of a regular tetrahedron gives a regular icosahedron having chiral tetrahedral symmetry
. It can also be constructed as an alternated truncated octahedron, having pyritohedral symmetry.
sequence into its dual
, the dodecahedron:
This polyhedron is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane
.
The icosahedron shares its vertex arrangement
with three Kepler-Poinsot solid
s. The great dodecahedron also has the same edge arrangement.
The icosahedron can tessellate hyperbolic space in the order-3 icosahedral honeycomb, with 3 icosahedra around each edge, 12 icosahedra around each vertex, with Schläfli symbol {3,5,3}. It is one of four regular tessellations in the hyperbolic 3-space.
polyhedra and tilings with vertex figure (3.3.3.3.p) and Coxeter-Dynkin diagram
. These face-transitive figures have (n32) rotational symmetry.

 Many virus
Many virus
es, e.g. herpes virus, have icosahedral shells
. Viral structures are built of repeated identical protein
subunits known as capsomere
s, and the icosahedron is the easiest shape to assemble using these subunits. A regular polyhedron is used because it can be built from a single basic unit protein used over and over again; this saves space in the viral genome
.
Various bacterial organelles with an icosahedral shape were also found. The icosahedral shell encapsulating enzymes and labile intermediates are built of different types of proteins with BMC domain
s.
In 1904, Ernst Haeckel
described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel's illustration for this radiolarian appears in the article on regular polyhedra.
The closo-carboranes are chemical compounds with shape very close to isosahedron. Icosahedral twinning
also occurs in crystals, especially nanoparticle
s.
In several roleplaying games, such as Dungeons & Dragons
, the twenty-sided die (d20 for short) is commonly used in determining success or failure of an action. This die is in the form of a regular icosahedron. It may be numbered from "0" to "9" twice (in which form it usually serves as a ten-sided die, or d10), but most modern versions are labeled from "1" to "20". See d20 System
.
R. Buckminster Fuller and Japanese cartographer Shoji Sadao designed a world map in the form of an unfolded icosahedron, called the Fuller projection, whose maximum distortion is only 2%.
An icosahedron is the three-dimensional game board for Icosagame, formerly known as the Ico Crystal Game.
An icosahedron is used in the board game Scattergories
to choose a letter of the alphabet. Six letters are omitted (Q, U, V, X, Y, and Z).
Inside a Magic 8-Ball
, various answers to yes-no question
s are inscribed on a regular icosahedron.
The "Sol de la Flor" light shade consists of twenty panels, which meet at the corners of an icosahedron in rosette
s resembling the overlapping petals of a frangipani flower.
Many borides
and allotropes of boron
contain boron B12 icosahedron as a basic structure unit.
If each edge of an icosahedron is replaced by a one ohm resistor
, the resistance between opposite vertices is 0.5 ohms, and that between adjacent vertices 11/30 ohms.
The company logo of the TDK Corporation
contains a geometric figure which is based on the stellation diagram of the icosahedron.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an icosahedron (icon or aɪ; plural: -drons, -dra /-drə/; , from eikosi twenty + hedron seat) is a regular polyhedron
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s.
It has five triangular faces meeting at each vertex. It can be represented by its vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
as 3.3.3.3.3 or 35, and also by Schläfli symbol {3,5}. It is the dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of the dodecahedron, which is represented by {5,3}, having three pentagonal faces around each vertex.
Dimensions
If the edge length of a regular icosahedron is , the radius
, the radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of a circumscribed sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
(one that touches the icosahedron at all vertices) is
and the radius of an inscribed sphere (tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to each of the icosahedron's faces) is
while the midradius, which touches the middle of each edge, is
where
 (also called
(also called  ) is the golden ratio
) is the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
.
Area and volume
The surface area A and the volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
V of a regular icosahedron of edge length a are:


Cartesian coordinates

- (0, ±1, ±φ)
- (±1, ±φ, 0)
- (±φ, 0, ±1)
where φ = (1+√5)/2 is the golden ratio (also written τ).
Note that these vertices form five sets of three concentric, mutually orthogonal golden rectangles, whose edges form Borromean rings
Borromean rings
In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...
.
If the original icosahedron has edge length 1, its dual dodecahedron has edge length
 , one divided by the golden ratio
, one divided by the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
.
The 12 edges of a regular octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
can be subdivided in the golden ratio so that the resulting vertices define a regular icosahedron. This is done by first placing vectors along the octahedron's edges such that each face is bounded by a cycle, then similarly subdividing each edge into the golden mean along the direction of its vector. The five octahedra
Compound of five octahedra
This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a stellation :It is the second stellation of the icosahedron, and given as Wenninger model index 23....
defining any given icosahedron form a regular polyhedral compound
Polyhedral compound
A polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram....
, as do the two icosahedra that can be defined in this way from any given octahedron.
Other facts
- It has 43,380 distinct netsNet (polyhedron)In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron...
. - To color the icosahedron, such that no two adjacent faces have the same color, requires at least 3 colors.
- When an icosahedron is inscribed in a sphere, it occupies less of the sphere's volume (60.54%) than a dodecahedron inscribed in the same sphere (66.49%).
Construction by a system of equiangular lines
The following construction of the icosahedron avoids tedious computations in the number fieldAlgebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
 necessary in more elementary approaches.
necessary in more elementary approaches.The existence of the icosahedron amounts to the existence of six equiangular lines
Equiangular lines
In geometry, a set of lines in Euclidean space is called equiangular if every pair of lines makes the same angle.Equiangular lines are related to two-graphs....
in
 . Indeed, intersecting such a system of equiangular lines with a Euclidean sphere centered at their common intersection yields the twelve vertices of a regular icosahedron as can easily be checked. Conversely, supposing the existence of a regular icosahedron, lines defined by its six pairs of opposite vertices form an equiangular system.
. Indeed, intersecting such a system of equiangular lines with a Euclidean sphere centered at their common intersection yields the twelve vertices of a regular icosahedron as can easily be checked. Conversely, supposing the existence of a regular icosahedron, lines defined by its six pairs of opposite vertices form an equiangular system.In order to construct such an equiangular system, we start with this
 square matrix
square matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
:

A straightforward computation yields
 (where
(where  is the 6x6 identity matrix). This implies that
is the 6x6 identity matrix). This implies that  has eigenvalues
has eigenvaluesEigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
 and
and  , both with multiplicity 3 since
, both with multiplicity 3 since  is symmetric and of trace
is symmetric and of traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
zero.
The matrix
 induces thus an Euclidean structure
induces thus an Euclidean structureEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
on the quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
 which is isomorphic
which is isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to
 since the kernel
since the kernel  of
of  has dimension
has dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
3. The image under the projection
Projection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
 of the six coordinate axes
of the six coordinate axes  in
in  forms thus a system of six equiangular lines in
forms thus a system of six equiangular lines in  intersecting pairwise at a common acute angle of
intersecting pairwise at a common acute angle of  . Orthogonal projection of
. Orthogonal projection of  onto the
onto the  -eigenspace
-eigenspaceEigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
of
 yields thus the twelve vertices of the icosahedron.
yields thus the twelve vertices of the icosahedron.A second straightforward construction of the icosahedron uses representation theory
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the alternating group
 acting by direct isometries
acting by direct isometriesIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
on the icosahedron.
Symmetry
The rotational symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the regular icosahedron is isomorphic to the alternating group on five letters. This non-abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
is the only non-trivial normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on five letters. Since the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of the general quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
is isomorphic to the symmetric group on five letters, and this normal subgroup is simple and non-abelian, the general quintic equation does not have a solution in radicals. The proof of the Abel-Ruffini theorem uses this simple fact, and Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
wrote a book that made use of the theory of icosahedral symmetries to derive an analytical solution to the general quintic equation, . See icosahedral symmetry: related geometries for further history, and related symmetries on seven and eleven letters.
The full symmetry group of the icosahedron (including reflections) is known as the full icosahedral group, and is isomorphic to the product of the rotational symmetry group and the group
 of size two, which is generated by the reflection through the center of the icosahedron.
of size two, which is generated by the reflection through the center of the icosahedron.Stellations
According to specific rules defined in the book The fifty nine icosahedraThe fifty nine icosahedra
The Fifty Nine Icosahedra is a book written and illustrated by H. S. M. Coxeter, P. Du Val, H. T. Flather and J. F. Petrie. It enumerates the stellations of the regular convex or Platonic icosahedron, according to a set of rules put forward by J. C. P. Miller...
, 59 stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
s were identified for the regular icosahedron. The first form is the icosahedron itself. One is a regular Kepler-Poinsot polyhedron. Three are regular compound polyhedra.
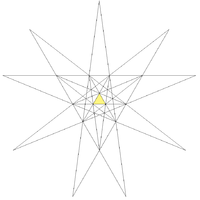 The faces of the icosahedron extended outwards as planes intersect, defining regions in space as shown by this stellation diagram Stellation diagram In geometry, a stellation diagram or stellation pattern is a two-dimensional diagram in the plane of some face of a polyhedron, showing lines where other face planes intersect with this one. The lines cause 2D space to be divided up into regions. Regions not intersected by any further lines are... of the intersections in a single plane. |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
Geometric relations
There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform. These are invariantInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under the same rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s as the tetrahedron, and are somewhat analogous to the snub cube
Snub cube
In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...
and snub dodecahedron
Snub dodecahedron
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....
, including some forms which are chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
and some with Th-symmetry, i.e. have different planes of symmetry from the tetrahedron. The icosahedron has a large number of stellations, including one of the Kepler-Poinsot polyhedra and some of the regular compounds, which could be discussed here.
The icosahedron is unique among the Platonic solids in possessing a dihedral angle
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
greater than 120°. Its dihedral angle is approximately 138.19°. Thus, just as hexagons have angles not less than 120° and cannot be used alone as the faces of a convex regular polyhedron, because such a construction would not meet the requirement that at least three faces meet at a vertex and leave a positive defect
Defect (geometry)
In geometry, the defect means the failure of some angles to add up to the expected amount of 360° or 180°, when such angles in the plane would...
for folding in three dimensions, icosahedra cannot be used as the cells
Cell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
of a convex regular polychoron
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
because, similarly, at least three cells must meet at an edge and leave a positive defect for folding in four dimensions (in general for a convex polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
in n dimensions, at least three facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
must meet at a peak
Peak (geometry)
In geometry, a peak is an -face of an n-dimensional polytope. A peak attaches at least three facets ....
and leave a positive defect for folding in n-space). However, when combined with suitable cells having smaller dihedral angles, icosahedra can be used as cells in semi-regular polychora (for example the snub 24-cell
Snub 24-cell
In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices....
), just as hexagons can be used as faces in semi-regular polyhedra (for example the truncated icosahedron
Truncated icosahedron
In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....
). Finally, non-convex polytopes do not carry the same strict requirements as convex polytopes, and icosahedra are indeed the cells of the icosahedral 120-cell, one of the ten non-convex regular polychora.
An icosahedron can also be called a gyroelongated pentagonal bipyramid. It can be decomposed into a gyroelongated pentagonal pyramid
Gyroelongated pentagonal pyramid
In geometry, the gyroelongated pentagonal pyramid is one of the Johnson solids . As its name suggests, it is formed by taking a pentagonal pyramid and "gyroelongating" it, which in this case involves joining a pentagonal antiprism to its base....
and a pentagonal pyramid
Pentagonal pyramid
In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point . Like any pyramid, it is self-dual....
or into a pentagonal antiprism
Pentagonal antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...
and two equal pentagonal pyramids.
Uniform colorings and subsymmetries
There are 3 uniform coloringUniform coloring
In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive...
s of the icosahedron. These colorings can be represented as 11213, 11212, 11111, naming the 5 triangular faces around each vertex by their color.
The icosahedron can be considered a snub tetrahedron, as snubification
Snub (geometry)
In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided...
of a regular tetrahedron gives a regular icosahedron having chiral tetrahedral symmetry
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
. It can also be constructed as an alternated truncated octahedron, having pyritohedral symmetry.
| Name | Regular icosahedron | alternated truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
snub Snub (geometry) In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided... tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
Pentagonal gyroelongated bipyramid Gyroelongated bipyramid In geometry, the gyroelongated bipyramids are an infinite set of polyhedra, constructed by elongating an n-gonal bipyramid by inserting an n-gonal antiprism between its congruent halves.- Forms :... |
|---|---|---|---|---|
| Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||||
| Schläfli symbol | {3,5} | h0,1{3,4} | s{3,3} | |
| Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles.... |
5 | 3 2 | | 3 3 2 | ||
| Symmetry | Ih [5,3] (*532) |
Th [3+,4] (3*2) |
T [3,3]+ (332) |
D5d [2+,10] (2*5) |
| Symmetry order | 60 | 24 | 12 | 10 |
| Uniform coloring Uniform coloring In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive... |
 (11111) |
 (11212) |
 (11213) |
(11122)&(22222) |
Related polyhedra and polytopes
The icosahedron can be transformed by a truncationTruncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
sequence into its dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
, the dodecahedron:
| Picture |  Dodecahedron |
 Truncated dodecahedron Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... |
 Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
 Truncated icosahedron Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
 Icosahedron |
|---|---|---|---|---|---|
| Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
This polyhedron is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
.
 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
 {3,4} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 {3,5} |
 {3,6} |
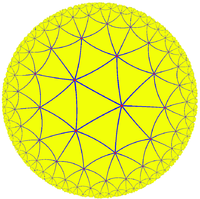 {3,7} |
 {3,8} |
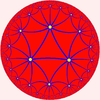 {3,9} |
The icosahedron shares its vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
with three Kepler-Poinsot solid
Kepler-Poinsot solid
In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra. They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures....
s. The great dodecahedron also has the same edge arrangement.
| Picture |  Great dodecahedron |
 Small stellated dodecahedron |
 Great icosahedron |
|---|---|---|---|
| Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
The icosahedron can tessellate hyperbolic space in the order-3 icosahedral honeycomb, with 3 icosahedra around each edge, 12 icosahedra around each vertex, with Schläfli symbol {3,5,3}. It is one of four regular tessellations in the hyperbolic 3-space.
 It is shown here as an edge framework in a Poincaré disk model Poincaré disk model In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk... , with one icosahedron visible in the center. |
Related polyhedra and tilings
The regular icosahedron, seen as a snub tetrahedron, is part of sequence of snubbedSnub (geometry)
In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided...
polyhedra and tilings with vertex figure (3.3.3.3.p) and Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
. These face-transitive figures have (n32) rotational symmetry.
 (3.3.3.3.3) (332) |
 (3.3.3.3.4) Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... (432) |
 (3.3.3.3.5) Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... (532) |
 3.3.3.3.6 Snub hexagonal tiling In geometry, the Snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex... (632) |
 3.3.3.3.7 (732) |
 3.3.3.3.8 (832) |
Uses and natural forms


Virus
A virus is a small infectious agent that can replicate only inside the living cells of organisms. Viruses infect all types of organisms, from animals and plants to bacteria and archaea...
es, e.g. herpes virus, have icosahedral shells
Capsid
A capsid is the protein shell of a virus. It consists of several oligomeric structural subunits made of protein called protomers. The observable 3-dimensional morphological subunits, which may or may not correspond to individual proteins, are called capsomeres. The capsid encloses the genetic...
. Viral structures are built of repeated identical protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
subunits known as capsomere
Capsomere
The capsomere is a basic subunit of the capsid, an outer covering of protein that protects the genetic material of a virus. Capsomeres self-assemble to form the capsid....
s, and the icosahedron is the easiest shape to assemble using these subunits. A regular polyhedron is used because it can be built from a single basic unit protein used over and over again; this saves space in the viral genome
Genome
In modern molecular biology and genetics, the genome is the entirety of an organism's hereditary information. It is encoded either in DNA or, for many types of virus, in RNA. The genome includes both the genes and the non-coding sequences of the DNA/RNA....
.
Various bacterial organelles with an icosahedral shape were also found. The icosahedral shell encapsulating enzymes and labile intermediates are built of different types of proteins with BMC domain
BMC domain
Bacterial Microcompartment domain is a protein domain found in a variety of shell proteins, including CsoS1A, CsoS1B and CsoS1C of Thiobacillus neapolitanus and their orthologs from other bacteria. These shell proteins form the polyhedral structure of organelle that play a metabolic role in...
s.
In 1904, Ernst Haeckel
Ernst Haeckel
The "European War" became known as "The Great War", and it was not until 1920, in the book "The First World War 1914-1918" by Charles à Court Repington, that the term "First World War" was used as the official name for the conflict.-Research:...
described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel's illustration for this radiolarian appears in the article on regular polyhedra.
The closo-carboranes are chemical compounds with shape very close to isosahedron. Icosahedral twinning
Crystal twinning
Crystal twinning occurs when two separate crystals share some of the same crystal lattice points in a symmetrical manner. The result is an intergrowth of two separate crystals in a variety of specific configurations. A twin boundary or composition surface separates the two crystals....
also occurs in crystals, especially nanoparticle
Nanoparticle
In nanotechnology, a particle is defined as a small object that behaves as a whole unit in terms of its transport and properties. Particles are further classified according to size : in terms of diameter, coarse particles cover a range between 10,000 and 2,500 nanometers. Fine particles are sized...
s.
In several roleplaying games, such as Dungeons & Dragons
Dungeons & Dragons
Dungeons & Dragons is a fantasy role-playing game originally designed by Gary Gygax and Dave Arneson, and first published in 1974 by Tactical Studies Rules, Inc. . The game has been published by Wizards of the Coast since 1997...
, the twenty-sided die (d20 for short) is commonly used in determining success or failure of an action. This die is in the form of a regular icosahedron. It may be numbered from "0" to "9" twice (in which form it usually serves as a ten-sided die, or d10), but most modern versions are labeled from "1" to "20". See d20 System
D20 System
The d20 System is a role-playing game system published in 2000 by Wizards of the Coast originally developed for the third edition of Dungeons & Dragons...
.
R. Buckminster Fuller and Japanese cartographer Shoji Sadao designed a world map in the form of an unfolded icosahedron, called the Fuller projection, whose maximum distortion is only 2%.
An icosahedron is the three-dimensional game board for Icosagame, formerly known as the Ico Crystal Game.
An icosahedron is used in the board game Scattergories
Scattergories
Scattergories is a creative-thinking category-based party game produced by Hasbro through the Milton Bradley Company and published in 1988...
to choose a letter of the alphabet. Six letters are omitted (Q, U, V, X, Y, and Z).
Inside a Magic 8-Ball
Magic 8-ball
The Magic 8 Ball is a toy used for fortune-telling or seeking advice, manufactured by Mattel.-Origin:While Magic 8-Ball did not exist in its current form until 1950, the functional component was invented by Albert C. Carter, who was inspired by a "spirit writing" device used by his mother, Mary, a...
, various answers to yes-no question
Yes-no question
In linguistics, a yes–no question, formally known as a polar question, is a question whose expected answer is either "yes" or "no". Formally, they present an exclusive disjunction, a pair of alternatives of which only one is acceptable. In English, such questions can be formed in both positive...
s are inscribed on a regular icosahedron.
The "Sol de la Flor" light shade consists of twenty panels, which meet at the corners of an icosahedron in rosette
Rosette (design)
A rosette is a round, stylized flower design, used extensively in sculptural objects from antiquity. Appearing in Mesopotamia and used to decorate the funeral stele in Ancient Greece...
s resembling the overlapping petals of a frangipani flower.
Many borides
Crystal structure of boron-rich metal borides
Metals, and specifically rare-earth elements , form numerous chemical complexes with boron. Their crystal structure and chemical bonding depend strongly on the metal element M and on its atomic ratio to boron. When B/M ratio exceeds 12, boron atoms form B12 icosahedra which are linked into a...
and allotropes of boron
Allotropes of boron
Elemental boron can exist in several allotropes, the most common of which are crystalline boron and brown amorphous boron. Crystalline boron has four major polymorphs: α, β, γ and T...
contain boron B12 icosahedron as a basic structure unit.
If each edge of an icosahedron is replaced by a one ohm resistor
Resistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
, the resistance between opposite vertices is 0.5 ohms, and that between adjacent vertices 11/30 ohms.
The company logo of the TDK Corporation
TDK
, formerly , is a Japanese company which manufactures electronic materials, electronic components, and recording and data-storage media, and markets them globally. Their motto is "Contribute to culture and industry through creativity"...
contains a geometric figure which is based on the stellation diagram of the icosahedron.
See also
- Truncated icosahedronTruncated icosahedronIn geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....
- Regular polyhedronRegular polyhedronA regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
- Geodesic gridGeodesic gridA geodesic grid is a technique used to model the surface of a sphere with a subdivided polyhedron, usually an icosahedron.-Introduction:...
s use an iteratively bisected icosahedron to generate grids on a sphere - Jessen's icosahedronJessen's icosahedronJessen's icosahedron, sometimes called Jessen's orthogonal icosahedron is a non-convex polyhedron with the same number of vertices, edges and faces as the regular icosahedron...
- Infinite skew polyhedronInfinite skew polyhedronIn geometry, an infinite skew polyhedron is an extension of the idea of a polyhedron, consisting of regular polygon faces with nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a closed surface....
- PseudoicosahedronPseudoicosahedronIn geometry, a pseudoicosahedron is a twelve-sided polyhedron that can be regarded as a particular form of distorted regular icosahedron containing tetrahedral symmetry...
External links
- Editable printable net of an icosahedron with interactive 3D view
- Paper models of the icosahedron
- The Uniform Polyhedra
- K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Interactive Icosahedron model - works right in your web browser
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Tulane.edu A discussion of viral structure and the icosahedron
- Paper Models of Polyhedra Many links
- Origami Polyhedra - Models made with Modular Origami
- Video of icosahedral mirror sculpture
- http://web.uct.ac.za/depts/mmi/stannard/virarch.html Principle of virus architecture




