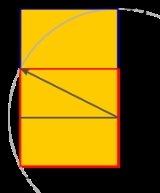
Golden rectangle
Encyclopedia
A golden rectangle is one whose side lengths are in the golden ratio
,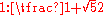 or approximately 1:1.618.
or approximately 1:1.618.
A distinctive feature of this shape is that when a square
section is removed, the remainder is another golden rectangle
; that is, with the same proportion
s as the first. Square removal can be repeated infinitely, in which case corresponding corners of the squares form an infinite sequence of points on the golden spiral
, the unique logarithmic spiral
with this property.
According to astrophysicist and math popularizer Mario Livio
, since the publication of Luca Pacioli
's Divina Proportione in 1509, when "with Pacioli's book, the Golden Ratio started to become available to artists in theoretical treatises that were not overly mathematical, that they could actually use," many artists and architects have been fascinated by the presumption that the golden rectangle is considered aesthetically pleasing. The proportions of the golden rectangle have been observed in works predating Pacioli's publication.
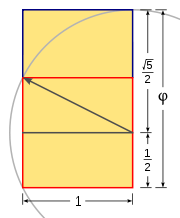 A golden rectangle can be constructed with only straightedge and compass by this technique:
A golden rectangle can be constructed with only straightedge and compass by this technique:
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
,
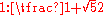 or approximately 1:1.618.
or approximately 1:1.618.A distinctive feature of this shape is that when a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
section is removed, the remainder is another golden rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
; that is, with the same proportion
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
s as the first. Square removal can be repeated infinitely, in which case corresponding corners of the squares form an infinite sequence of points on the golden spiral
Golden spiral
In geometry, a golden spiral is a logarithmic spiral whose growth factor is , the golden ratio. That is, a golden spiral gets wider by a factor of for every quarter turn it makes.-Formula:...
, the unique logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
with this property.
According to astrophysicist and math popularizer Mario Livio
Mario Livio
Mario Livio is an astrophysicist and an author of works that popularize science and mathematics. He is currently an astronomer and head of public outreach at the Space Telescope Science Institute, which operates the Hubble Space Telescope...
, since the publication of Luca Pacioli
Luca Pacioli
Fra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and seminal contributor to the field now known as accounting...
's Divina Proportione in 1509, when "with Pacioli's book, the Golden Ratio started to become available to artists in theoretical treatises that were not overly mathematical, that they could actually use," many artists and architects have been fascinated by the presumption that the golden rectangle is considered aesthetically pleasing. The proportions of the golden rectangle have been observed in works predating Pacioli's publication.
Construction

- Construct a simple square
- Draw a line from the midpoint of one side of the square to an opposite corner
- Use that line as the radius to draw an arc that defines the height of the rectangle
- Complete the golden rectangle
Applications
- Le CorbusierLe CorbusierCharles-Édouard Jeanneret, better known as Le Corbusier , was a Swiss-born French architect, designer, urbanist, writer and painter, famous for being one of the pioneers of what now is called modern architecture. He was born in Switzerland and became a French citizen in 1930...
's 1927 Villa SteinVilla SteinVilla Stein, designed by Le Corbusier, was built in 1927 at Garches, France. The building is also known as Villa Garches, Villa de Monzie, and Villa Stein-de Monzie. Located at 7 Rue de professeur Victor Pauchet, the villa was built for M. de Monzie and then sold to Gertrude Stein.- External...
in GarchesGarchesGarches is a commune in the western suburbs of Paris, France. It is located from the centre of Paris.Garches has remained largely residential, but is also the location of the Hôpital Raymond Poincaré , which specialises in traumatology, road accidents and physiotherapy.-19 January Monument:The...
features a rectangular ground plan, elevation, and inner structure that are closely approximate to golden rectangles. - The flag of TogoFlag of TogoThe flag of Togo was adopted on April 27, 1960. It has five equal horizontal bands of green alternating with yellow. There is a white five-pointed star on a red square in the upper hoist-side corner...
was designed to approximate a golden rectangle closely.
See also
- Fibonacci numbers
- Golden rhombus
- Kepler triangle
- Leonardo of Pisa
- Rabatment of the rectangleRabatment of the rectangleRabatment of the rectangle is a compositional technique used as an aid for the placement of objects or the division of space within a rectangular frame, or as an aid for the study of art....
- Silver ratioSilver ratioIn mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,...
External links
- Golden Ratio at MathWorld
- The Golden Mean and the Physics of Aesthetics
- Golden rectangle demonstration With interactive animation

